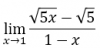-
Mateo Arízaga
el 21/10/16Buenas noches, alguien que me ayude con estos ejercicios, de antemano gracias :3
Antonio Silvio Palmitano
el 21/10/16a) Observa que para t = 0 corresponde el punto de coordenadas A(-1,0), y para t = 4 corresponde el punto de coordenadas B(11,4).
Luego, despejas t en ambas ecuaciones paramétricas, igualas y queda la ecuación cartesiana:
y = (x - 4)/3, distribuyes el denominador a la derecha:
y = (1/3)x - 4/3, que es la ecuación cartesiana explícita de una recta en el plano,
por lo que concluimos que la trayectoria es un segmento de esta recta, con primer punto A y último punto B.
b) Observa que para t = -3 corresponde el punto de coordenadas A(-15,5), y para t = 3 corresponde el punto de coordenadas B(15,5).
Luego, observa que puedes factorizar la expresión para x:
x = t(t^2 - 4), y luego susituir en ella la expresion para y, y por el momento queda:
x = ty (*).
Luego, observa la expresión para y: su gráfica en un sistema cartesiano t-x es un trazo de parábola, y observa que y toma valores positivos en el intervalo [-3,-2) u (2,3], valores negativos en el intervalo (-2,2), y toma el valor 0 para x = -2 y x = 2. Observa también que para t = -2 corresponde el punto C(0,0), y que para t = 2 también corresponde el punto C(0,0) (observa que la gráfica se corta a sí misma en el punto C(0,0)).
Luego despejamos t en esta expresión y nos queda en dos trozos:
t = +V(y + 4)
t = -V(y + 4)
Luego, sustituimos en la expresión señalada y nos quedan dos trozos:
x = yV(y +4), para los puntos que correspondan al los valores de t del primer intervalo,
x = -yV(y +4), para los puntos que correspondan a los valores de t del segundo intervalo.
Luego observa que si elevamos al cuadrado en ambos miembros, obtenemos una única ecuación:
x^2 = y^2 * (y + 4).
Con respecto a su gráfica, deberás apelar a un programa informático.
c) Observa que para t = 2 corresponde el punto de coordenadas A( 0 ,3V(2) ), y que para t = 4 corresponde el punto de coordenadas B( 2V(2) , 0 ).
Observa también que, de acuerdo con las expresiones paramétricas, tanto x como y toman valores positivos, por lo que la curva se encuentra en el primer cuadrante (*).
Luego, despejamos t en ambas expresiones paramétricas:
t = x^2 / 4 + 2
t = 4 - y^2 / 9
luego igualamos y queda:
x^2 / 4 + 2 = 4 - y^2 / 9
luego hacemos pasajes de términos, reducimos términos numéricos y queda:
x^2 / 4 + y^2 / 9 = 2
luego dividimos por 2 en todos los términos y tenemos:
x^2 / 8 + y^2 / 18 = 1
que es la ecuación cartesiana canónica de una elipse con centro de simetría C(0,0), semieje mayor sobre el eje OY cuya longitud es a = V(18), y semieje menor sobre el eje OX cuya longitud es b = V(8).
Por último, concluimos, a partir de la consideración señalada (*), que la curva es el arco de esta elipse que se encuentra en el primer cuadrante.
Espero haberte ayudado.
-
miky
el 21/10/16Por fa amigos me echarían una ayudita con estos 2 ejercicios.
.
-
Alex Rojas
el 21/10/16 -
Keith Caballero Rodriguez
el 20/10/16Buenas quisiera hacer una consulta , quisiera saber cual es la diferencia de probar que exista un subespacio con la prosición 3 o con la proposición 2, por favor resuelvan mis dudas.
Antonius Benedictus
el 20/10/16No hay diferencia, Keith. Son proposiciones equivalentes. En el fondo, con más o menos concisión, todo se reduce a una idea muy sencilla:
Un subconjunto U de un espacio vectorial V es un subespacio vectorial cuando se reproducen en él las propiedades de un espacio vectorial Lo cual viene a decir que: CUALQUIER COMBINACIÓN LINEAL DE ELEMENTOS de U también pertenece a U.
-
Lorena Llanos
el 20/10/16 -
Ángel
el 20/10/16 -
Matias
el 20/10/16Hola Unicoos! me pueden ayudar con este ejercicio? No entiendo que tengo que plantear en la segunda parte del ejercicio ni lo que es gen(u).
Muchas gracias y saludos!
Antonius Benedictus
el 20/10/16 -
:)
el 20/10/16tengo dudas cone ste ejercicio de matematica no entendi bien
p(x)=-3x^3+ax^2-4x+5
1)p(x) es dividido X+3 da resto -5
2) -2 es raiz de p(x)
3) p(-3)=-1
Antonio Silvio Palmitano
el 20/10/161) Puedes aplicar el Teorema del Resto: R = P(a), cuando el divisor es (x- a), y para este ejercicio tienes:
P(-3): - 3(-3)^3 + a(-3)^2 - 4(-3) + 5 = - 5, resolvemos términos:
81 + 9a + 12 + 5 = - 5, hacemos pasajes de términos y resolvemos a la derecha:
9a = -103, hacemos pasaje de factor como divisor:
a = - 103/9.
2) Tenemos, como -2 es raíz de P(x), que el resto es igual a cero, aplicamos el Teorema y tenemos:
P(-2): - 3(-2)^3 + a(-2)^2 -4(-2) + 5 = 0, resolvemos términos:
24 +4a + 8 + 5 = 0, reducimos términos semejantes:
4a + 37 = 0, hacemos pasaje de término, y luego pasaje de factor como divisor y queda:
a = - 37/4.
3) Evaluamos la expresión de P(x):
P(-3): - 3(-3)^3 + a(-3)^2 - 4(-3) + 5 = - 1, resolvemos términos:
81 + 9a + 12 + 5 = - 1, hacemos pasajes de términos y resolvemos a la derecha:
9a = - 99, hacemos pasaje de factor como divisor:
a = - 99/9 = -11.
Observa que son tres ejercicios distintos.
Espero haberte ayudado.
-
Claudia Mullor
el 20/10/16Tengo una duda, bueno bastantes la verdad y he estado buscando vídeos y no se si es que no hay o no los encuentro, y a ver, he dado los radicales y no sé cómo se racionaliza por ejemplo: (√a-√b)÷√ab
Y tampoco entiendo como se hace el teorema del resto y el teorema del factor
Jordi García
el 20/10/16Mírate estos vídeos:
Racionalizar: http://www.unicoos.com/leccion/matematicas/4-eso/numeros-reales/radicales
Teorema del resto: http://www.unicoos.com/leccion/matematicas/4-eso/polinomios/teorema-del-resto
Teorema del factor: https://www.youtube.com/watch?v=5sK6udxDNWI
o http://www.ditutor.com/polinomios/teorema_factor.html
Saludos
-
Jordi García
el 20/10/16
Hola UNICOOS, tengo la siguiente duda:
¿Cuál es el criterio de divisibilidad de la tabla del 2 en base 9?
Por ejemplo, ¿cómo sabemos si el número 311 es divisible por 2 en base 9?
Gracias.
