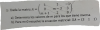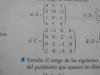-
andrea
el 17/10/16hola, tenía dos preguntas:
1)un ejercicio de racionalizar y simplificarlo: 1+raiz cuadrada de x dividido entre raiz cubica de x elevado al cuadrado.paso a paso por favor
y el 2) ejercicio dice así: ¿cuánto tiempo hay que depositar 3000€ al 4% de interés para tripicarlo? responde según sea interes simple o compuesto.
Muchas gracias.Un saludo
Antonio Silvio Palmitano
el 17/10/161) Si la expresión es: ( 1 + V(x) ) / (3V)(x^2) = multiplicamos y dividimos por (3V)(x):
= ( 1 + V(x) )*(3V)(x) / ( (3V)(x^2)*(3V)(x) ) = asociamos raíces entre los factores del denominador =
= ( 1 + V(x) )*(3V)(x) / ( (3V)(x^3) ) = simplificamos raíz y potencia en el denominador = ( 1 + V(x) )*(3V)(x) / x.
2) Faltan datos: no se enuncia el periodo de capitalización (anual, semestral, mensual,...).
Espero haberte ayudado.
-
Bea Salvador Herrerin
el 17/10/16 -
Joship
el 17/10/16hola Unicoos me podrían hechar una mano con esto dos ejercicios por favor no me salen
Antonio Silvio Palmitano
el 17/10/16Problema 5. Observa que:
El primer día se fabrica (3/8)R, y falta fabricar (5/8)R.
El segundo día se fabrica (3/10)(5/8)R = (3/16)R, ya se fabricó (3/8 + 3/16)R = (9/16)R, y falta fabricar (7/16)R.
El tercer día se fabrica (1/5)(7/16)R = (7/80)R, ya se fabricó (9/16 + 7/80)R = (13/20)R, y falta fabricar (7/20)R.
El cuarto día se fabrica (7/20)R = 168 paquetes (*) y el trabajo está completo.
Luego, a partir de la ecuación señalada (*) despejamos y queda:
x = 168 / (7/20) = 480 paquetes.
6) Tenemos en cada línea:
L2 = 3 = 3^1
L3 = 9 = 3^2
L4 = 27 = 3^3
L5 = 81 = 3^4
L6 = 243 = 3^5.
Luego la cantidad total de personas será L2 + L3 + L4 + L5 + L6 = L, luego tenemos (extraemos factor común 3):
L = 3*(1 + 3 + 3^2 + 3^3 + 3^4),
observa que tenemos una prograsión geométrica de razón 3 en el agrupamiento, con exponentes desde 0 hasta 4, evaluamos (recurre a tus apuntes) y queda:
L = 3 * (1 - 3^5)/(1 - 3), resolvemos potencias en el numerador y resolvemos el denominador:
L = 3*(1 - 243)/(-2), resolvemos el agrupamiento en el numerador:
L = 3*(- 242)/(-2), resolvemos y llegamos a:
L = 363 personas recibieron el mensaje enviado por el emisor.
Verificamos:
L = 3 + 9 + 27 + 81 + 243 = 363.
Espero haberte ayudado.
-
Richard
el 17/10/16 -
dovigame
el 17/10/16Buenas tardes únicos por favor necesito vuestra ayuda con este problema.Dice así :halla el área del recinto limitado por la parábola y^2=4-x a la recta x=0
Antonio Silvio Palmitano
el 17/10/16Puedes integrar con respecto a y, y representar las curvas en un sistema cartesiano "invertido" con eje horizontal y, y con eje vertical x.
Las ecuaciones de las curvas quedan:
x = 4 - y^2 (parábola, con vértice en el 4 del eje vertical, que corta al eje horizontal en -2 y en 2)
x = 0 (eje horizontal).
Luego, el área queda planteada con la integral:
A = Integral ( (4 - y^2) - 0 )*dy = [ 4y - (1/3)*y^3 ] = evaluamos con regla de Barrow entre -2 y 2 = (8 - 8/3) - (- 8 + 8/3) = 32/3.
Espero haberte ayudado.
-
Gabriela
el 17/10/16 -
Alejandro Ballesteros
el 17/10/16Hola buenas por favor calculen el rango del C desarrollando por la primera COLUMNA. Muchas gracias
David
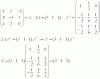
el 18/10/16Resta a la cuarta fila la primera fila (F4=F4-F1)... Te quedará...
(2 -1 0 0)
(0 0 2 -1)
(0 2 -1 0)
(0 1 -1 0)
Cambia la fila 2 por la 4 y la fila 4 por la 3 ...
(2 -1 0 0)
(0 1 -1 0)
(0 0 2 -1)
(0 2 -1 0)
Resta a la cuarta fila la segunda por 2 (F4=F4-2F2)
(2 -1 0 0)
(0 1 -1 0)
(0 0 2 -1)
(0 0 1 0)
El rango es 4 -
Marina
el 17/10/16Hola Unicoos no tengo ni idea de este problema:
Pepe le pregunta a Juan su edad y este le contesta:
-Cuando yo nací, y no me acuerdo el año, mi unica hermana tenia solo un quarto de edad que mi madre tiene actualmente y ahora tiene un tercio de edad de mi padre.
Ahora yo solo tengo un quarto de edad de mi madre y de aqui a quatro años tendré la quarta parte de edad que mi padre tiene actualmente.
-
lbp_14
el 17/10/16 -
Alex Rodriguez
el 17/10/16Buenas Unicoos!! :)
Gracias por sus vídeos siempre me ayudaron en todo! ☺Una pregunta, algún libro que me recomienden para aprender a comprender y resolver problemas matemáticos?
Siempre me costaron los problemas matemáticos, siempre intento leerlo muchas veces pero no me llegan a salir y peor aun los Problemas Fraccionarios :( (Y Sí.. se resolver fracciones... )
Jordi García
el 17/10/16
