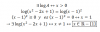-
Buenos días:
Agradeceré me ayuden con el siguiente ejercicio de 1ro de Bachillerato Ciencias
determina para qué valores de x es posible realizar la siguiente operación: log (x^2 - 2^x + 1).
Un saludo,
Gustavo
-
Hola queridos amigos de unicoos, alguien me puede ayudar con la siguie te ecuación...
3^(x-3)=54(x-3)
3(x-3)=54(x-3)
En el miembro es una potencial... en el segundo no
Gracias de antemano
-
¿Me ayudan con este ejercicio?
Dada f(x)= √(1+x)
a) Calcular el polinomio de Taylor en el cero (Mac-Laurin) de
grado 4b) Utilizarlo para aproximar el valor de √1.02 acotando el error
cometido en dicha aproximación.Saludos y gracias
-


Antonio Silvio Palmitano
el 17/10/16Debes plantear equivalencias lógicas (indicamos pertenece con p, no pertenece con np, conjunción con y, disyunción con o).
x p (A - C) u (B - C) <--> (definición de unión)
<--> x p (A - C) o x p (B - C) <--> (definición de diferencia)
<--> ( (x p A) y (x np C) ) o ( (x p B) y (x np C) ) <--> (factor común)
<-- > ( (x p A) o (x p B) ) y (x np C) <--> (definición de unión)
<--> ( x p (A u B) ) y (x np C) <--> (definición de diferencia)
<--> x p ( (A u B) - C ).
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/10/16Observa que podemos escribir la proposición en la forma: P(n): n^3 - n = 3t, con t perteneciente a N, luego probaremos por Inducción Completa:
P(0): 0^3 - 0 = 0 = 3*0, es Verdadera.
Hipótesis Inductiva, P(h): h^3 - h = 3*t1, con t1 perteneciente a N, que aceptamos como Verdadera.
Tesis Inductiva, P(h+1): (h+1)^3 - (h+1) = 3*t2, con t2 perteneciente a N, que tenemos que probar que es Verdadera.
Demostración:
(h+1)^3 - (h+1) = desarrollamos y distribuimos = h^3 + 3h^2 + 3h + 1 - h - 1 = reducimos términos semejantes, ordenamos y asociamos términos:
= ( h^3 - h ) + 3h^2 + 3h = aplicamos la Hipótesis Inductiva (observa el agrupamiento de términos).
= 3*t1 + 3h^2 + 3h = extraemos factor común:
= 3*(t1 + h^2 + h) = 3*t2,
observa que t2 pertenece a N por ser el producto de un número natural (3) por la suma de tres números naturales: t1 (de la Hipótesis Inductiva), h^2 y h.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 17/10/16Vas bien en toda tu primera línea, luego, multiplica y divide por cosx, y queda:
I = (1/2) * Integral ( 1 / ( (senx)^2 * (cosx)^2 ) ) * cosx*dx = por identidad trigonométrica =
= (1/2) * Integral ( 1 / ( (senx)^2 * ( 1 - (senx)^2 )) * cosx*dx,
luego puedes plantear la sustitución (cambio de variable):
w = senx, de donde tienes: dw = cosx*dx, luego sustituyes y queda:
I = (1/2) * Integral ( 1 / ( w^2 * (1 - w^2) ) )* dw,
que puedes resolver con el método de las fracciones parciales. Haz el intento de terminar el ejercicio y, si es preciso, vuelves a consultar.
Espero haberte ayudado.
-
Tengo esta duda:
El problema dice :
Encuentre la recta tangente a la gráfica de la función dada
x= t^2 -4t-2
y=t^5-4t^2-1
sacar la pendiente ya se como se hace pero me pidieron que sacara todas las rectas tangentes HORIZONTALES de la gráfica y cuales son esos puntos donde pasan la rectas me podrían ayudar por favor :) se los agradecería


Joaquin Garay
el 17/10/16Ya entonces las rectas tangentes horizontales son cuando la derivada de la funcion es igual a 0. Fijate primero que la funcion en x es una parabola horizontal, entonces creo que su recta tangente nunca será horizontal. La funcion definida para y sería:
y' = 5t^4-8t = 0 t(5t^3-8)=0 t=0 y t=³√(8/5) en esos puntos la recta tangente es horizontal. No estoy seguro pero creo q sería la respuesta.

Antonio Silvio Palmitano
el 17/10/16Observa que tienes las ecuaciones cartesianas paramétricas de una curva, por lo que podemos plantear:
y ' = dy/dx = (dy/dt) / (dx/dt) = 0 (observa que nos piden rectas tangentes horizontales.
Luego hacemos pasaje de divisor como factor en la última igualdad de la cadena (observa que debe verificarse que dx/dt sea distinto de cero), resolvemos a la derecha y queda:
dy/dt = 0, derivamos la expresión y, reemplazamos y queda:
5t^4 - 8t = 0, observa que al derivar la expresión x, tenemos la condición: 2t - 4 distinto de cero(*), factorizamos y queda:
t(5t^3 - 8) = 0, que nos conduce a dos opciones:
1) t = 0, que nos conduce al punto de coordenadas P1(-2,-1)
2) t = (3V)(8/5), que puedes reemplazar en las expresiones de x e y para encontrar las coordenadas del punto,
observa que la condición señalada (*) se cumple para ambos valores de t.
Espero haberte ayudado.
-
Hola a todos, hace unos dias puse unos ejercicios de espacios vectoriales y me quedo una duda, cual es la forma de saber si determinados vectores son un sistema de generadores o no?
Gracias!