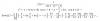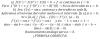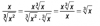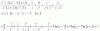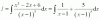-
Tatiana
el 10/10/16 -
Lau
el 10/10/16Hola alguien podría decirme si está bien hecha esta notación científica, muchas gracias
Matías Ignacio Loyola Galdames
el 10/10/16Si hiciste bien los cálculos en la calculadora y llegaste a esto: 712,72...
Para dejarlo en notación científica, tienes que dejar un número entre 1 y 10(sin incluir el 10) por diez elevado a la potencia correcta.
Y como te piden con 3 cifras significativas, primera deja el número que te dio con 3 cifras significativas, te queda 713 (por la aproximación)
y ahora lo transformas a notación científica a 7,13 x 10 elevado a 2.
No sé si fui claro.
-
Carla
el 10/10/16Hola, les quería pedir si me podían ayudar con la (b) del problema 1, muchas gracias.
Antonio Silvio Palmitano
el 10/10/16Debes tener en cuenta la desigualdad: |senu| <= u, para todo u perteneciente a R (*);
la identidad trigonmétrica: sena - senb = 2*sen((a-b)/2)*cos((a+b)/2) (**);
la propiedad del valor absoluto: |u*v| = |u|*|v| (***);
y la propiedad: |cosw| <= 1 (****).
Luego tenemos:
|sena - senb| = por identidad (**) = |2*sen((a-b)/2)*cos((a+b)/2)| = por propiedad (***) = 2*|sen((a-b)/2|*|cos((a+b)/2)| <= por propiedad (*):
< = 2*|a-b|/2 * |cos((a+b)/2)| = simplificamos = |a-b|*|cos((a+b)/2)| <= por propiedad (****) <= |a-b|*1 = |a-b|.
Por lo que hemos probado que la inecuación es verdadera.
Espero haberte ayudado.
-
Majda Yahya
el 10/10/16Hola buenas tardes me gustaría saber porque se ha multiplicado por la raíz tercera pero la x no esta elevada al cuadrado.
-
Celia Garrido
el 10/10/16 -
Genesis Guzman
el 10/10/16 -
Genesis Guzman
el 10/10/16 -
Natalia Jacob
el 10/10/16Hola!!
Disculpen, Alguien que me pueda ayudar con 2 ejercicios.
Sea f:R^2--R la función definida por f(x,y)=|x|+2|y| encuentre la preimagen de 2 bajo f ?
Por favor.
Antonio Silvio Palmitano
el 10/10/16Comencemo por plantear: f(x,y) = 2, luego sustituimos la expresión de la función y queda:
|x| + 2|y| = 2.
Luego, observa que tenemos cuatro casos, según la definición de valor absoluto:
1) x >= 0, y >= 0, x + 2y = 2, que al graficar queda un segmento recto en el primer cuadrante, con extremos: (2,0) y (0,1).
2) x >= 0, y < 0, x - 2y = 2, que al graficar queda un segmento recto en el cuarto cuadrante, con extremos (2,0) abierto y (0,-1).
3) x < 0, y >= 0, -x + 2y = 2, que al graficar queda un segmento de recta en el segundo cuadrante, con extremos (-2,0) abierto y (0,1).
4) x < 0, y < 0, -x - 2y = 2, que al graficar queda un segmento de recta en el tercer cuadrante, con extremos abiertos (-2,0) y (0,-1).
Luego, el gráfico de la preimagen de 2 es un rombo con centro de simetría en el origen, y ejes de simetría coincidentes con los ejes coordenados.
Espero haberte ayudado.
-
David Anguita
el 10/10/16Hola tengo una duda con el ejercicio que realizas en el video de combinatoria (permutaciones con repetición), bueno con una pequeña variación: si en las cifras que nos dan para formar el número de 9 cifras hubiese algún número que no se repitiese, se resolveria de la misma manera? por ejemplo: 2,2,2,3,3,3,3,3,4 : ??? Es decir, (9! / 3!·5!·1!)
Y si hubiesen 2 números sin repetición junto a 2 con repetició? 2,2,2,2,3,3,3,4,5
Gracias y un saludo!
Nico
el 10/10/16Hola David, por suerte este ejercicio es sencillo pero los problemas de combinatoria pueden llegar a ser un gran dolor de cabeza... en estos ejercicios siempre se divide por la cantidad de veces factorial que se repite el numero , en el caso que mencionas por ejemplo seria asi: 2,2,2,2, 3,3,3,, 4, 5 : 9!/4!3!
-
Fermat
el 10/10/16Imposible llegar a esta solución. [Último determinante, lo juro :)]. Muchas Gracias!
