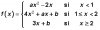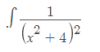-
-


Antonio Silvio Palmitano
el 10/10/16Puedes plantear la sustitución: x = 2tant, de donde tienes:
dx = ( 2 / (cost)^2 )*dt, y también tienes:
x^2 + 4 = 4*(tant)^2 + 4 = 4*( 1 + (tant)^2 ) = 4 / (cost)^2.
Luego sustituyes en la expresión de la función y queda:
1 / (x^2 + 4)^2 = 1 / ( 16 / (cost)^4 ) = (cost)^4 / 16.
Luego, la integral queda:
I = Integral ( (cost)^4 / 16 )* ( 2 / (cost)^2 )*dt = (1/8)*Integral ((cost)^2)*dt.
Luego, como seguramente has visto en clase, aplicas la identidad trigonométrica: (cost)^2 = 1/2 + (1/2)cos(2t) para resolver la integral.
Te recomiendo mires los vídeos.
Espero haberte ayudado.
-
No sé como afrontar estos ejercicios. Gracias de antemano.
Se suelen usar contraejemplos y reducción al absurdo pero no se realmente aplicarlo.


Antonio Silvio Palmitano
el 10/10/16Debes recordar propiedades del valor absoluto: u <= |u|, y |-u| = |u|, u^2 = |u|^2 y también |uv| = |u||v|.
Para el ejercicio a:
Probaremos que : |x+y|^2 <= ( |x|+|y| )^2:
|x+y|^2 = tercera propiedad = (x+y)^2 = x^2 + 2xy + y^2 = tercera propiedad = |x|^2 + 2xy + |y|^2 <= primera propiedad <= |x|^2 + |2xy| +|y|^2 = cuarta propiedad = |x|^2 + 2|x||y| + |y|^2 = (|x|+|y|)^2.
Luego, a partir de la cadena de igualdades y desigualdades tenemos que:
|x+y|^2 <= (|x|+|y|)^2, extraemos raíz cuadrada en ambos miembros (observa que los argumentos de los cuadrados son positivos) y queda:
|x+y| <= |x|+|y|, que es conocida como Desigualdad Triangular (DT).
En el ejercicio b:
|x| = |(x-y) + y| <= DT <= |x-y| + |y|.
Luego, a partir de la cadena de igualdad y desigualdad tenemos que:
|x| <= |x-y| + |y|, luego hacemos pasaje de término y queda:
|x| - |y| <= |x-y|, luego escribimos según se lee de derecha a izquierda y llegamos a:
|x-y| >= |x| - |y|.
En el ejercicio c:
|y| - |x| = |(y-x)+ x| - |x| <= DT <= |y-x| + |x| - |x| = cancelamos términos opuestos = |y-x| = segunda propiedad = |-1(x-y)| = cuarta propiedad = |-1||x-y| = =1|x-y| = |x-y|.
Luego, a partir de la cadena de igualdades y desigualdades tenemos que:
|y| - |x| <= |x-y|, luego escribimos la desigualdad según se lee de derecha a izquierda y llegamos a:
|x-y| >= |y| - |x|.
En el ejercicio d:
Puedes partir de la inecuación que hemos probado en el ejercicio b:
|x-y| >= |x| - |y|
Escribimos la desigualdad según se lee de dercha a izquierda y tenemos:
|x| - |y| <= |x-y|, luego haces pasaje de término y llegas a:
|x| <0 |x-y| + |y|.
Espero haberte ayudado.
-
Probar que si 0<a<b, entonces a2<b2
Si elevo al cuadrado la expresión de partida 02<a2<b2 , pero ¿Queda probado así?
Gracias.


Aleking
el 10/10/16Claro. Si suponemos que b2 < a2 llegamos a esa conclusión según el razonamiento seguido. Y está en contradicción con la hipótesis de la que partíamos, que decía que a < b. En eso se basa la reducción al absurdo, suponer lo contrario de lo que se quiere demostrar y concluir que se contradice con la hipótesis inicial, ya que no puede ser a < b y b < a a la vez y, por lo tanto, la suposición inicial de que b2 < a2 debe ser falsa. No sé si me he explicado.


David
el 10/10/16Si que logro entenderte (creo). Pero me refiero, busca un contraejemplo que anule la afirmación del enunciado. Yo creo que es correcto lo que dice el enunciado.
Si partes de que b2 < a2 entonces b < a, y si partes de lo contrario entonces a < b. No?
Creo que este ejercicio se tiene que enfocar más por el tema de valores absolutos, ya que al ser 0>a, y a>b estamos siempre hablando de valores positivos. Entonces se deduce que para valores positivos se cumple: No se si queda así probado, si se hace así o cómo. JEJE


Aleking
el 10/10/16El enunciado claro que es correcto y, por tanto, es imposible encontrar un contraejemplo que lo anule. Sin embargo, hay que probar que efectivamente es correcto. ¿Cómo se hace? Hemos usado la técnica de reducción al absurdo, de forma que, si suponemos que b2< a2 ¡y aplicando por el camino que a < b! llegamos a la conclusión de que b < a. Esto es una contradicción y no tiene sentido. ¿A qué se debe entonces? A que hemos partido de algo falso, es decir, que no es posible que b2 < a2. Esta es la base de la demostración por reducción al absurdo.
Si partimos de lo contrario, como sugieres, aunque llegáramos a la conclusión de que a < b, no tenemos la demostración que queríamos, pues la nuestra iba en el otro sentido (al revés).
En cuanto a la imagen que muestras, fíjate que en el primer paso estás dando por supuesto lo que quieres demostrar... Eso sí, muy bien que te hayas dado cuenta de la observación que haces en la última línea (eso demuestra que eres bueno ;)


Aleking
el 10/10/16Espero que realmente te haya quedado claro. De todas formas, cuando hayas utilizado en más ocasiones la técnica de reducción al absurdo, seguramente lo verás todo mucho más claro. Al principio puede parecer un poco extraño, pero al final te acostumbras, jajaja.
Te recomendaría que lo pensaras detenidamente hasta que no te queden dudas. Un saludo.


Aleking
el 11/10/16Existen muchas demostraciones que se basan en la reducción al absurdo, pero hay una muy bonita, que quizá no sea la más fácil de ver al principio. Se trata de la demostración de que la raíz de dos es un número irracional. En Internet aparece en bastantes sitios.
Prueba a ver si la entiendes, es muy ingeniosa.
-


Antonio Silvio Palmitano
el 10/10/16De acuerdo con el colega Matías, el denominador queda factorizado: (x-1)^2 * (x+1). Luego, descomponemos como suma de fracciones parciales, extraemos denominador común y el numerador queda:
A(x+1) + B(x-1)(x+1) + C(x-1)^2 = x + 2.
Luego evaluamos para tres valores distintos de x:
para x=1 queda: 2A = 3, de donde tienes: A = 3/2;
para x = -1 queda: 4C = 1, de donde tienes: C = 1/4;
para x=0 queda: A - B + C = 2, despejas, reemplazas y tienes: 3/2 + 1/4 - 2 = B, resuelves y llegas a: -1/4 = B.
Luego puedes continuar la tarea (observa que te quedan tres integrales sencillas que se resuelven con sustituciones).
Espero haberte ayudado.
-
Buenas unicoos, quisiera saber si este ejercicio eata bien resuelto, mi duda mas que todo es en la altura (h) del trigulo ABC, esta.bien planteado respeto a la altura (CE)?. La repuesta del ejercicio es la opcion e) ninguna de las anteriores. Muchas gracias





Antonio Silvio Palmitano
el 10/10/16Por lo que se entiende de tu dibujo, el vértice D corresponde a un ángulo recto, y el dato es: |AD| = V(3).
Luego, vamos al triángulo rectángulo ADB, y para él planteamos: tan30° = |AD|/|BD|, reemplazamos valores y queda:
V(3)/3 = V(3)/|BD|, luego despejas y queda: |BD| = 3.
Luego, el área del triángulo rectángulo ADB es: A1 = |BD|*|AD|/2 = 3*V(3)/2.
Luego vamos al triángulo rectángulo ADC (donde C es vértice del ángulo de 60°), y para él planteamos: tan60° = |AD|/|BC|, reemplazamos valores y queda:
V(3) = V(3)/|BC|, luego despejas y queda: |BC| = 1.
Luego el área del triángulo rectángulo ADC es: A2 = |BC|*|AD|/2 = 1*V(3)/2.
Por último, planteamos el área del triángulo oblicuo ABC como diferencia entre las dos áreas anteriores y llegamos a:
A = A1 - A2 = 3*V(3)72 - 1*V(3)/2 = 2*V(3)/2 = V(3).
Espero haberte ayudado.
-
Tengo en una duda en este ejercicio, nose si hice algo mal cuando descompuse la expresion porque A y B no me da un valor a la x



Antonio Silvio Palmitano
el 10/10/16Observa que la expresión a integrar queda, una vez factorizado su denominador: 7 / (2x+1)^2, = 7 * (2x+1)^(-2).
Luego, la integral queda:
I = Integral ( 7 * (2x+1)^(-2) )*dx = 7 * Integral ( (2x+1)^(-2) )*dx, que puedes resolver por medio de la sustitución (cambio de variable): w = 2x+1.
Observa que en este caso no es necesario aplicar el método de las fracciones parciales.
Espero haberte ayudado.