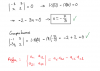Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Yiyi
el 9/10/16

Buenas tardes, me ayudan a resolver el problema 16 de ecuaciones diferenciales por favor, pensé en calcular las raíces según el tipo de solución, para luego formar el polinomio, pero tuve problema con el 2x-2. Hay alguna otra forma?

••0 voto/s
•
David
el 10/10/16
Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. Lo siento de corazón… Espero lo entiendas

•0 voto/s
•

Cancelar
Cristina
el 9/10/16

Hola ¿me podeis ayudar con este problema? Gracias!

••0 voto/s
•
David
el 10/10/16
(4 3)
(5 4)
(L3 L4 L5).(6 5)= (V1 V2) es la matriz que te indica el numero de ventanas grandes y pequeñas. El resultado es una matriz 1x2

El numero de cristales será...
(2)
(V1 V2).(4)

El numero de bisagras será...
(4)
(V1 V2).(6)

El numero de cristales y bisagras será
(2 4)
(V1 V2).(4 6)

•1 voto/s
•

Cancelar
Fermat
el 9/10/16

^{Hola muy buenas, no consigo resolver este determinante igualado a cero. Ayuda!}

••0 voto/s
•
Antonius Benedictus
el 9/10/16
Te lo explicamos, Fermaz:

•1 voto/s
•
Fermat
el 9/10/16
Mil gracias Antonio!

•0 voto/s
•

Cancelar
Genesis Guzman
el 9/10/16

Queria saber si realice bien esta integral

••0 voto/s
•
Antonius Benedictus
el 9/10/16
¡Perfecta!

•0 voto/s
•
Frank Rios
el 9/10/16
La solución de usted es correcta

•0 voto/s
•
Genesis Guzman
el 9/10/16
Mi duda es que si se puede hacer de otra manera, osea ir dividiendo cada termine del numerador con la expresión del denominador...

•0 voto/s
•

Cancelar
The punk
el 9/10/16

Hola estoy repasando polinomios y no recuerdo como resolver este ejercicio me podrian ayudar

••0 voto/s
•
Antonius Benedictus
el 9/10/16
Te lo explicamos:

•0 voto/s
•

Cancelar
Robert
el 9/10/16

Hola unicoos. me pueden ayudar por favor con la siguiente cuestión. Gracias.

••0 voto/s
•
Antonius Benedictus
el 9/10/16
Te ayudamos, Robert:

•1 voto/s
•

Cancelar
Usuario eliminado
el 9/10/16

Hola la duda es si el ejercicio esta bien , pero la duda es suma inferior o superior para mi son ambas , gracias por su ayuda

••0 voto/s
•
Antonius Benedictus
el 9/10/16
Es x_0 =3
Los elementos de la partición son de la forma: 3+(i·3/n)
Se trata de una suma inferior de Darboux, pues en cada subintervalo se toma el valor mínimo de la función.

•0 voto/s
•

Cancelar
Lorena
el 9/10/16

¡Hola!
¿Alguien me podría ayudar a resolver estas ecuaciones con determinantes?

••0 voto/s
•
David
el 9/10/16
Es simplemente aplicar la regla de Sarrus, te resuelvo el primero. Ánimos con los otros. Si quieres compruébalos para asegurar el resultado:

•0 voto/s
•
Antonius Benedictus
el 9/10/16
Te resolvemos dos, Lorena. Haz tú las otras.

•1 voto/s
•

Cancelar
Lorena
el 9/10/16

¡Hola!
¿Alguien me podría ayudar a resolver estas ecuaciones con determinantes?

••0 voto/s
•
Antonio Silvio Palmitano
el 9/10/16
Recuerda cómo se desarrolla un determinante de dos filas y dos columnas: debes multiplicar los elementos de la diagonal principal, y restarle lo que obtienes al multiplicar la diagonal secundaria.
a) -1*2 - 3*x = 0. luego resuelves en el primer término y queda:
- 2 - 3*x = 0, haces pasaje de término y queda:
-3 * x = 2, divides en ambos miembros por -3 y llegas a:
x = -2/3.
En todos los demás ejercicios debes aplicar el mismo procedimiento. Vamos con el último:
d) (2-x)*(11+x) - 3*(5-x) = 0, distribuyes en ambos términos a la izquierda y queda:
22 + 2x - 11x - x^2 - 15 + 3x = 0, reduces términos semejantes y queda:
- x^2 - 6x + 7 = 0, multiplicas en todos los términos por -1 y queda:
x^2 + 6x - 7 = 0, aplicas la fórmula resolvente para ecuaciones polinómicas cuadráticas y tienes dos soluciones:
x1 = -7
x2 = 1.
Queda para que resuelvas los demás ejercicios.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
David
el 9/10/16

A ver si alguien me puede ayudar y explicarme por que la primera opción no es valida o qué estoy haciendo mal. Gracias.

••0 voto/s
•
Antonius Benedictus
el 9/10/16
David, te mando las fórmulas que debes utilizar para estas inecuaciones:

•1 voto/s
•
David
el 9/10/16
Es decir toma el mismo significado que el valor absoluto, ¿Correcto? Gracias

•0 voto/s
•
Aleking
el 9/10/16

•1 voto/s
•
Antonius Benedictus
el 9/10/16
Algo similar, David. Pero me vas a disculpar, pues se me olvidó colocarles a las r la raíz cuadrada. Te mando la versión corregida.

•1 voto/s
•

Cancelar