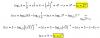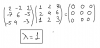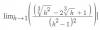-
Lucía
el 9/10/16Hola, en el ejercicio 2 no se como calcular por defecto y exceso y en el 4 como se puede hacer de un solo número? No necesitaría más de uno para tener a^2 y b^2?
-
Daniel
el 9/10/16 -
Angel
el 9/10/16 -
María
el 9/10/16¿Alguien me podría ayudar por favor? Me gustaría saber si he resuelto bien el apartado a, para poder seguir con el b. Gracias de antemano
David
el 9/10/16Hola María, es sencillo. Lo único que tienes que hacer es comprobar que es correcto y que A·B=0 (Siendo 0 la matriz nula de orden 3).
Recordarte que no se cumple la propiedad conmutativa en el producto de matrices, por lo tanto es muy importante multiplicar A·B y NO B·A.
Enhorabuena puedes seguir con el siguiente apartado.
-
María José Ledesma
el 9/10/16Hallar a y b > 00 tales que el límite dela función (cundo x tiende a infinito) de (√(ax^4 + bx^3)/x) - x =4
Resolviendo llegué a:
lim(x-->inf) = (ax^4 + bx - x^4)/(√(ax^4+bx) + x^3) = 4
Pero no sé como seguir para hallar los valores de a y b!
Antonio Silvio Palmitano
el 9/10/16
David
el 9/10/16
Antonius Benedictus
el 9/10/16 -
María José Ledesma
el 9/10/16Hola! No sabría resolver el limite cuando x tiende a -infinito y a infinito de la función:
f(x)= ln (1/x)
¿Alguien sabrá la respuesta?
¡Mil gracias y saludos! :)
Antonio Silvio Palmitano
el 9/10/16Primero, observa que el argumento del logaritmo debe ser estrictamente mayor que cero, por lo que el dominio de la función es el intervalo: D = (0,+inf).
Luego, puedes aplicar la propiedad del logaritmo de un cociente y tienes:
f(x) = ln1 - lnx = 0 - lnx = - lnx.
Luego, revisa tus apuntes de clase y verás que la gráfica de la función lnx tiene asíntota vertical inferior x = 0 (observa que cuando x tiende a 0 por la derecha, la función lnx tiende a - infinito), y observa también que cuando x tiende a +infinito, la función lnx tiende a +infinito.
Por lo tanto, podemos plantear para la función de tu ejercicio:
Lím(x-->+inf) f(x) = Lím(x-->+inf) (- lnx) = - inf.
Lím(x-->0+) f(x) = Lím(x-->0+) (- lnx) = + inf.
Puedes corroborar los resultados mediante un gráfico de la función f(x), que puedes hacer con algún programa informático.
Espero haberte ayudado.
-
emerson acosta
el 9/10/16Me ayudan con este limite por favor? cuando lo hago me da cero (0) pero el resultado es 1/36
Se que me debo estar equivocando al aplicar la conjugada en el numerador. Gracias de ante mano.
Antonio Silvio Palmitano
el 9/10/16Veamos la expresión de la función, es una expresión fraccionaria, cuyo numerador (N) puede escribirse (indicamos raíz cúbica como (3V)):
N = ( (3V)(h) )^2 - 2*(3V)(h) + 1 = ( (3V)(h) - 1)^2.
Luego, tenemos un cuadrado en el numerador (N) y otro cuadrado en el denominador (D), por lo que la expresión fraccionaria puede escribirse:
N/D = ( (3V)(h) - 1)^2 / (h^2 - 1) = asociamos potencias = ( ((3V)(h) - 1) / (h^2 - 1) )^2.
Luego podemos plantear la sustitución (cambio de variable):
t = (3V)(h), de la que tenemos: t^3 = h, y también: t^6 = h^2, y observa que t tiende a 1 cuando h tiende a 1, sustituimos y la expresión fraccionaria queda:
N/D = ( (t - 1) / (t^6 - 1) )^2
Luego, observa que el denominador puede ser factorizado con la regla de Ruffini (raíz: 1) y la expresión queda:
N/D = ( (t - 1) / ( (t -1)*(t^5 + t^4 + t^3 + t^2 + t + 1) ) )^2 = simplificamos = ( 1/(t^5 + t^4 + t^3 + t^2 + t + 1) )^2
Luego, tomas el límite cuando t tiende a 1 y queda:
Lím(t-->1) ( 1/(t^5 + t^4 + t^3 + t^2 + t + 1) )^2 = (1/6)^2 = 1/36.
Espero haberte ayudado.
-
Robert
el 9/10/16Hola gentee de unicoos. Necesito gran ayuda con este ejercicio. De verdad que no lo entiendo. Quiero que me lo expliquen. Gracias.
Antonio Silvio Palmitano
el 9/10/16Te recomiendo recurras a los vìdeos del tema: integrales impropias.
Va una orientaciòn:
1º) Plantea la integral indefinida, por ejemplo para tu primer ejercicio queda: -2*x^(-1/2) + C = -2/V(x) + C.
2º) Luego resuelve la integral definida, reemplazando el lìmite impropio (+infinito) por una indeterminada b, lo haces y queda: - 2/V(b) + 2.
3ª) Planteas el lìmite para b tendiendo a +infinito de la expresión anterior (observa que el primer tèrmino tiende a cero), lo haces y llegas a: I = 2.
Por lo tanto, la integral del primer ejercicio es convergente (y si te hubiese quedado infinito en el resultado, serìa divergente).
Haz el intento con el siguiente ejercicio.
Espero haberte ayudado.
-
PauArias_11
el 9/10/16Hola! Hay algún vídeo relacionado con factoriales y números combinatorios?
Muchas graciass
Francisco Javier Cardama
el 9/10/16Aquí te paso los 5 vídeos que tiene unicoos sobre combinatoria, un saludo y mucha suerte :-)
http://www.unicoos.com/video/matematicas/4-eso/combinatoria/permutaciones/combinatoria-02-permutaciones-sin-repeticion
-
María
el 9/10/16Hola, ¿alguien me podría ayudar con este ejercicio de matrices? No lo entiendo, lo único que he pensado es igualar la matriz A y B a 0 para poder calcular λ.
Antonio Silvio Palmitano
el 9/10/16
