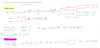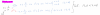-


Antonio Silvio Palmitano
el 10/10/16Has planteado bien las fracciones parciales, y has obtenido una igualdad entre los numeradores. Observa que tienes planteada correctamente una igualdad entre polinomios, por lo que debe cumplirse para cualquier valor de x.
Para x = 1/2 queda: 1/2 = 3B, de donde despejas: 1/6 = B.
Para x = -1/4 queda: -1/4 = (-3/2)A, de donde despejas: 1/6 = A.
Luego la integral queda para resolver como una suma de integrales:
I = I1 + I2, en la que enemos:
I1 = (1/6)*Integral (1/(4x+1))*dx (puedes resolverla con la sustitución: t = 4x+1).
I2 = (1/6)*Integral (1/(2x-1))*dx (puedes resolverla con la sustitución: w =2x-1).
Espero haberte ayudado.
-
Buenas unicoos podrian ayudarme en este ejercicicio: no encuentro como resolverlo. La respuesta correcta es la opcion: d)



Antonio Silvio Palmitano
el 10/10/16Recuerda las expresiones del seno de la suma y de la resta de dos ángulos:
sen(a+b) = sena*cosb+cosa*senb
sen(a-b) = sena*cosb-cosa*senb
Luego veamos el numerador (N):
N = sen(a+b)+sen(a-b) = sena*cosb+cosa*senb + sena*cosb-cosa*senb = cancelamos términos opuestos y reducimos términos semejantes = = 2*sena*cosb.
Luego veamos el denominador (D):
D = sen(a+b)-sen(a-b) = sena*cosb+cosa*senb - (sena*cosb-cosa*senb) = distribuimos el agrupamiento:
= sena*cosb+cosa*senb - sena*cosb+cosa*senb = cancelamos términos opuestos y reducimos términos semejantes = 2*cosa*senb.
Luego, la expresión queda:
N/D = 2*sena*cosb / (2*cosa*senb) = simplificamos factores numéricos = sena*cosb / cosa*senb = escribimos como producto de expresiones fraccionarias:
= (sena/cosa)*(cosb/senb) = aplicamos las identidades trigonométricas de la tangente y la cotangente = tana * cotgb.
Espero haberte ayudado.
-
Hola Uniccos, me pueden ayudar con este problema de ECUACIONES DIFERENCIALES DE PRIMER ORDEN por favor.



Antonio Silvio Palmitano
el 10/10/16Vamos con una orientación.
Puedes plantear la sustitución (cambio de variable): w = ax+by+c, en la que derivas con respecto a x queda: w' = a+by', y luego despejas: (w'-a)/b = y'.
Luego sustituyes y la ecuación queda:
(w'-a)/b = (tanw)^2, haces pasaje de divisor como factor, luego pasaje de término y queda:
w' = b*(tanw)^2 + a (*).
Luego, puedes plantear una nueva sustitución: z = tanw, en la que al derivar con respecto a x queda:
z' = (secw)^2 * w' = ((tanw)^2 + 1)*w', luego sustituyes nuevamente y queda: z' = (z^2 + 1)*w', luego despejas y llegas a: z' / (z^2 + 1) = w'.
Luego sustituyes en la ecuación señalada (*) y queda:
z' / (z^2 + 1) = bz^2 + a, haces pasaje de divisor como factor, escribes a la derivada de z como cociente entre diferenciales y queda:
dz/dx = (z^2 + 1)(bz^2 + a), haces pasajes de divisor como factor y de factores como divisores para separar variables y queda:
( 1 / (z^2 + 1)(bz^2 + a) )*dz = dx.
Luego, observa que a la izquierda puedes proseguir con el método de las fracciones parciales.
Espero haberte ayudado.
-
Hola buenas tardes tengo problemas con una tarea y quiero solicitar su ayuda Tengo que hacer la siguiente función
f(x)= [x] + [-x]
Que me imagino es parte entera de x y -x Donde tengo que demostrar que el Límite cuando x tiende a 2 existe, pero f(2) la imagen de 2 no es igual al límite -
Hola, soy pésima con las demostraciones, me podrían ayudar a resolver esto de una manera sencilla, por favor?



Antonio Silvio Palmitano
el 10/10/16Indicamos z conjugado como z'.
Probaremos por inducción completa (h pertenece a N):
P(1): (z^1)' = aplicamos la primera definición = z', es Verdadera.
P(h): (z^h)' = (z')^h, aceptamos que es Verdadera (Hipótesis Inductiva).
P(h+1): ( z^(h+1) )' = (z')^(h+1), que debemos demostrar (Tesis Inductiva).
Demostración:
( z^(h+1) )' = aplicamos la segunda definición:
= ( z^h * z^1 )' = aplicamos la primera definición:
= ( z^h * z )' = aplicamos propiedad del conjugado de un producto:
= (z^h)' * z' = aplicamos la Hipótesis Inductiva:
= (z')^h * z' = aplicamos la primera definición:
= (z')^h * (z')^1 = aplicamos propiedad del producto de potencias con bases iguales:
= (z')^(h+1).
Luego, por el Principio de Inducción (5° axioma de Peano), tenemos que (z^n)' = (z')^n, para todo n perteneciente a N.
Espero haberte ayudado.
-
He intentado realizar el ejercicio de dos maneras, pero no localizo el error de la segunda opción. ¿Estoy realizando alguna operación incorrecta? Creo que la igualdad la mantengo, ¿No? Gracias


Antonio Silvio Palmitano
el 10/10/16A partir de la inecuación x > 1/x, debes considerar dos opciones: x > 0 y x < 0, desarrollas ambas y obtendrás subintervalos del intervalo solución.
1°) Para x > 0 (*),
hacemos pasaje de divisor como factor (observa que x toma valores positivos, por lo que no se altera la desigualdad) y queda:
x^2 > 1, luego hacemos pasaje de potencia como raíz (recuerda que si la potencia es par debemos consignar el valor absoluto de la base):
|x| > V(1), resolvemos la raíz positiva a la derecha y queda:
|x| > 1, que nos conduce a dos opciones:
a) x < -1 (que contradice la inecuación señalada (*)),
b) x > 1 (**) (que no contradice la inecuación señalada (*)),
por lo tanto, por las inecuaciones señaladas (*) y (**) tenemos el subintervalo (1,+inf) (***).
2°) Para x < 0 (****),
hacemos pasaje de divisor como factor (observa que x toma valores negativos, por lo que si se altera la desigualdad) y queda:
x^2 < 1, luego hacemos pasaje de potencia como raíz (recuerda que si la potencia es par debemos consignar el valor absoluto de la base):
|x| < V(1), resolvemos la raíz positiva a la derecha y queda:
|x| < 1, que nos conduce a:
-1 < x < 1, y teniendo en cuenta la inecuación señalada (****) nos queda el subintervalo: (-1,0) (*****).
Luego, el intervalo solución será la unión de los subintervalos señalados (***) y (*****):
S = (-1,0) u (1,+inf).
Espero haberte ayudado.
-
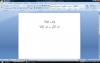
Hola, me gustaría resolver el siguiente problema de matemáticas, para poder explicárselo a mi hijo. "Calcula cuanto debe valer en cada caso x e y para que se verifique la igualdad." Muchísimas gracias. Saludos...


Antonio Silvio Palmitano
el 10/10/16Una forma es buscar el mínimo común múltiplo entre los índices de las raíces, y elevar a cada miembro de la igualdad con un potencia con exponente igual a dicho mínimo común índice.
En el primer ejercicio tienes una raíz quinta (indicamos (5V)) y una raíz con índice 15 (indicamos (15V)), y observa que el mínimo común múltiplo entre 5 y 15 es 15, por lo tanto elevamos ambos miembros a la 15 y queda:
((15V)(2^x))^15 = ( (5V)(2) )^15, luego podemos simplificar potencias y raíces (observa que a la izquierda se cancelan):
2^x = 2^3, luego comparando expresiones tenemos:
x = 3.
En el segundo ejercicio, observa que tienes raíz de índice 12 (indicamos (12V)) y raíz de índice 2 o cuadrada (indicamos V), y el mínimo común múltiplo ente 2 y 12 es 12, por lo tanto elevamos ambos miembros a la 12 y queda:
( (12V)(2^x) * 3^y )^12 = ( V(2^2) * 3^5)^12, luego distribuimos potencias entre los factores en cada miembro:
( (12V)(2^x) )^12 * (3^y)^12 = ( V(2^2) )^12 * (3^5)^12, luego simplificamos raíces y potencias (observa que tenemos cancelación en el primer factor a la izquierda).
2^x * (3^y)^12 = (2^2)^6 * (3^5)^12, resolvemos las potencias cuyas bases son potencias (recuerda que se multiplican los exponentes):
2^x * 3^(12y) = 2^12 * 3^60, luego comparamos factores y tenemos la solución:
x = 12 (comparando las potencias con base 2)
12y = 60 (comparando las potencias con base 3), de donde despejamos y queda: y = 60/12 = 5.
Espero haberte ayudado.
-
Buenas tardes.Necesito ayuda con esta derivada. Tengo la funcion F(x)=-x^2 . e^x (menos equis al cuadrado multiplicado por e elevado a la equis)
Necesito que me muestren como hacer la segunda derivada de eso, llego hasta la primera..pero en la segunda tengo inconvenientes.Gracias de antemano


Antonio Silvio Palmitano
el 9/10/16Observa que tienes un producto de funciones, por lo que la derivada primera queda:
F ' (x) = -2x*e^x - x^2* e^x = extraemos como factor común el factor exponencial = (-x^2 - 2x)*e^x.
Observa que para volver a derivar, tenemos un producto, luego la derivada segunda queda:
F ' ' (x) = (-2x - 2)*e^x + (-x^2 - 2x)*e^x = extraemos como factor común al factor exponencial = (-2x - 2 - x^2 -2x)*e^x = (-x^2 -4x-2)*e^x.
Espero haberte ayudado.
-
BS unicoos, ayudenme en este ejercicio no encuentro como llegar a la solucion del ejercicio que es: tg^3x= 8raiz5/25.




Antonio Silvio Palmitano
el 10/10/16Partimos de la ecuación: (cosecx)^4 = 81/16, luego hacemos pasaje de potencia como raíz (indicamos raíz cuarta como (4V):
cosecx = (4V)(81/16), resolvemos (observa que 81/16 = (3/2)^4):
cosecx = 3/2, luego aplicamos identidad trigonométrica par la cosecante:
1/senx = 3/2, despejamos y queda:
2/3 = senx (*), luego aplicamos identidad trigonométrica para el coseno:
cosx = V(1 - (senx)^2), reemplazamos según la ecuación señalada (*) y queda:
cosx = V(1 - (2/3)^2), resolvemos el argumento de la raíz y queda:
cosx = V(5/9), distribuimos la raíz y resolvemos en el denominador:
cosx = V(5)/3 (**).
Luego, a partir de las ecuaciones señaladas (*) y (**) planteamos identidad trigonométrica para la tangente:
tanx = senx/cosx = reemplazamos = (2/3) / (V(5)/3) = resolvemos = 2/V(5), luego multiplicamos y dividimos por V(5) y queda:
tanx = (2*V(5)) / (V(5))^2 = simplificamos raíz y potencia en el denominador = 2*V(5)/5.
Luego, elevamos al cubo en ambos miembros y queda:
(tanx)^3 = (2*V(5)/5)^3, distribuimos la potencia = 2^3 * (V(5))^3 / 5^3 = resolvemos potencias y queda:
(tanx)^3 = 8*V(5^3)/125, descomponemos el argumento de la raíz en factores con bases iguales:
(tanx)^3 = 8*V( 5 * 5^2 )/125, distribuimos la raíz:
(tanx)^3 = 8*V(5)*V(5^2)/125, simplificamos raíz y potencia:
(tanx)^3 = 8*V(5)*5/125, simplificamos por 5 y llegamos a:
(tanx)^3 = 8*V(5)/25.
Espero haberte ayudado.