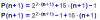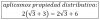-
A ver si alguien puede ayudarme, estoy atascado con el siguiente ejercicio, me piden que demuestre por inducción que la solución de
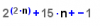 donde n es un numero natural n ≥1 es multiple de 3.
donde n es un numero natural n ≥1 es multiple de 3.veo que se cumple para n = 1:
y al demostrarlo para n+1, veo que 15·(n+1) es multiple de 3, porque esta multiplicando por 15 que ya es multiplo de 3.
Pero no sé razonar por qué 22·(n+1)-1 también lo es y la suma de 2 numeros multiples de 3 es multiple de 3 (veo que el 2 siempre estará elevado a un exponente par, pero no sé si esto es alguna propiedad o si tiene algo que ver).
Espero que alguien pueda ayudarme, saludos!


Antonio Silvio Palmitano
el 7/10/16P(1) se cumple, ya lo has demostrado.
Tesis Inductiva P(h+1): 2^(2(h+1)) + 15(h+1) - 1 = distribuimos en el exponente del primer término:
= 2^(2h+2) + 15(h+1) - 1 = aplicamos propiedad del producto de potencias con bases iguales en el primer término:
= 2^(2h) * 2^2 + 15(h+1) - 1 = resolvemos y operamos en el primer término:
= 4*2^(2h) + 15(h+1) - 1 = sumamos, restamos y agrupamos en el factor que no es numérico en el primer término:
= 4*( (2^(2h) + 15h - 1) - 15h + 1 ) + 15(h+1) - 1 = distribuimos en el primer término:
= 4*(2^(2h) + 15h - 1) - 60h + 4 + 15(h+1) - 1 = reducimos términos semejantes:
= 4*(2^(2h) + 15h - 1) - 60h + 15(h+1) + 3 = extraemos factor común 3 en los tres últimos términos:
= 4*(2^(2h) + 15h - 1) + 3(-20h + 5(h+1) + 1).
Observa que en el primer término tienes el cuádruple de un múltiplo de 3, por Hipótesis Inductiva, y se suma luego con otro múltiplo de 3 (observa que en el agrupamiento tienes suma de números enteros), por lo que hemos demostrado que la tesis inductiva es verdadera.
Espero haberte ayudado

Oscar
el 8/10/16Gracias Antonio y Cesar! He entendido todo el procedimiento menos este paso:
= 4*2^(2h) + 15(h+1) - 1 = sumamos, restamos y agrupamos en el factor que no es numérico en el primer término:
= 4*( (2^(2h) + 15h - 1) - 15h + 1 ) + 15(h+1) - 1 = distribuimos en el primer término:
De donde sale el "+ 15h - 1) - 15h + 1" ?Se le aplica alguna propiedad? Aparece a causa de la separación de los exponentes con la misma base?
Con el desarrollo de César tampoco he podido entenderlo.
-
No se me ocurre como hacer este ejercicio, hice el triangulo y todo... pero solo tengo un angulo y un lado al final, no se si lo estare haciendio mal o algo... pero no se como aplicar el teorema del coseno en esto :C! Help


Antonio Silvio Palmitano
el 7/10/16Observa (seguramente ya has hecho un dibujo) que los vértices del triángulo coinciden con la posición de los conos, y observa también que los ángulos en el segundo y en el tercer vértice (cono) son los ángulos exteriores, por lo que conoces dos ángulos interiores:
en el segundo cono: A = 180° - 100° = 80°
en el tercer cono: B = 180° - 130° = 50°
y luego puedes calcular el ángulo interior correspondiente al primer cono: C = 180° - (80° + 50°) = 180° - 130° = 50°.
Observa que tienes información sobre el lado con extremos en el primero y en el segundo cono, en cuyo vértice opuesto está ubicado el tercer cono (ángulo B = 50°), y la longitud del lado puede planteare:
a = v*5 = 5v.
Luego, el lado que une al tercer cono con el primero tiene longitud: v*t, y su ángulo opuesto está ubicado en el segundo cono (A = 80°).
Luego planteamos el Teorema del seno:
sen50° / (5v) = sen80° / vt, haces pasajes de divisor como factor y de factor como divisor y queda:
vt / (5v = sen80° / sen50°, simplificas a la izquierda y haces pasaje de divisor como factor y queda:
t = 5*sen80° / sen50°,
y la longitud del tramo entre el tercero y el primer cono queda: L(3-1) = v * 5*sen80° / sen50°.
Queda para que plantees las longitud del tramo restante también con el mismo teorema que hemos aplicado.
Espero haberte ayudado.
-
Dado el sistema :
ax-y+az=0
3x+2y+z=2
ax-y-az=0
cuales son los valores de a para ser un sistema compatible determinado, compatible indeterminado o incompatible


Antonio Silvio Palmitano
el 7/10/16Observa que es un sistema de tres ecuaciones con tres incógnitas, por lo que podemos plantear el determinante dela matriz A, cuyos elementos son los coeficientes de las incógnita:
det(A) =
| a -1 a |
| 3 2 1 | = desarrollamos =
| a -1-a |
= a(-2a+1) -(-1)(-3a-a) + a(-3-2a) = distribuimos:
= -2a^2 + a - 3a - a - 3a - 2a^2 = reducimos términos semejantes:
= -4a^2 - 6a =
= -2a(2a + 3).
Luego, observa que el determinante se anula para los valores a1 = 0 y a2 = -3/2, por lo que tenemos tres casos:
A) Si a es distinto de 0 y distinto de -3/2 entonces el sistema es compatible determinado y tiene solución única.
Para los demás casos, reemplazamos los valores y resolvemos el sistema:
B) Si a = 0 tenemos el sistema:
- y = 0, de donde tenemos: y = 0 (*)
3x + 2y + z = 2
- y = 0
Luego reemplazamos el valor señalado (*) en la segunda y en la tercera ecuación y queda el sistema:
3x + z = 2, de donde podemos despejar: z = -3x + 2
0 = 0, que es una identidad verdadera.
Por lo tanto, tenemos que el sistema de tres ecuaciones con tres incógnitas es compatible indeterminado y admite infinitas soluciones, expresadas:
x perteneciente a R
y = 0
z = -3x + 2
y su conjunto solución queda: S = { (x , 0 , -3x + 2), x perteneciente a R }.
C) Si a = -3/2 tenemos el sistema:
(-3/2)x - y + (-3/2)z = 0
3x + 2y + z = 2
(-3/2)x - y - (-3/2)z = 0
Multiplicamos por -2 en todos los términos de la primera y de la tercera ecuacón y el sistema queda:
3x + 2y + 2z = 0
3x + 2y + z = 2,
3x + 2y - z = 0, de donde podemos despejar: 3x + 2y = z (**)
Luego, sustituimos la expresión de z señalada (**) en las dos primeras ecuaciones, y nos queda el sistema de dos ecuaciones con dos incógnitas:
3x + 2y + 2(3x + 2y) = 0, distribuimos y reducimos términos semejantes y queda: 9x + 6y = 0
3x + 2y + 3x + 2y = 2, reducimos términos semejantes y queda: 6x + 4y = 2
Por lo tanto, tenemos el sistema:
9x + 6y = 0
6x + 4y = 2
Multiplicamos por 1/# en todos los términos de la primera ecuación, y por 1/2 en todos los términos de la segunda y el sistema queda:
3x + 2y = 0, de donde despejamos: y = (-3/2)x (***)
3x + 2y = 1
Luego sustituimos la expresión de y señalada (***) en la segunda ecuación y queda:
3x + 2(-3/2)x = 1, resolvemos a la izquierda y queda:
0 = 1,
que es una identidad absurda, por lo que concluimos que el sistema de tres ecuaciones es incompatible y no tiene solución.
Espero haberte ayudado.
-
x+2y=1
2x+(m-1)y=4
cual es el valor de m para que sea un sistema incompatible ?


Antonio Silvio Palmitano
el 7/10/16Puedes despejar x en la primera ecuación y queda: x = -2y + 1, luego sustituyes en la segunda ecuación y queda:
2(-2y + 1) + (m - 1)y = 4, distribuyes y queda:
- 4y + 2 + my - y = 4, haces pasaje de término, reduces términos semejantes y queda:
- 5y + my = 2, extraes factor común a la izquierda y queda:
(-5 + m)y = 2.
Luego, observa que si - 5 + m = 0, de donde despejas: m =5, la ecuación queda:
0y = 2, que te conduce a la identidad:
0 = 2, que es absurda, y el sistema resulta ser incompatible.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/10/16Vamos con una orientación.
Primero tienes que tener a la vista el enunciado del Teorema.
Luego, observa que debes verificar que la ecuación diferencial (que es de orden 1 y de grado 1) tiene la forma:
y ' = f(x,y)
y en tu ejercicio tienes: f(x,y) = V(1 - x^2 - y^2) = ( 1 - x^2 - y^2 )^(1/2),
y puedes verificar que su dominio es: D = { x^2 + y^2 <= 1 }, cuyo gráfico es un disco circular cerrado con centro C(0,0) y radio R = 1, y que la función f es continua en D
Luego, por hipótesis del teorema, derivamos parcialmente a f con respecto a y:
df/dy = - y / V(1 - x^2 - y^2) = -y*(1 - x^2 - y^2)^(-1/2),
y puedes verificar que su dominio es E = { x^2 + y^2 < 1 }, cuyo gráfico es un disco circular abierto, con centro C(0,0) y radio R = 1, y que la función df/dy es continua en E (observa también que E está incluido en D).
Por lo tanto, concluimos que existe un intervalo centrado en xo, tal que la ecuación diferencial tiene solución única, con la condición inicial (xo,yo), en la que el punto (xo,yo) pertenece a E.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 6/10/16Puedes plantear:
tan60° = (x + y)/2
cos60° = 2/(2y)
reemplazas valores y las ecuacones quedan:
V(3) = (x + y)/2
1/2 = 2/(2y)
luego, en la segunda ecuaciópn haces pasajes de divisores como factores, resuelves y queda:
2y = 4, de donde despejas: y = 2.
Luego reemplazas en la primera ecuación y queda:
V(3) = (x + 2)/2, haces pasaje de divisor como factor y queda:
2V(3) = x + 2, hacemos pasaje de término y queda:
2V(3) - 2 = x.
Luego, sumamos las longitudes de los lados del triángulo para calcular su perímetro:
El cateto adyacente al ángulo de 60° tiene longitud 2,
el cateto opuesto al ángulo de 60° tiene longitud: x + y = 2V(3) -2 + 2 = 2V(3),
la hipotenusa tiene longitud: 2y = 2*2 = 4.
Por lo tanto calculamos su perímetro y qeuda:
Per = 2 + 2V(3) + 4 = 6 + 2V(3).
Espero haberte ayudado.