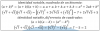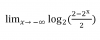-
Miriam
el 5/10/16 -
Jacqueline Peralta
el 5/10/16DERIVADAS
en este video de Unicoos: https://www.youtube.com/watch?v=pz8yjIEL6jg
Profe ayudeme por favor ! No entiendo por que en algunos videos se hace de una frma y en este de otra. Mi duda es esta: deciamos que cuando hay "algo/lo que sea" elevado a un n°, hacemos n°.(lo que sea) elevado a n-1 . (lo que sea)´ Pero cuando es (x) elevado a n° lo que hacemos es n°(x) elevado a n-1 Mi pregunta es, acaso lo que esta dentro del parentesis del primer ejercicio no es un "lo que sea" y por lo tanto deberiamos multiplicar por la derivada del "lo que sea" ?? Por que se lo toma como que es solo X elevado a un N° y se hace solo n(x) elevado a n-1 ???? Ayudaaaaa rindo mañana !!!!!!!!!
Fran
el 5/10/16Cuando tenemos una funcion elevada a un numero, por ejemplo (2x2+3x+4)2 la derivada de esto es 2(2x2+3x+4)1* (4x+3), utilizando la regla de la cadena; sin embargo si tenemos (x)2 la derivada de esto seria 2(x)1 por la derivada de la funcion dentro del parentesis que en este caso la derivada de x es 1.
-
Marmeladeprincess
el 5/10/16Buenas tardes, llevo como 1 hora y media intentando preguntar en foros esta resta de radicales en forma de ración y creo que este sitio me puede ayudar.
Me da 1/2 pero la solución correcta es otra. Gracias por vuestra atención y espero recibir algún comentario.
Marmeladeprincess
el 5/10/16Marmeladeprincess
el 5/10/16 -
Miriam
el 5/10/16Aqui dejo un problema, alguien sabe resolverlo?
Se considera una circunferencia K y 200 puntos distintos sobre K. Cada punto esta en el extremo de un diametro correspondiente a una cantidad entera de grados. Justifica que al menos hay dos puntos que son extremos distintos del mismo diametro.
Gracias.
-
Judith
el 5/10/16Hola! No encuentro el fallo, con lo que no se cual esta bien..😠 Agradecería si me dijerais cual esta bien el fallo q tengo... ¿(Folio/Cuaderno)?
-
Celia Garrido
el 5/10/16Buenas tardes!
¿Me podrían ayudar con este límite?
¡Muchas gracias!
Celia.
Antonio Silvio Palmitano
el 5/10/16Observa que el límite para x tendiendo a - infinito de 2^x es igual a cero.
Obsrva que el argumento del logaritmo en base 2 puede escribirse: 2/2 - 2^x / 2 = 1 - (1/2)*2^x.
Luego, como logaritmo en base dos es una función continua, tenemos (escribimos LOG):
Lím(x-->-inf) LOG( 1 - (1/2)*2^x ) = LOG( Lím(x-->-inf) ( 1 - (1/2)*2^x ) = LOG( 1 - (1/2)*0 ) = LOG(1) = 0.
Espero haberte ayudado.
-
Víctor Miranda
el 5/10/16
Por favor a ver si alguien consigue ayudarme con este ejercicio
David
el 6/10/16Dado que la tabla muestra la longitud del muelle (no lo que se ha alargado) y que la funcion es Peso=k.x, siendo x el alargamiento, deberás hacer una nueva tabla con los pesos y el alargamiento x, que será 0m para un peso de 0N, 0,04 m para un peso de 0,1 N, 0,05m para un peso de 0,2 N, etc, etc, etc
Te sugiero además que representes los puntos en una grafica (en el eje x el alargamiento, en el eje y el peso).. Si todos ellos conforman una recta perfecta, solo tendrás que obtener la pendiente de esa recta, que te indicará la constante elastica del muelle k... Funcion afin 01 (y=mx+n) si no forman una recta te vendría genial este otro... Interpolacion y extrapolacion linealUna vez que tengás la funcion Peso = k. alargamiento... solo tendrás que sustituir x por 0,45N o por 2N para obtener el alargamiento...
FISICA Ley de HOOKE
En el apartado c), sustituye x por 0,5 metros y obtendrás el peso...
Te sugiero este vídeo, por supuesto, -
Patricio Morales
el 5/10/16 -
Alex Domínguez
el 5/10/16Me ayudan ?
Si el sistema AX=B tiene solución única, para A∈Mn×n(R) y B∈Mn×1(R), B distinto del vector nulo, entonces:
Seleccione una:a. El vector columna de B no es combinación lineal de los de A. b. A−1B es la solución del sistema.c. AX=0 tiene infinitas soluciones
Gracias !! -
Carla
el 5/10/16
