-
2logx - log (x+6 ) = 2 log2 me da : log x^2 * ((x+6)/2)^-2 = 0 que hice mal ¿?


Antonio Silvio Palmitano
el 26/8/16Observa que puedes aplicar propiedades de los logaritmos en forma más conveniente:
log(x^2) - log(x+6) = log(2^2)
luego:
log( x^2 / (x+6) ) = log(4)
observa que el argumento del logaritmo en el primer miembro obliga que x+6>0, o sea x > -6)
luego compones con la función exponencial inversa en ambos miembros y queda:
x^2 / (x+6) = 4
haces pasaje de divisor como factor y queda:
x^2 = 4(x+6)
luego distribuyes en el segundo miembro, haces pasajes de términos y queda:
x^2 - 4x - 24 = 0
que es una ecuación polinómica cuadrática, luego aplicas la fórmula resolvente y llegas a:
x1 = 2 - V(28) > -6
x2 = 2 + V10 > -6
por lo que las dos soluciones halladas son válidas.
Espero haberte ayudado. -
Estoy resolviendo la integral que hace unos minutos pregunte , y me dijeron que tenía que hacer la división entre polinomios :
(6x^2-1)/(8x^2+2)
Y creo que la estoy haciendo mal
No ? -
Resolverlo que indica? Encontrar los lados y ángulos restantes supongo no?
Se debe suponer también que es un rectángulo no? Y así sabremos un ángulo más(90) y sacar por resta el restante
Si no se realiza así necesito que se me proporcione los datos para sacarlo por favor
Gracias

Antonius Benedictus
el 26/8/16En efecto: calcular lados y ángulos.
No puedes presuponer que el triángulo es rectángulo.
Te dan dos lados y un el ángulo que forman entre ellos.
usa el teorema del Coseno para calcular el tercer lado.
Para uno del los ángulos que faltan, usa con tino el teorema del seno.
Finalmente, resta de 180º la suma de los dos ángulos que tienes. -
Holaaaa únicoos perdón por hacer tantas preguntas. Estoy muy frustrada con esta integral sería de mucha ayuda si me dicen que tengo que hacer despues de donde he quedado .
Gracias ! -
Hola me ayudan con el ejercicio k. Nose como seguir ka resollucion. Tengo que demostrar como llegar a esa desigualdad.
Gracias

Antonio Silvio Palmitano
el 26/8/16Vamos a partir de la desigualdad que debemos demostrar (observa que escribimos al número complejo z en forma cartesiana binómica: z = x + yi, con x e y números reales, y tenemos que Re(z) = x, Im(z) = y, |z| = V(x^2 + y^2)):
|z|*V(2) >= |x| + |y| (observa que todos los términos de la desigualdad son positivos)
Vamos a demostrar la desigualdad, pero con los dos miembros elevados al cuadrado:
( |z|*V(2) ) ^2 >= ( |x| + |y| )^2
Partimos con el primer miembro, e intentaremos llegar al segundo, con una cadena de igualdades y desigualdades:
( |z|*V(2) )^2 = |z|^2 * 2 = |z|^2 + |z|^2 = (x^2 + y^2) + (x^2 + y^2) =
aquí recordemos propiedades de valor absoluto y de cuadrados: x^2 = |x|^2 e y^2 = |y|^2, reemplazamos y queda:
= (|x|^2 + |y|^2) + (|x|^2 + |y|^2) =
a continuación sumamos (en el primer grupo), y restamos (en el segundo grupo) 2*|x|*|y| (observa que no se altera la igualdad) y queda:
= (|x|^2 + 2*|x|*|y| + |y|^2) + (|x|^2 - 2*|x|*|y| + |y|^2) =
observa que nos quedaron dos desarrollos de binomios elevados al cuadrado, factorizamos y queda:
= ( |x| + |y| )^2 + ( |x| - |y| )^2 >=
observa que introducimos una desigualdad, porque vamos a restar el segundo término que es positivo, lo hacemos y queda:
>= ( |x| + |y| )^2 + ( |x| - |y| )^2 - ( |x| - |y| )^2 =
cancelamos los dos últimos términos que son opuestos y llegamos a:
= ( |x| + |y| )^2.
Para concluir, observa que hemos partido con el primer miembro de la desigualdad y, mediante una cadena de igualdades y desigualdades del tipo >= hemos llegado al segundo miembro, por lo que en resumidas cuentas hemos demostrado que:
( |z|*V(2) )^2 >= ( |x| + |y| )^2
por último, extraemos raíz cuadrada positiva en ambos miembros y tenemos finalmente:
|z|*V(2) >= |x| + |y|
que era lo que teníamos que demostrar
Corresponde aquí aclarar que mis Colegas César y Antonio han mostrado el camino, y que nosotros hemos detallado, a fin de colaborar por si debes exponer este ejercicio en clase, o explicárselo a algún compañero de curso.
Espero haberte ayudado.
-
Una pregunta cuando me dicen "sube la integral " a que se refiere y como lo hago ??


Francisco Gutiérrez Mora
el 26/8/16Se refiere a que la pongas en la pregunta que haces. Es fácil, haces clic en la cámara que aparece en la parte inferior derecha de la pregunta que estás escribiendo, seleccionas el archivo, que no puede ser un pdf, y ya está. tambien puedes copiar el archivo de foto y darle a pegar en la pregunta. Un Saludo.
-
Hola unicoos tengo una pregunta bien cortita sobre ecuaciones diferenciales, tengo este ejercicio que dice dy/dx+e^xy=e^x , bueno, el ejercicio me sale si hago por el metodo de factor de integracion, la cual me sale y=1 el resultado, pero he tratado de hacer por el metodo de variables separables haciendo factor comun la e^x, pero es imposible hallar el resultado.
Por qué no me sale el resultado por éste método amigos o quizás no lo estoy haciendo de la forma correcta
Un abrazo





_Thumb.jpg)




_Thumb.jpg)



_Thumb.png)

_Thumb.jpg)





_Thumb.jpg)
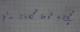

_Thumb.jpg)


