-
marco
el 15/6/16los flags son buenos o malos? siento la impertinencia
Patri
el 15/6/16Hola Marco,
Depende desde donde lo mires, si la pones tú es que has encontrado un error, un fallo, que se sale de los contenidos de unicoos o no se entiende. Si te la aceptan, ganas un flagpoint y al cabo de un par recibes medallas por ello.
Si eres tú el que la recibe es que tu pregunta no se entiende o le falta algo (todas las opciones que se pueden elegir al ponerlo).
Sirven para "vigilar" los foros. -
Andrea
el 15/6/16 -
Pablo
el 15/6/16Problema de Algebra - Calculo de una Base de Subespacio
Hola
Tengo un problema con este ejercicio. Me pide que halle una base para S y otra para T. Para S no tengo ningun problema ya que busco combinaciones lineales y encuentro el valor que "sobra" por asi decirlo.
En el otro caso, en T, me dan una especie de ecuacion y nose que hacer para averiguar las bases.
Muchas gracias
En el otro caso, en T, me dan una especie de ecuacion y nose que hacer para averiguar las bases.
Muchas gracias
">_Thumb.png)
-
Claudialez
el 15/6/16 -
Santafe
el 15/6/16buenas, he estado mirando el vídeo de combinatoria de variaciones sin repetición (https://www.youtube.com/watch?v=h0FwTGtM7H8#t=252.410987), y me ha surgido una duda, no habría que multiplicar el resultado final por 3? Ya que dentro de los 1320 formas que pueden ser elegidos los equipos, cada uno puede tener una función, me explico
No es lo mismo que la persona A sea secretario que que sea vicepresidente.
No sé si estoy en lo cierto o si me expreso bien, un saludo¡ -
Matías
el 15/6/16Buenas tardes, me podrían ayudar con la siguiente integral : ∫ entre 0 y 1 L(1+√u)du. Se debe realizar con cambio de variable ( de derecha a izquierda ) e integración por partes
-
Usuario eliminado
el 15/6/16Hola ¿me podeis hacer esta integral? gracias de todos los colores
Antonio
el 15/6/16Antonio
el 15/6/16 -
Pablo
el 15/6/16Problema de Algebra - Calculo de una Base de Subespacio
Hola
Tengo un problema con este ejercicio. Me pide que halle una base para S y otra para T. Para S no tengo ningun problema ya que busco combinaciones lineales y encuentro el valor que "sobra" por asi decirlo.
En el otro caso, en T, me dan una especie de ecuacion y nose que hacer para averiguar las bases.
Muchas graciasEn el otro caso, en T, me dan una especie de ecuacion y nose que hacer para averiguar las bases.
Muchas gracias">
Marcos
el 15/6/16Saludos,
Lo que te dan es una ecuación, eso significa que, en R^4, necesitas 3 vectores linealmente independientes, que cumplan la ecuación, por ejemplo, los vectores:
v1=(1/2, -1,0,0), v2=(1,0,1,0), v3=(1/3,0,0,-1) son base ya que anulan la ecuación y son linealmente independientes.
Para este tipo de problemas donde tienes una ecuación o varias, lo que va bien, es fijar una variable, y anular las demás excepto una, para ir encontrando de manera rápida las soluciones.
Pablo
el 15/6/16Hola
Estuve viendo lo que me comentas. Lo que hice es lo siguiente
U: x + 2y - z + 3w=0
Despeje X
X= -2y + z -3w
Luego Puse Asi (-2y + z -3w, y,z,w)=0 Osea puse lo que despeje en el lugar de Las X
Luego Acomodode todo de manera que me queden 3 vectores
(-2y,y,0,0) + (z,0,z,0) + (-3w,0,0,w)
Luego
y(-2,1,0,0) + z(1,0,1,0) + w( -3,0,0,1)
Tengo mis dudas ya que a vos te dio distinto, me podrias decir como llegaste a ese resultado o si esta bien lo que acabo de hacer?
Marcos
el 15/6/16Vale, me acabo de dar cuenta que tengo un fallo, pero la solución que has puesto es correcta, es el método adecuado para resolver estas cosas, pero el método que has utilizado solo sirve para una ecuación, o varias si éstas están bien condicionadas. Los vectores que me habían salido están multiplicados por una constante, que a la hora de formar base no importa ya que multiplicar un vector por un escalar no cambia su linealidad:
y(-2,1,0,0) + z(1,0,1,0) + w( -3,0,0,1)
y
y(-4,2,0,0) + z(1/2,0,1/2,0) + w( -3/5,0,0,1/5) son ambas bases del subespacio de la ecuación. E incluso puedes sumar los vectores entre ellos, siempre que sean linealmente independientes. -
Minerva Rabadan
el 15/6/16Halla el valor de k para que los vectores (1,2) y (k, raíz de 3 + 1/2) formen un ángulo de 30 grados
-
Javier Cutillas Zarate
el 15/6/16Buenas, ¿Podriais hacer esta opcion de Pau 2016 matematicas II region de murcia? No estoy conforme con el 6 que me han puesto y quería saber si he cometido tantos errores... Muchas gracias:)
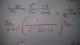
_Thumb.jpeg)
.jpg)
.jpg)
.jpeg)
.jpg)
.jpg)
.png){kind=link}
