-
Hola me podrian ayudar con este ejercicio es que no lo entiendo porque me da el conjunto A={ a,b,c,d} y me pido encontrar el identidad pero, no se si es 1 ya que uno no se encuentra dentro de ese conjunto me podria ayudar porfa
-
hola unicos me pueden ayudar a sacar los valores de y' para poder graficar la siguiente ecuacion diferencial .
y'=x+y
donde al resolverle es igual, donde y es una constantes
y=x^{2}/2 + yx + c.
solo quiero saber como encontrar los valores:
x+y|y'
para poder graficar -
hola buenas noches necesito saber desde 0 vectores rectas y planos con que videos me conviene empezar? gracias!


Adrián
el 21/4/16Rectas y Planos . Aunque siempre puedes empezar desde cursos inferiores para repasar conceptos básicos.
-
Hola unicoos, para hallar la curvatura de la función debo igualar la segunda derivada a 0 y así encontrar los intervalos,pero si no tiene solución al igualar a cero que hago? La función es f(x)=x^2/(2-x)


Antonius Benedictus
el 21/4/16No hay punto de inflexión. sin embargo, puede haber cambio de curvatura. De hecho, después de simplificar, en la derivada segunda te ha de quedar (2-x)^3 en el denominador. Esta expresión es positiva si x<2 y es negativa si x>2. Con esto y con el signo del numerador ya puedes discernir en que semirrecta es cóncava la función y en cuál convexa.
-
Hola muy buenas noches. El problema que les adjunto me tiene un poco perdido. Es el siguiente.
Sean A y B las dos rectas de R3 tales que:
A: α: x+y+z=1 y B: x= 3t + a
β: x-y+2z=3 y= -t + b
z= ct + d
Me piden que calcule C para que A y B sean paralelas. Yo se que serán paralelas si solo si el rango de la matriz de coeficientes es 1 y el rango de la matriz ampliada es 2.
Lo he estado intentando y tengo alguna duda, ya que cuando calculo el rango de la matriz de coeficientes, con el primer menor de orden dos que me encuentro ya es distinto de 0 y no depende de C.
Les adjunto lo que yo he hecho. -
-

César
el 21/4/16Ecuacion de la recta en R²
Ecuacion de la recta en R²
mirate los videos y nos cuentas







_Thumb.jpg)











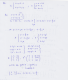

_Thumb.jpg)

_Thumb.jpg)

_Thumb.jpg)


