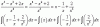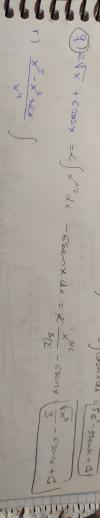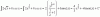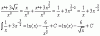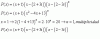Los foros de unicoos se han unificado en beUnicoos. Para dejar preguntas nuevas deberás hacerlo allí, donde además encontrarás el resto de asignaturas y herramientas para ayudarte con tus estudios.
Ir a beUnicoos
Ayuda con el apartado r)? Como continuo por favor
Está bien el apartado q)?
Hola, como hago esta integral por favor:
x⁴+3√x/x²
Buenos dias únicos. Ayer hice una pregunta que me contestó César muy amablemente, pero no me queda nada clara la gráfica con el geogebra. Entiendo perfectamente como hallar el área de la parábola entre esos límites, pero con la recta no sé cómo hacerlo porque si es menor que 1 también podría tomar valores negativos de x ¿no?. Me podéis dar una orientación? Mil gracias 
creo recordar que era entre x=0 y=0 osea primer cuadrante.
Cómo vamos a sacar el punto A? Gracias
multiplico 2+3i por su conjugado luego me queda (x-13) y lo multiplico por (x+1) y llego a x^2-12x-13 pero no me sale encontrar p(1)=20
Si -1 es raiz multiple,puedo realizar la division polinomica larga con x^2+2x+1,pero no estoy seguro si lo tengo bien hecho.
pon lo que has hecho.
A mi me sale que con multiplicidad 3 y a=5 quede bienç
Que tal, tengo este problema sobre encontrar la ecuación del lugar geométrico, lo he estado haciendo mediante el método de distancias entre puntos, pero siempre acabo con el término de equis cuadrada eliminado, así que quisieras preguntarle si estoy fallando en algún paso del procedimiento, de antemano gracias.
quisiera saber si esta bien, los divisores del termino independiente los dividi por el coeficiente principal para hallar las posibles raices
Está bien.
Los factores están bien hallados, pero al final tienes que multiplicar todo por 3.
