-


Antonio Silvio Palmitano
el 21/1/20Observa que tienes que los vectores w y u son ortogonales, entonces tienes que su producto escalar es igual a cero, por lo que puedes plantear la ecuación vectorial:
w • u = 0, sustituyes las expresiones vectoriales, y queda:
< m ; 1 ; n > • < 1 ; 0 ; 1 > = 0, desarrollas el producto escalar, y queda:
m*1 + 1*0 + n*1 = 0, resuelves coeficientes, cancelas el término nulo, y queda:
m + n = 0, de aquí despejas: n = -m (1);
luego, sustituyes la expresión señalada (1) en la ecuación que tienes en tu enunciado, y que corresponde al desarrollo del determinante, y queda:
2(-m) - 2*m - 1 = 0, resuelves el primer término, reduces términos semejantes, y queda:
-4*m - 1 = 0, y de aquí despejas:
m = -1/4;
luego, reemplazas este último valor remarcado en la ecuación señalada (1), resuelves, y queda:
n = 1/4.
Espero haberte ayudado.
-
 4ºESO, problema asociado a un sistema de inecuaciones con dos incógnitas.
4ºESO, problema asociado a un sistema de inecuaciones con dos incógnitas.No entiendo muy bien la lógica del planteamiento del sistema en este problema del que os adjunto la imagen completa del libro. Imagino que se podría deducir (aunque sea en parte) a partir de la pequeña tabla que se incluye en el mismo (tres filas, cuatro columnas). Como podréis ver se trata de una ACTIVIDAD RESUELTA (nº 23), pero aun así no la entiendo. ¿Me podríais ayudar a comprenderlo, por favor? Gracias de antemano.


Jose Ramos
el 21/1/20Se trata de un problema de programación lineal (se estudia en 2º de Bachillerato). Las inecuaciones que conforman el sistema son consecuencia directa de las condiciones que impone el enunciado del problema. El sistema genera una región del plano (en el dibujo zona azul) denominada región factible. Todos los puntos (x,y) de la región factible son las posibles soluciones del problema.


JOSE ANTONIO
el 21/1/20Muchas gracias Jose por tu ayuda y entiendo lo que dices, pero no soy capaz de ver la lógica de la estructura del sistema. El libro que estoy estudiando (obvio la editorial) es de 4º de eso y hay bastantes problemas parecidos a este. Ya sé que una cosa es la resolución del sistema (lo cual, normalmente, no suele ser demasiado difícil) y otra muy distinta, y menos sencilla, generar dicho sistema a partir de un enunciado dado (como es el caso). Si no tienes inconveniente voy a plantear a tu atención, un nuevo problema de características similares a este y enunciado diferente, del que tampoco soy capaz de armar el sistema de inecuaciones. Un saludo.
-


Jose Ramos
el 21/1/20La condición debe verificarse "para todo ∈>0" Para ∈=2, en efecto se cumple porque genera un intervalo centrado en f(2) muy grande, pero si tomamos un valor de ∈ pequeño, por ejemplo ∈=0,1, no encontramos ningún intervalo centrado en 2 de modo que si x está en dicho intervalo, se cumpla que |f(x)-f(2)|<0,1,
-
Buenas.
Tienes un cartón cuadrado. El lado de este cuadrado es de 8dm. Cortas cuatro cuadrados iguales de las esquinas que te permitirán doblar los bordes para hacer una caja. El lado de estos cuadrados es x dm. Exprese el volumen de este cuadro en función de x.
Gracias
-
Buenas. Querría saber la solución de este problema, si puede ser usando Gauss o un sistema de tres ecuaciones sencillo. Muchas gracias.
Los grifos A y B llenan un depósito en 1 h y 10 minutos. Los grifos A y C lo hacen en 1 h y 24 min. Los grifos B y C lo llenan en 2h y 20 min. Determina el tiempo que tarda cada uno por separado y los tres a la vez.











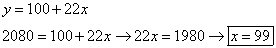 Ya tienes la ecuación
Ya tienes la ecuación















