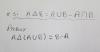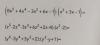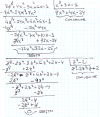-


Breaking Vlad
el 20/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola, necesito ayuda con estos dos ejercicios por favor: (Necesito ver todos los pasos) No hagáis caso a lo que está escrito en azul. Un saludo


David
el 19/1/20Acabo de hacer el primero y sale lo mismo. Lo que Jose ha hecho ha sido: 1º MCD cifras, 2º Parte literal repetida de menor exponente (las letras repetidas al menor exponente, muy importante y fíjate con el ejercicio hecho), 3º sacar fuera del paréntesis lo hecho en 1 y 2 y dentro de él se pone lo que había en cada monomio (identifica lo que es un monomio en tu libro) dividido entre lo que sacaste en 1 y 2. Sabiendo esos tres pasos lo tienes. Practica ejemplos hechos y este otra vez.
-
Tenia una caja de plumas , gaste 2 ⁄ 7 + 4 4 ⁄ 7 , me quedan 2 ⁄ 3, ¿cuantas plumas habian en la caja ?
A mi me salen 95 plumas, pero el resultado del ejercicio da 96, ¿alguien me puede ayudar? con el desarrollo para ver donde esta el fallo,
Gracias de antemano








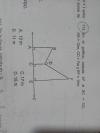


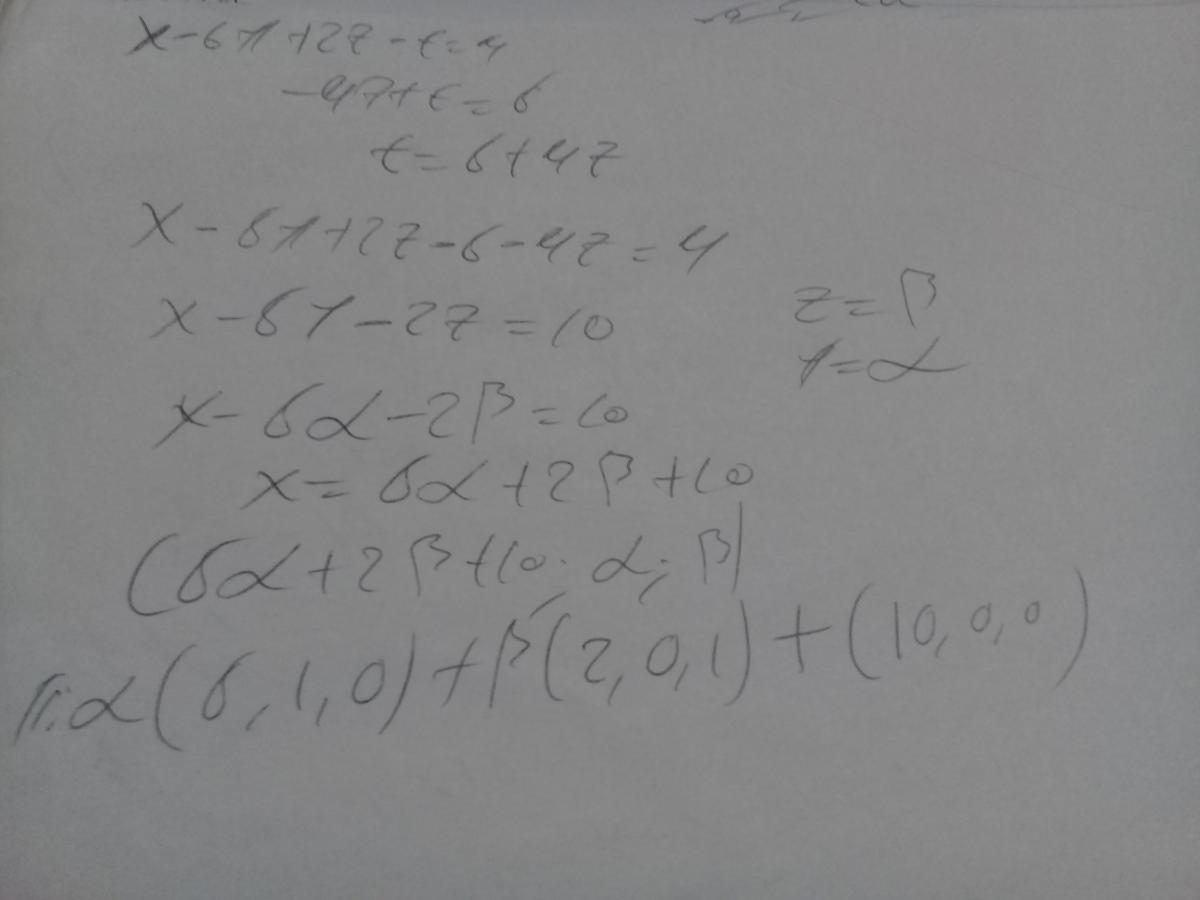
 quisiera saber si esta Bien resuelto?.
quisiera saber si esta Bien resuelto?.