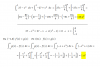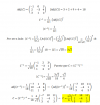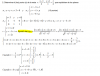-


Antonio Silvio Palmitano
el 18/1/20a)
Observa que 3 es un cero de la función, y observa que 3 pertenece al intervalo de integración: [1;5].
Observa que la función toma valores positivos en el intervalo: [0;3), y que toma valores negativos en el intervalo: (3;5].
Luego, como el cero de la función es punto perteneciente al intervalo, particionas la integral, y la expresión del área queda:
A = |1∫3 (27 - x3)*dx| + |3∫5 (27 - x3)*dx|,
aplicas la definición de valor absoluto en los términos (observa que el argumento del valor absoluto del primer término es positivo, y que el argumento del valor absoluto del segundo término es negativo), y queda:
A = 1∫3 (27 - x3)*dx + ( -3∫5 (27 - x3)*dx ),
resuelves el signo en el segundo término, y queda:
A = 1∫3 (27 - x3)*dx - 3∫5 (27 - x3)*dx,
integras en ambos términos (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
A = [ 27*x - x4/4 ] - [ 27*x - x4/4 ],
evalúas en ambos términos, y queda:
A = ( (27*3 - 34/4) - (27*1 - 14/4) ) - ( (27*5 - 54/4) - (27*3 - 34/4) ), resuelves términos en los agrupamientos primarios, y queda:
A = ( (81 - 81/4) - (27 - 1/4) ) - ( (135 - 625/4) - (81 - 81/4) ), resuelves agrupamientos primarios, y queda:
A = ( 243/4 - 107/4 ) - ( -85/4 - 243/4 ), resuelves en cada término, y queda:
A = 34 - ( -82 ), resuelves, y queda:
A = 116.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 18/1/20b)
Planteas las ecuaciones de las gráficas de las funciones, y queda:
y = 27 - x3,
y = 27 - x,
sustituyes la segunda expresión en el primer miembro de la primera ecuación, y queda:
27 - x = 27 - x3, restas 27 y sumas x3 en ambos miembros, y queda:
x3 - x = 0, factorizas el primer miembro, y queda:
x*(x - 1)*(x + 1) = 0, y por anulación de una multiplicación, tienes tres opciones:
x = 0, que es la abscisa de uno de los puntos de intersección entre las gráficas: A(0,27),
x - 1 = 0, de aquí despejas: x = 1, que es la abscisa de uno de los puntos de intersección entre las gráficas: B(1,26),
x + 1 = 0, de aquí despejas: x = -1, que es la abscisa de uno de los puntos de intersección entre las gráficas: C(-1,28).
Luego, con las abscisas de los tres puntos tienes determinados dos intervalos, para los que elegiremos un valor representativo, y evaluaremos para él las expresiones de las funciones, a fin de determinar cuál de ellas toma valores mayores:
1°)
I1 = (-1;0), representado por: x = -1/2, para quién tienes: f(-1/2) = 217/8 = 27,125, y también tienes: g(-1/2) = 55/2 = 27,5,
por lo que tienes que la función g toma valores mayores que la función f en este intervalo;
luego, planteas la expresión de la porción de área correspondiente a este intervalo, y queda:
A1 = -1∫0( g(x) - f(x) )*dx = -1∫0( (27 - x) - (27 - x3) )*dx = -1∫0( x3 - x )*dx,
aquí integras término a término (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
A1 = [ x4/4 - x2/2 ],
evalúas, y queda:
A1 = ( 04/4 - 02/2 ) - ( (-1)4/4 - (-1)2/2 ),
resuelves términos, y queda:
A1 = 0 - (-1/4),
resuelves, y queda:
A1 = 1/4 (1);
2°)
I2 = (0;1), representado por: x = 1/2, para quién tienes: f(1/2) = 215/8 = 26,875, y también tienes: g(1/2) = 53/2 = 26,5,
por lo que tienes que la función f toma valores mayores que la función g en este intervalo;
luego, planteas la expresión de la porción de área correspondiente a este intervalo, y queda:
A2 = 0∫1( f(x) - g(x) )*dx = 0∫1( (27 - x3) - (27 - x) )*dx = -1∫0( -x3 + x )*dx,
aquí integras término a término (observa que indicamos con corchetes que debes evaluar con Regla de Barrow), y queda:
A2 = [ -x4/4 + x2/2 ],
evalúas, y queda:
A2 = ( -14/4 + 12/2 ) - ( -04/4 + 0/2 ),
resuelves términos, y queda:
A2 = 1/4 - 0,
resuelves, y queda:
A2 = 1/4 (2).
Luego, planteas la expresión del área comprendida entre las gráficas de las funciones f y g como la suma de las áreas que tienes calculadas, y queda:
A = A1 + A2, reemplazas valores, y queda:
A = 1/4 + 1/4, resuelves, y queda:
A = 1/2.
Espero haberte ayudado.
-
 4ºESO sistema de inecuaciones con una incógnita.
4ºESO sistema de inecuaciones con una incógnita.Buenas tardes de nuevo.
Por favor me podéis comentar si la expresión de la solución que he escrito es correcta en el adjunto ejercicio. Me chirría un poco
porque, por una parte, estoy utilizando el símbolo de unión, cuando lo que se sucede en el sistema de inecuaciones son intersecciones. En este caso no existe intersección alguna entre los intervalos dados (ver gráfico). Me pregunto, incluso, si la respuesta a este sistema en concreto sería “no tiene solución”, ya que no existe intersección. No sé si me hago demasiadas preguntas. Gracias por vuestro tiempo y ayuda.


Jose Ramos
el 18/1/20Si es un sistema de inecuaciones, las soluciones son los valores de x que verifican simultáneamente ambas desigualdades. En este caso no los hay, por tanto en este caso, como apuntas, no hay solución, o si quieres es el conjunto vacío: ∅. (Visto de otro modo: la intersección de ambas soluciones parciales es inexistente, no se solapan)
-
Una consulta,siempre se puede calcular la proyeccion ortogonal de Un punto al plano como la interseccion de. La recta al plano,o a veces hay que recurrir a la formula de un vector proyectado a la normal?.


Jose Ramos
el 18/1/20No entiendo bien lo "vector proyectado a la normal".
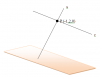
Ahora contesto a la pregunta: Para calcular la proyección ortogonal de un punto sobre un plano, se calcula la intersección de la recta perpendicular al plano (vector director el normal del plano) con dicho plano.
Hay más formas de calcularlo (distancias mínimas) pero se necesitan derivadas parciales y se sale del ámbito del bachillerato.


Antonio Silvio Palmitano
el 18/1/20Si tienes un punto A que es exterior un plano Π, entonces tienes dos maneras para plantear la distancia entre ambos.
1°)
Planteas las ecuaciones cartesianas paramétricas de la recta perpendicular al plano que pasa por el punto A, luego planteas la intersección entre esta recta y el plano para determinar su punto de intersección: B, y luego calculas la distancia entre los puntos A y B, que es igual a la distancia del punto A al plano Π.
2°)
Determinas un punto C perteneciente al plano, luego planteas la expresión del vector AC, y luego calculas el valor absoluto de la proyección del vector AC en la dirección del vector normal al plano, y tienes la distancia del punto A al plano Π.
Espero haberte ayudado.