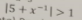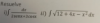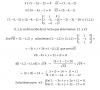-
-


Antonio Silvio Palmitano
el 18/1/20Tienes la inecuación (observa que aplicamos la propiedad de las potencias con exponente negativo en el segundo término del argumento del valor absoluto):
|5 + 1/x| > 1 (*),
y observa que debe cumplirse la condición: x ≠ 0;
luego, extraes denominador común en el argumento del valor absoluto, y queda:
|(5x + 1)/x| > 1, distribuyes el valor absoluto en el primer miembro, y y queda:
|5x + 1|/|x| > 1, multiplicas en ambos miembros por |x| (observa que esta expresión es estrictamente positiva), y queda:
|5x + 1| > |x|, elevas al cuadrado en ambos miembros (observa que los dos miembros son positivos), y queda:
(5x + 1)2 > x2, desarrollas el primer miembro, luego restas x2 en ambos miembros, y queda:
24x2 + 10x + 1 > 0,
factorizas el trinomio cuadrado perfecto en el primer miembro (observa que su coeficiente principal es 24, y que sus raíces son -1/6 y -1/4), y queda:
24*(x + 1/6)*(x + 1/4) > 0, divides en ambos miembros por 24 (observa que no cambia la desigualdad), y queda:
(x + 1/6)*(x + 1/4) > 0;
luego, tienes dos opciones:
1°)
los dos factores son estrictamente negativos, por lo que tienes:
x + 1/6 < 0, de aquí despejas: x < -1/6,
x + 1/4 < 0, de aquí despejas: x < -1/4,
y observa que los elementos que cumplen con ambas inecuaciones pertenecen al intervalo: I1 = (-∞;-1/4);
2°)
los dos factores son estrictamente positivos, por lo que tienes:
x + 1/6 > 0, de aquí despejas: x > -1/6,
x + 1/4 > 0, de aquí despejas: x > -1/4,
y observa que los elementos que cumplen con ambas inecuaciones pertenecen al intervalo: I2 = (-1/6;+∞);
luego, planteas la expresión del conjunto solución de la inecuación de tu enunciado como la unión de los dos intervalos que tienes determinados, con la condición que tienes remarcada (x ≠ 0), y queda:
S = (-∞;-1/4) ∪ (-1/6;0) ∪ (0;+∞).
Espero haberte ayudado.
-

Antonio
el 18/1/20f(x)=xne-x
f'(x)=e-x(nxn-1-xn)
f'(x)=0 => e-x(nxn-1-xn)=0 => nxn-1-xn=0 => xn-1(n-x)=0 => x1=0 ^x2=n
f''(x)=e-x(n2xn-2-nxn-2-2nxn-1+xn)
f''(0)=0
f''(n)=-nn-1<0 => Máx
te dejo hallar la tercera derivada y sustituir el cero
En x=n la función presenta un Máximo y en x=0 un mínimo si n es par y un punto de inflexión si n es impar
-

 halle la recta como interseccion de dos planos,haciendo el producto vectorial de las dos normales tambien lo realize en otra Hoja con z=landa ,el punto de paso,el vector nulo,al hacer z=λ,obtuve x=λ,y=λ, y z=λ , despues hize el producto vectorial de ambas rectas. Para hallar el vector normal,hasta ahi esta bien?.preciso resolucion,saludos cordiales.
halle la recta como interseccion de dos planos,haciendo el producto vectorial de las dos normales tambien lo realize en otra Hoja con z=landa ,el punto de paso,el vector nulo,al hacer z=λ,obtuve x=λ,y=λ, y z=λ , despues hize el producto vectorial de ambas rectas. Para hallar el vector normal,hasta ahi esta bien?.preciso resolucion,saludos cordiales. -


Antonio Silvio Palmitano
el 17/1/20Te mostramos una forma.
Tienes la ecuación diferencial lineal, de primer grado y de primer orden:
y' = y + 2*t*et/(1 + t2), aquí restas y en ambos miembros, y queda:
y' - y = 2*t*et/(1 + t2) (1),
con la condición inicial:
y(0) = 3.
Luego, vamos por pasos.
1°)
Planteas la condición para el factor integrante, y para ello planteas la ecuación diferencial homogénea asociada a la ecuación señalada (1), y queda:
μ' - μ = 0, sumas y en ambos miembros, y queda:
μ' = μ, expresas al primer miembro como un cociente entre diferenciales, y queda:
dμ/dt = μ, separas variables, y queda:
dμ/μ = dt, integras en ambos miembros, y queda (observa que omitimos la constante de integración):
ln(μ) = t, compones en ambos miembros con la función exponencial natural, y queda:
μ = et, que es la expresión del factor integrante.
2°)
Planteas la expresión factorizada de la solución general, con el factor integrante como uno de sus factores, y queda:
y = Y*μ, sustituyes la expresión del factor integrante que tienes en tu enunciado, y queda:
y = Y*et (2),
derivas miembro a miembro en la ecuación señalada (1) (observa que debes aplicar la Regla de la Multiplicación de Funciones en el segundo miembro), y queda:
y' = Y'*et + Y*et (3);
luego, sustituyes las expresiones señaladas (3) (2) en al ecuación diferencial señalada (1), y queda:
Y'*et + Y*et - Y*et = 2*t*et/(1 + t2),
cancelas términos opuestos en el primer miembro, y queda:
Y'*et = 2*t*et/(1 + t2),
divides por et en ambos miembros, y queda:
Y' = 2*t/(1 + t2),
expresas el primer miembro como cociente entre diferenciales, y queda:
dY/dt = 2*t/(1 + t2),
separas variables, y queda:
dY = [2*t/(1 + t2)]*dt,
integras en ambos miembros, y queda (observa que aquí debes corregir en tu desarrollo):
Y = ln(1 + t2) + C;
luego, sustituyes esta última expresión en el primer factor del segundo miembro de la ecuación señalada (2), y queda:
y = [ln(1 + t2) + C]*et,
que es una expresión explícita de la solución general de la ecuación diferencial de tu enunciado.
3°)
Luego, a partir de la condición inicial de tu enunciado, tienes los valores: t = 0, y = 3, los reemplazas en la expresión de la solución general que tienes remarcada, resuelves, y luego despejas:
C = 3,
que es el valor particular de la constante de integración para la condición inicial de tu enunciado;
luego, reemplazas este último valor en la expresión de la solución general, y queda:
y = [ln(1 + t2) + 3]*et,
que es una expresión explícita de la solución particular de la ecuación diferencial de tu enunciado, con la condición inicial allí indicada.
Espero haberte ayudado.