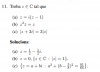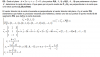-


Antonio Silvio Palmitano
el 13/1/20Vamos con una orientación.
Tienes que la función es derivable en el valor de corte: x = a, por lo que tienes también que es continua en dicho valor; luego, planteas la definición de continuidad de la función en un punto, y queda:
1°)
f(a) = g(a) = 24;
2°)
Lím(x→a-) f(x) = Lím(x→a-) g(x) = g(a),
Lím(x→a+) f(x) = Lím(x→a+) (a*x2 - a2*x + a3) = a3,
y como los límites laterales deben ser iguales para que el límite de la función exista, puedes plantear la ecuación:
g(a) = a3,
y para este valor remarcado tienes: Lím(x→a) f(x) = a3;
3°)
como tienes que el valor de la función f en el punto de corte y el límite de la función f en dicho punto deben ser iguales para que la función sea continua, puedes plantear la ecuación:
a3 = 24, y de aquí despejas: a = ∛(24);
luego, reemplazas este valor en la definición de la función f que tienes en tu enunciado, y queda:
f(x) =
∛(24)*x2 - (∛(24))2*x + (∛(24))3 si x > ∛(24),
g(x) si x ≤ ∛(24),
resuelves coeficientes en la expresión del primer trozo, y queda:
f(x) =
∛(24)*x2 - ∛(576)*x + 24 si x > ∛(24),
g(x) si x ≤ ∛(24).
Luego, planteas la expresión de la función derivada (observa que asumimos que la función g es derivable), y queda:
f'(x) =
2*∛(24)*x - ∛(576) si x > ∛(24),
a determinar si x = ∛(24),
g'(x) si x < ∛(24);
luego, planteas los límites laterales de la función derivada para el valor de corte, y queda:
Lím(x→∛(24)-) f'(x) = Lím(x→∛(24)-) g'(x) = g'[∛(24].
Lím(x→∛(24)+) f'(x) = Lím(x→∛(24)+) [2*∛(24)*x - ∛(576)] = 2*∛(24)*∛(24) - ∛(576) = 2*∛(576) - ∛(576) = ∛(576),
por lo que tienes que la condición que debe cumplirse para que la función derivada esté definida y sea continua en el valor de corte es:
g'[∛(24)] = ∛(576).
Espero haberte ayudado.
-
hola, despues de mas de 15 años quiero retomar mis estudios, voy intentar sacar la ESO en 1 año a distancia, en esos examenes para mayores de 25 años, pero necesito que me digais algún truco de tecnica de estudio. Ya tengo los temarios y solo ver el "tocho" me dan ganas de llorar...
Nunca me gustó estudiar, pero me arrepiento tanto de no hacer las cosas cuando era su momento ... mi cabeza quiere creer que sí puede, pero si lo pienso friamente, algo me dice que va ser dificil hacer los 4 cursos en 1 , bueno en realidad las pruebas libres son en el mes de Mayo, es decir , no tengo ni 5 meses .. necesito algun consejo, trabajo de mañana y de tarde a jornada partida , y mi idea es al salir de trabajar a las 20.00 , ponerme a estudiar de 20:30 a 23:30 todos los días.
Que me podeis decir?
Gracias y espero que me podáis ayudar!


Breaking Vlad
el 13/1/20Hola Nica,
desde unicoos lo que te podemos decir es que nunca es tarde para estudiar, y aunque efectivamente con el tiempo es más difícil, no debes tirar la toalla. Desde nuestros foros nos disponemos a ayudaros con todas las dudas que os surjan durante el estudio.
En cuanto a los consejos, seguramente haya algún unicoo que esté en alguna situación similar o haya pasado por ello y pueda aportate consejos e ideas. Esperemos que se animen.
¡Mucho ánimo y suerte!

Iosef Iglesias
el 2/9/20Hola,
Yo te felicito por la decisión de retomar tus estudios y el esfuerzo que estás haciendo para mejorar tu futuro profesional. Como dice breaking vlad nunca es tarde para estudiar, con determinación y esfuerzo lo puedes conseguir. Yo saqué el bachillerato tarde, no mucho más, pero más tarde de lo normal y me costó muchísimo. Ahora me estoy sacando un curso enfocado al tema del audiovisual para avanzar y encontrar mejor trabajo. Mucha suerte.
-
Alguien me echa una mano con este ejercicio de diferenciabilidad, no lo entiendo muy bien.
Dado un campo escalar tal que f(0,1)=1 y el valor del gradiente (0,1) es (2,1). Definimos F=f(2xy,y). Calcula JF(0,1). Calcula JG(0,1) donde G=f(3x, F(x,y))
Notación: Las mayúsculas son para campos vectoriales y las minusculas para campos escalares. La J indica la matriz jacobiana.
Gracias de antemano


Breaking Vlad
el 15/1/20Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Hola Unicoos!
Tengo una duda con este ejercicio, ya que no consigo entender como se despeja la i para que me de este resultado.
¿Alguien me puede explicar como se despeja la i?
90.000-300 = 30.100 (1+i)-1 + 35.300 (1+i)-2 + 40.500 (1+i)-3
Despejando i= 0,0834341161
Muchas gracias de antemano!