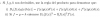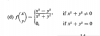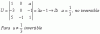-
Hola tengo una duda con un ejercicio espero que me puedan ayudar a resolverlo gracias
Calcula la ecuación general de la recta que pasa por los puntos A(0,-1) y B(3,2).
Gracias

David
el 12/1/20Buenas.
Se empieza sacando el vector director que forman ambos puntos, por ej AB=B-A=(3,2)-=(0,-1)=(3,3)
Después, ponemos la ecuación continua, y tomo el punto A(0,-1):
(x-0)/3=(y-(-1))/3 ; x/3=(y+1)/3
Ahora, lo paso a la ecuación general, que no es más que operar (multiplico en cruz) 3x=3y+3 ; x=y+1 ; x-y-1=0 (ésta es la ecuación general de la recta)
-
Hola!
 Alguien me ayuda a ver el dibujo? No sabría bien donde situar el triángulo. Gracias, mil veces gracias!!
Alguien me ayuda a ver el dibujo? No sabría bien donde situar el triángulo. Gracias, mil veces gracias!!
Antonio
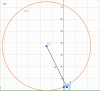
el 12/1/20Debes hallar un punto C que pertenece a la recta r que diste lo mismo al punto A y al punto B,
el triángulo será el formado por los segmentos entre los puntos A y C, los puntos B y C y los puntos A y B,
como la distancia entre los puntos A y C y los puntos B y C es la misma, el triángulo será isósceles.
Sea un punto C de cordenadas C(x,y,z), como pertenece a la recta r debe cumplir su ecuación:
x=1-λ
y= λ
z=3+λ
calculemos ahora la distancia entre A y C: d(A,C)=d((-1,2,0),(x,y,z))=√[(x+1)2+(y-2)2+(z)2]
a continuación calculemos la distancia entre B y C: d(A,C)=d((1,0,-4),(x,y,z))=√[(x-1)2+(y)2+(z+4)2]
igualamos ambas distancias: √[(x+1)2+(y-2)2+(z)2]=√[(x-1)2+(y)2+(z+4)2]
sustituimos: √[(1-λ+1)2+( λ-2)2+(3+λ)2]=√[(1-λ-1)2+( λ)2+(3+λ+4)2]
resolvemos: (1-λ+1)2+( λ-2)2+(3+λ)2=(1-λ-1)2+( λ)2+(3+λ+4)2
(2-λ)2+( λ-2)2+(3+λ)2=(-λ)2+( λ)2+(7+λ)2
4-4λ+λ2+λ2-4λ+4+9+6λ+λ2=λ2+λ2+49+14λ+λ2
4-4λ-4λ+4+9+6λ=+49+14λ
-16λ=32
λ=-2
por lo tanto sustituyendo:
x=1-λ=1-(-2)=3
y= λ=-2
z=3+λ=3+(-2)=1
obtenemos que el punto C es de coordenadas (3,-2,1)
-
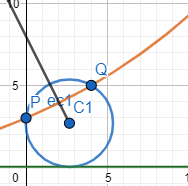
Buenas. No pretendo que se tomen el tiempo de resolverlo pero quizá alguien pueda comprobar si mi resultado es correcto. Lo que hice es trasladar todo para que me queden los puntos P(0,3) y Q(4,5). Con ecuación general de la cfa y esos dos puntos armé un sistema y obtuve una ecuación. Luego igualé y=0 en la ecuación general y el resultado (ecuación de segundo grado), lo utilicé para el discriminante (igualado a 0 por ser tangente). Ya con eso despejé F en función de D, y sustituí en la primera ecuación (la del sistema). Hallé las raíces de la ecuación resultante con Baskhara y ya a partir de esos dos valores de D, calculé el resto de incógnitas (E y F). Con la ecuación de ambas circunferencias saqué sus centros e hice pitágoras entre los dos centros para obtener las suma de los radios. Me dio 10√15. Dejo el gráfico de Geogebra.
-
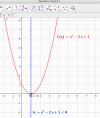
Buenas noches Unicoos. 4ESO, inecuación de segundo grado. La ecuación de 2º grado tiene una sola raíz (+1), pero la inecuación creo que no se verifica para ningún valor.
Un par de cosas:
a) ¿Podéis echarle un vistazo al ejercicio que adjunto en dos imágenes separadas?
b) ¿Se cumple siempre (en desigualdades estrictas) que cuando la ecuación tiene una sola raíz la inecuación no se verifica para ningún valor?

David
el 12/1/20Hola!
En este ejercicio, efectivamente no hay solución que cumpla la desigualdad.
A la respuesta de tu duda b), pues no tiene por qué ser siempre así, como siempre, estudias los intervalos, si se cumplen, hay solución, si no se cumplen, no la hay. Y no hay más. Imagino que ahora irás a por inecuaciones polinómicas, ahora podrás tener desde 3 factores y tendrás que volver a estudiar la respuesta de estos factores. Es lo mismo, pero añadiendo más factores.