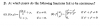-
Hola, Antonio Silvio Palmitano tengo una duda con respecto a un ejercicio en el cual me ayudaste y es, con el inciso c para la gráfica -xy=c el término cruzado me indica una rotación, no? Siendo así tendría que usar las fórmulas de transformación para poder realizar la gráfica? Adjunto foto de lo que hice ya que en mi libro viene la respuesta y no entendía el porque de las "parábolas" que se ven en la gráfica y por lo que veo tienen un ángulo de rotación




Antonio Silvio Palmitano
el 13/1/20Si te piden presentar la ecuación de la superficie gráfica de la función, es tal cuál dices, ya que a la función cuya expresión es: f(x,y) = -x*y, le corresponde una gráfica que es un paraboloide hiperbólico rotado.
Pero, como en tu ejercicio solamente te pedían identificar a la familia de curvas de nivel, es razonable presentar la respuesta tal como lo hemos hecho en tu entrada anterior.
Espero haberte ayudado.
-
$ESO Ruffini
Tengo una duda. ¿Se puede utilizar Ruffini para hallar las raíces de una operación sin término independiente? Por ejemplo
esta: 2x³ - 9x² - 5x
Gracias.

David
el 13/1/20Buenas
Si no te das cuenta que se puede hacer una factorización previa, que es agrupar la x menos que se repita en el polinomio (en este caso x), se procede así:
2 -9 -5 0, y operas como siempre.
Si hago la factorización, pues x(2x^2-9X-5), y hago Ruffini del paréntesis, y x ya es un factor.
-
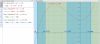 4ESO- resolver 2 inecuaciones dadas a partir de una gráfica.
4ESO- resolver 2 inecuaciones dadas a partir de una gráfica.El ejercicio dice literalmente: “utilizar la gráfica del polinomio P(x) = x³ + 6x² - x +30 para resolver las inecuaciones a) x³ + 6x² - x +30 > 0 y b) x³ + 6x² - x +30 ≤ 50”.
El primer paso dado (como venía haciendo hasta ahora) ha sido intentar averiguar, por Ruffini, las posibles raíces que igualaran a cero la ecuación que indicada. No he conseguido nada, ni siquiera la única raíz (≈ -6,8) que sé que existe porque me la ha dado Geogebra (GG). Las dos inecuaciones tienen solución gráfica e intervalos, como veréis en la imagen adjunta, pero no sé como conseguir las soluciones que me da GG. Os agradezco la ayuda. Buenas noches.


David
el 29/1/20Te dice, "utilizando la grafica". No necesitas resolver ninguna ecuacion.
x³ + 6x² - x +30 > 0 para todos los valores de x cuya imagen es positiva. La solucion sería x>-6.8 o expresada de otra forma (-6.8 , ∞)
Y para x³ + 6x² - x +30 ≤ 50, la solución sería (-∞, -5.53) U ( -2.15 , 1.68) -
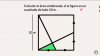
Hola, me ayudarían? Lo que no tengo muy muy claro es, si las condiciones de x=-1, x=0 y x=1 son los puntos de origen de la gráfica o si todas partes del origen en sus respectivos planos xz y yz. Perdón si es que hice una gráfica que ni al caso.





Antonio Silvio Palmitano
el 13/1/20Vamos con una orientación.
Tienes la expresión de la función de dos variables:
f(x,y) = 9*x2 + y2,
cuya gráfica es un paraboloide elíptico, con vértice: V(0,0,0), y eje de simetría OZ positivo, cuya ecuación cartesiana es:
z = 9*x2 + y2 (1) (te dejo la tarea de esbozar esta gráfica.
a)
Planteas la ecuación general de las curvas de nivel de la función:
f(x,y) = k, reemplazas la expresión señalada (1) en el primer miembro, y queda:
9*x2 + y2 = k, con k ∈ R,
observa que en el primer miembro de esta última ecuación tienes una suma de términos positivos, por lo que puedes presentar a la familia de curvas de nivel de la función en la forma:
9*x2 + y2 = k (2), con k ∈ R, k ≥ 0,
que es la ecuación general de una familia de elipses con centro de simetría en el origen de coordenadas del plano OXY, o de un plano paralelo al mismo;
luego, reemplazas los valore correspondientes de la función en el segundo miembro de la ecuación señalada (2), y queda:
i)
9*x2 + y2 = 0,
que corresponde al origen de coordenadas del plano OXY (en este caso tienes una elipse degenerada a su centro de simetría);
ii)
9*x2 + y2 = 1, que puedes escribir en la forma:
9*x2/1 + y2 = 1, divides por 9 en el numerador y en el denominador del primer miembro, y queda:
x2/9 + y2 = 1,
que es la ecuación de una elipse con centro de simetría en el origen de coordenadas del plano paralelo al plano OXY cuya ecuación es: z = 1, con semieje mayor cuya longitud es: a = 3 incluido en el eje OX de dicho plano, y con semieje menor: b = 1 incluido en el eje OY de dicho plano;
iii)
9*x2 + y2 = 9, divides por 9 en todos los términos de esta ecuación, y queda:
x2 + y2/9 = 1,
que es la ecuación de una elipse con centro de simetría en el origen de coordenadas del plano paralelo al plano OXY cuya ecuación es: z = 9, con semieje mayor cuya longitud es: a = 3 incluido en el eje OY de dicho plano, y con semieje menor: b = 1 incluido en el eje OX de dicho plano.
b)
Reemplazas los valores de las abscisas indicadas en la expresión de la gráfica de la función señalada (1), y queda:
i)
z = 9*(-1)2 + y2, resuelves el término numérico, ordenas términos, y queda:
z = y2 + 9,
que es la ecuación de una parábola con vértice (0,9), incluida en el plano paralelo al plano OYZ, cuya ecuación es: x = -1;
ii)
z = 9*12 + y2, cancelas el término nulo, y queda:
z = y2,
que es la ecuación de una parábola con vértice en el origen de coordenadas, incluida en el plano paralelo al plano OYZ, cuya ecuación es: x =0;
iii)
z = 9*12 + y2, resuelves el término numérico, ordenas términos, y queda:
z = y2 + 9,
que es la ecuación de una parábola con vértice (0,9), incluida en el plano paralelo al plano OYZ, cuya ecuación es: x =1.
c)
Reemplazas los valores de las ordenadas indicadas en la expresión de la gráfica de la función señalada (1), y queda:
i)
z = 9*x2 + (-1)2, resuelves el término numérico, ordenas términos, y queda:
z = 9*x2 + 1,
que es la ecuación de una parábola con vértice (0,1), incluida en el plano paralelo al plano OYZ, cuya ecuación es: y = -1;
ii)
z = 9*x2 + 02, cancelas el término nulo, y queda:
z = 9*x2,
que es la ecuación de una parábola con vértice en el origen de coordenadas, incluida en el plano paralelo al plano OXZ, cuya ecuación es: y = 0;
iii)
z = 9*x2 + 12, resuelves el término numérico, ordenas términos, y queda:
z = 9*x2 + 1,
que es la ecuación de una parábola con vértice (0,1), incluida en el plano paralelo al plano OXZ, cuya ecuación es: y =1.
Espero haberte ayudado.