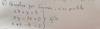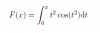-


Yauset Cabrera
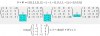
el 12/1/20Resulta que el sistema está integrado por ecuaciones equivalentes, es decir: todos los coeficientes se ven multiplicados por un único número real. Por ejemplo, para obtener la segunda ecuación, multiplicas por dos la primera y ya la tienes. En este caso, el rango de la matriz ampliada que describe el sistema es uno, por lo que nos podemos quedar con una única ecuación para dar solución al sistema. Escogiendo la primera ecuación, y llamando y=t∈ℛ ; z=ξ∈ℛ; se tiene que las soluciones al sistema se expresan como:
(x,y,z)=(1-t-ξ, t, ξ) ; (t,ξ)∈ℛ^2
Espero haberte ayudado ;)
-
¿Como habría que plantear el siguiente ejercicio y cuál es su solución? El enunciado es algo confuso, en especial lo de "y su producto sea máximo"



Antonio Silvio Palmitano
el 12/1/20Puedes comenzar por designar: x, y, z, a los tres números enteros positivos que debes determinar.
Luego, tienes que la suma de los tres números es igual a sesenta, por lo que puedes plantear la ecuación:
x + y + z = 60, y de aquí despejas:
z = 60 - x - y (1).
Luego, tienes que el segundo número es igual al doble del primero, por lo que puedes plantear la ecuación:
y = 2*x (2);
luego, sustituyes la expresión señalada (2) en la ecuación señalada (1), y queda:
z = 60 - x - 2*x, reduces términos semejantes, y queda:
z = 60 - 3*x (3).
Luego, planteas la expresión del producto de los tres números enteros, y queda:
P = x*y*z, sustituyes las expresiones señaladas (2) (3), y queda:
P = x*(2*x)*(60 - 3*x), resuelves la multiplicación de los dos primeros factores, y queda:
P = 2*x2*(60 - 3*x), distribuyes, y queda:
P(x) = 120*x2 - 6*x3 (4),
que es la expresión del producto de los tres números enteros en función del menor de ellos,
y observa que esta expresión corresponde a una función continua y derivable.
Luego, planteas las expresión de la función derivada, y queda:
P'(x) = 240*x - 18*x2 (5);
luego, planteas la condición de valor estacionario (posible mínimo o posible máximo de la función), y queda:
P'(x) = 0, sustituyes la expresión señalada (5), y queda:
240*x - 18*x2 = 0, divides en ambos miembros por -6, ordenas términos, y queda:
3*x2 - 40*x = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
x = 0, que al reemplazar y resolver en las ecuaciones señaladas (2) (3) conduce a: y = 0, z = 60,
y al evaluar la expresión de la función producto señalada (4) queda: P(0) = 0;
2°)
x = 40/3, que al reemplazar y resolver en las ecuaciones señaladas (2) (3) conduce a: y = 80/3, z = 20,
y al evaluar la expresión de la función producto señalada (4) queda: P(40/3) = 64000/9;
luego, observa que tienes que la función producto alcanza su valor máximo (64000/9), para el valor x = 40/3 ≅ 13,333, que no es un valor entero.
Luego, estudias el problema para los dos números enteros más cercanos valor estacionario, y tienes dos opciones:
a)
x = 13,
reemplazas en la ecuación señalada (2), resuelves, y queda:
y = 26,
reemplazas estos dos valores en la ecuación señalada (1), resuelves, y queda:
z = 21;
luego, evalúas la expresión dela función producto señalada (1) para el valor remarcado, y queda:
P(13) = 7098 (6);
b)
x = 14,
reemplazas en la ecuación señalada (2), resuelves, y queda:
y = 28,
reemplazas estos dos valores en la ecuación señalada (1), resuelves, y queda:
z = 18;
luego, evalúas la expresión dela función producto señalada (1) para el valor remarcado, y queda:
P(14) = 7056 (7).
Luego, comparas los valores que toma la función producto señalados (6) (7), y puedes concluir que los tres números enteros positivos que cumplen las condiciones de tu enunciado son:
x = 13, y = 26, z = 21,
y que su producto es:
P(13) = 7098,
que es el máximo posible para tres números enteros positivos que cumplan las condiciones de tu enunciado.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 12/1/20Completas términos en las ecuaciones, y el sistema de tu enunciado queda:
3x + 1y + 0z = 7,
0x + 2y - 2z = 0,
1x + 1y - 1z = 2;
que es un sistema de tres ecuaciones lineales, de primer grado, y con tres incógnitas.
Luego, planteas la expresión del determinante de este sistema, y queda:
D =
3 1 0
0 2 -2
1 1 -1,
resuelves este determinante (por ejemplo desarrollándolo según su primera fila, o aplicando la Regla de Sarrus), y queda:
D = -2 ≠ 0,
por lo que tienes que el sistema es compatible determinado y admite solución única.
Luego, planteas el determinante asociado a la incógnita x, y queda:
Dx =
7 1 0
0 2 -2
2 1 -1,
resuelves este determinante (por ejemplo desarrollándolo según su primera fila, o aplicando la Regla de Sarrus), y queda:
Dx = -4.
Luego, planteas el determinante asociado a la incógnita y, y queda:
Dy =
3 7 0
0 0 -2
1 2 -1,
resuelves este determinante (por ejemplo desarrollándolo según su segunda fila, o aplicando la Regla de Sarrus), y queda:
Dy = -2.
Luego, planteas el determinante asociado a la incógnita z, y queda:
Dz =
3 1 7
0 2 0
1 1 2,
resuelves este determinante (por ejemplo desarrollándolo según su segunda fila, o aplicando la Regla de Sarrus), y queda:
Dz = -2.
Luego, planteas la expresión de la solución del sistema, y queda:
x = Dx/D, reemplazas valores, y queda: y = -4/(-2), resuelves, y queda: x = 2,
y = Dy/D, reemplazas valores, y queda: y = -2/(-2), resuelves, y queda: y = 1,
z = Dz/D, reemplazas valores, y queda: z = -2/(-2), resuelves, y queda: z = 1.
Espero haberte ayudado.
-
Hola alguien me podría ayudar con este problema de serie de McLaurin ?
Mi suposición es que primero consigues la derivada con el Teorema Fundamental del Cálculo, y F(0) = 0. Pero igual no se como conseguir el patron de la serie en 'n'.
Cualquier ayuda es muy agradecida.


Antonio Silvio Palmitano
el 12/1/20Vamos con una orientación.
Aplicas el Teorema Fundamental del Cálculo Integral, y queda:
F'(x) = x2*cos(x2) (1).
Luego, observa que el primer factor corresponde a una expresión monómica desarrollada alrededor de x0 = 0.
Luego, planteas la expresión del desarrollo de Mc Laurin para la función coseno, y queda:
cos(w) = ∑(k=0,+∞) [(-1)k/(2k)!]*w2k;
luego, aplicas la sustitución (cambio se variable): w = x2, y queda:
cos(x2) = ∑(k=0,+∞) [(-1)k/(2k)!]*(x2)2k,
resuelves el exponente en el último factor del argumento de la suma infinita, y queda:
cos(x2) = ∑(k=0,+∞) [(-1)k/(2k)!]*x4k (2).
Luego, sustituyes la expresión señalada (2) en el segundo factor de la expresión señalada (1), y queda:
F'(x) = x2*∑(k=0,+∞) [(-1)k/(2k)!]*x4k,
introduces el factor común (x2) en la suma infinita, asocias factores semejantes en su argumento, y queda:
F'(x) = ∑(k=0,+∞) [(-1)k/(2k)!]*x4k+2 (3),
que es la expresión de la serie de Mc Laurin correspondiente a la derivada de la función cuya expresión tienes en tu enunciado.
Luego, queda que integres, y observa que hemos trabajado con una suma infinita.
Espero haberte ayudado.