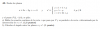-
Hola, mi pregunta puede parecer extraña, soy una persona que dejó las matemáticas hace tiempo, y desde entonces cuando miro un libro miro media página y lo cierro, me gustaría empezar por bachillerato pero no entiendo casi nada, sé que debería empezar por 2º de ESO o así pero en esos libros hay cosas que no hacen falta saber, a ver si algun profesor me indica un método de estudio que me acaben gustando y principalmente entendiéndolas, se lo agradecería mucho, un saludo.
-


Antonio Silvio Palmitano
el 12/1/20Vamos con una orientación.
7)
a)
Planteas la ecuación general de las curvas de nivel de una función de dos variables, y queda:
f(x,y) = k, con k ∈ R;
luego, sustituyes la expresión de la función que tienes en tu enunciado, y queda:
x - y + 2 = k, restas x y restas 2 en ambos miembros, y queda:
-y = -x - 2 + k, multiplicas en todos los términos por -1, y queda:
y = x + 2 - k, asocias los dos últimos términos, y queda:
y = x + (2 - k), con k ∈ R,
que es la ecuación general de una familia de rectas paralelas, cuya pendiente es: m = 1, y cuyas ordenadas al origen quedan expresadas: b = 2 - k;
luego, solo queda que des valores a la indeterminada k para obtener las ecuaciones de algunas de las rectas, y luego graficarlas (te dejo la tarea).
b)
Planteas la ecuación general de las curvas de nivel de una función de dos variables, y queda:
f(x,y) = k, con k ∈ R;
luego, sustituyes la expresión de la función que tienes en tu enunciado, y queda:
x2 + 4y2 = k (1),
que es la ecuación general de las curvas de nivel de la función,
y observa que k es un número positivo, ya que es igual a la suma de dos términos positivos, por lo que tienes la condición: k ≥ 0;
luego, observa que tienes dos opciones:
1°)
si k = 0, reemplazas en la ecuación general señalada (1), y queda:
x2 + 4y2 = 0, que es una ecuación cuadrática homogénea, cuya solución única es: {(0,0)}, ya que la única forma que tienes para que una suma de términos positivos sea igual a cero, es que ambos términos sean iguales a cero, por lo que tienes que en este caso la ecuación conduce al origen de coordenadas;
2°)
k > 0, divides por k en todos los términos de la ecuación general señalada (1), y queda:
x2/k + 4y2/k = 1, divides por 4 al numerador y al denominador del segundo término, y queda:
x2/k + y2/(k/4) = 1,con k ∈ R y k > 0,
que es la ecuación canónica general de una familia de elipses, cuyo centro de simetría es el origen de coordenadas, cuyos ejes mayores tiene la expresión: a = √(k), y cuyos semiejes menores tienen la expresión: b = √(k/4);
luego, solo queda que des valores a la indeterminada k para obtener las ecuaciones de algunas de las elipses, y luego graficarlas (te dejo la tarea).
c)
Planteas la ecuación general de las curvas de nivel de una función de dos variables, y queda:
f(x,y) = k, con k ∈ R;
luego, sustituyes la expresión de la función que tienes en tu enunciado, y queda:
-x*y = k, multiplicas por -1 en ambos miembros, y queda:
x*y = -k (1),
que es la ecuación general de las curvas de nivel de la función;
luego, observa que tienes dos opciones:
1°)
si k = 0, reemplazas en la ecuación general señalada (1), y queda:
-x*y = 0, multiplicas en ambos miembros por -1, y queda:
x*y = 0, y por anulación de una multiplicación, tienes dos opciones:
i)
x = 0, que corresponde al eje coordenado OY,
y = 0, que corresponde al eje coordenado OX;
2°)
k ≠ 0, multiplicas por -1 en ambos miembros de la ecuación general señalad (1), y queda:
x*y = -k ,con k ∈ R y k ≠ 0,
que es la ecuación cartesiana general de una familia de hipérbolas, cuyo centro de simetría es el origen de coordenadas, y cuyas asíntotas son los ejes coordenados;
luego, solo queda que des valores a la indeterminada k para obtener las ecuaciones de algunas de las elipses, y luego graficarlas (te dejo la tarea).
Espero haberte ayudado.
-
¿Me podrían explicar este problema de interés simple. Un capital junto con sus intereses simples al 7% durante 6 años se transforma en 11360 euros. ¿Cual era ese capital? Sé que la fórmula es Interés= C*r*t (años), pero los 11360 euros son el monto y me faltaría un dato para poder depejar.
Gracias. -

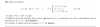 No lo entiendo, yo hice el producto vectorial con i j y k y esto no me sale. Alguien puede ayudarme a comprender esto por fa. Muchas gracias
No lo entiendo, yo hice el producto vectorial con i j y k y esto no me sale. Alguien puede ayudarme a comprender esto por fa. Muchas gracias 

Jose Ramos
el 11/1/20Hay un error en la resolución del ejercicio: Uno de los vectores del plano es (1, -1, 1) que son los coeficientes de µ. Sin embargo, cuando va a pasar de ecuaciones paramétricas a cartesianas el plano, toma en el determinante la columna 1, -1, -1.
Te envío el ejercicio resuelto correctamente con los datos del enunciado:
-
-
Se considera el servicio técnico de una determinada empresa donde de los 50 trabajadores que lo componen, 10 tienen contratado un seguro de vida. ¿Cuál es la probabilidad de que, al seleccionar al azar 5 personas del servicio, haya al menos 2 con seguro?
X e b(n=5,p=10/50)
P(X mayor igual a 2) = 1 - Suma de probabilidad hasta 1


Antonio Silvio Palmitano
el 11/1/20Has planteado bien la expresión de la probabilidad que te piden calcular en el enunciado del problema:
p(X ≥ 2) = 1 - p(X < 1) = 1 - [p(X = 0) + p(X = 1)] (1).
Luego, si consideras que los trabajadores son seleccionados con orden y sin repetición, tienes las probabilidades:
a)
debes elegir cinco trabajadores entre cincuenta, y que no tengan contratado un seguro:
p(X = 0) = (40/50)*(39/49)*(38/48)*(37/47)*(36/46) ≅ 0,310563;
b)
debes elegir cinco trabajadores entre cincuenta, y que uno de ellos sí tenga contratado un seguro (observa que tienes cinco opciones para ubicar al trabajador asegurado):
p(X = 1) = 5*(10/50)*(40/49)*(39/48)*(38/47)*(37/46) ≅ 0,422534.
Luego, reemplazas valores en la expresión señalada (1), y queda:
p(X ≥ 2) ≅ 1 - [0,310563 + 0,422534] ≅ 1 - 0,733097 ≅ 0,266903.
Espero haberte ayudado.
-
Duda sobre integrales, por coordenadas esféricas:
∫∫∫e^-√((x^2 + y^2 +z^2)^3) dxdydz. El recinto para la función es R3, al pasarlo a coordenadas esféricas queda
∫∫∫ e^(-1 / √(p^6))) * p^2*sen(phi) dO dphi dp ;
p^2*sen(phi) lo pongo al ser el jacobiano, estoy definiendo la integral correspondiente a dp entre 0 y 1 porque loslimites de e^(-1 / √(p^6)) son: 1 al ir a 0, y 0 al ir a +- infinito.en el desarrollo de las integrales me surgen dudas, ¿estoy poniendo mal los límites de la región también?


Antonio Silvio Palmitano
el 11/1/20Tienes la integral triple:
∫∫∫R³ e-√[(x²+y²+z²)³]*dx*dy*dz = ∫∫∫R³ e-√(ρ˄6)*ρ2*senφ*dρ*dφ*dθ,
aquí simplificas la potencia y la raíz en el exponente del primer factor en el argumento de la integral, y queda:
∫∫∫R³ e-√[(x²+y²+z²)³]*dx*dy*dz = ∫∫∫R³ e-ρ³*ρ²*senφ*dρ*dφ*dθ,
con los intervalos de integración:
0 ≤ ρ < +∞ (que expresado en forma estricta queda: ρ > 0),
0 ≤ φ ≤ π,
0 ≤ θ < 2π;
y observa que la integral para la variable ρ es impropia, y que para resolverla puedes aplicar la sustitución (cambio de variable): w = ρ3.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.










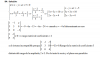
 No podríamos hacer el producto escalar de el normal y el director y sacar el valor de a (yo hice eso, pero veo que el ejercicio aún sigue y no lo entiendo jeje) ayuda muchas gracias!!
No podríamos hacer el producto escalar de el normal y el director y sacar el valor de a (yo hice eso, pero veo que el ejercicio aún sigue y no lo entiendo jeje) ayuda muchas gracias!!