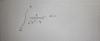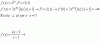-


Antonius Benedictus
el 10/1/20Primera observación: y=x^(3x) SOLO está definida en x>0. Para que el punto (0,1) esté en ella hay que redefinirla.
Segunda: una vez hecho esto, se puede hablar SOLO de semitangente por la derecha (que va a resultar ser vertical, pues la función no resulta derivable en x=0, pues tiene derivada infinita)
-
-
Hola todos, alguno me podría ayudar con el siguiente ejercicio, la respuesta dice que PC= 18 y CD=15, ojala alguno pueda ayudarme con el ejercicio paso a paso porque la verdad no entiendo el procedimiento que se utilizo para llegar a esa respuesta, gracias de antemano.
-
 A mi me sale 90 grados. Estaría bien? Porque 90 significa que son perpendiculares, y para que se cumpla el vectorial deberían ser 90 grados, si no me equivoco... Gracias!!
A mi me sale 90 grados. Estaría bien? Porque 90 significa que son perpendiculares, y para que se cumpla el vectorial deberían ser 90 grados, si no me equivoco... Gracias!!

Antonio Silvio Palmitano
el 9/1/20Recuerda la expresión del módulo del producto vectorial de dos vectores no nulos:
|u x v| = |u|*|v|*senθ,
y observa que para que esta expresión sea igual a cero, entonces debe cumplirse la condición:
senθ = 0, aquí compones en ambos miembros con la función inversa del seno, y queda:
θ = 0°, lo que corresponde a que los vectores u y v son paralelos,
y observa que para este ángulo tienes que su coseno es igual a 1, que es lo que han obtenido como conclusión en el desarrollo que tienes al comienzo de la última línea en tu figura.
Espero haberte ayudado.
-
 Buenas necesito ayuda para resolver la parte c y d de este ejercicio.
Buenas necesito ayuda para resolver la parte c y d de este ejercicio.Cuando realizo la derivada con respecto a x y con respecto y y sustituyo los valores (0,0) en cada una me queda una indeterminación 0/0 y cuando intento hacer los limites me pasa lo mismo:
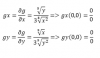
No se que hacer para que no me quede esa indeterminación.


Antonio Silvio Palmitano
el 9/1/20Observa que la función es continua en R2, y que su valor en el punto O(0,0) es: g(0,0) = 0.
Observa que con las reglas de derivación que has aplicado has obtenido las expresiones de las funciones derivadas parciales:
gx(x,y) = ∛(y)/(3*∛[x2]), que está definida en el conjunto: R2 - {x = 0};
gy(x,y) = ∛(x)/(3*∛[y2]), que está definida en el conjunto: R2 - {y = 0}.
Luego, observa que estas expresiones no informan sobre la existencia de las derivadas parciales en el punto O(0,0), por lo que debes plantearlas por medio de la definición de derivada parcial en en un punto:
gx(0,0) = Lím(h→0) [g(0+h,0) - g(0,0)]/h = Lím(h→0) [∛(h*0) - ∛(0*0)]/h = Lím(h→0) [∛(0) - ∛(0)]/h = Lím(h→0) [0/h] = 0,
gy(0,0) = Lím(k→0) [g(0,0+k) - g(0,0)]/k = Lím(k→0) [∛(0*k) - ∛(0*0)]/k = Lím(k→0) [∛(0) - ∛(0)]/k = Lím(k→0) [0/h] = 0,
por lo que tienes que las dos derivadas parciales de la función están definidas en el origen, y toma cada una el valor que hemos remarcado.
Luego, para estudiar la continuidad de la función derivada parcial con respecto a x en el punto O(0,0), observa que si estudias la expresión que tú has obtenido para las trayectorias rectas que pasan por el punto en estudio, cuya ecuación cartesiana general es: y = m*x, tienes:
L = Lím(x→0) [∛(m*x)/(3*∛[x2])] = (1/3)*Lím(x→0) [∛(m*x)/∛[x2]] = (1/3)*Lím(x→0) [∛(m*x/x2)] = (1/3)*Lím(x→0) [∛(m/x)] = ±∞,
por lo que tienes que la función derivada parcial con respecto a x no es continua en el punto en estudio.
Luego, queda para ti que demuestres con un procedimiento similar puedes demostrar que la función derivada parcial con respecto a y no es continua en el punto en estudio.
Luego, queda que plantees la definición de diferenciabilidad de la función para el punto en estudio: O(0,0), a fin de demostrar que la misma no es diferenciable en dicho punto (te dejo la tarea).
Espero haberte ayudado.