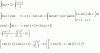-
¿Por qué z(0,0,1)? si la columna de z está vacío no entiendo por qué esta respuesta es válida.
-2x+2y=0
2x+y=0
3y=0
y=0
Por lo tanto x sería también 0. Pero no le encuentro lugar a z


Jose Ramos
el 8/1/20Al desaparecer z del proceso, z no está condicionado por ninguna relación, por eso puede valer cualquier valor real, de ahí que las soluciones sean x = 0, y = 0, z = α, siendo α cualquier número real.
Las soluciones (0,0,α) = α (0,0,1) de ahí que (0,0,1) sea un generador de las soluciones del sistema.
-
Hola a todos, alguno me podría decir el procedimiento que se hizo para obtener que y=4/3(cuatro tercios) , z=8/3(ocho tercios)??? sabiendo que x=2.25. Espero que alguno lo pueda solucionar paso a paso, gracias de antemano.
-

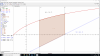
 quisiera saber si el ejercicio 29 esta bien realizado,otra consulta,los vectores directores no son proporcionales y por lo tanto no son paralelos,quisiera saber si es correcto y como puedo saber si se intersectan o son alabeadas,creo buscaria la interseccion y listo,no afecta el producto vectorial creo,desde ya gracias.
quisiera saber si el ejercicio 29 esta bien realizado,otra consulta,los vectores directores no son proporcionales y por lo tanto no son paralelos,quisiera saber si es correcto y como puedo saber si se intersectan o son alabeadas,creo buscaria la interseccion y listo,no afecta el producto vectorial creo,desde ya gracias.

Jose Ramos
el 8/1/20Al final, dentro del valor absoluto es - 20 porque la ecuación del plano es -5x + 5y +5z - 20 = 0. El proceso está perfecto. Salvando ese error al final, el resultado correcto es √3.
Con respecto a la segunda pregunta, se supone que si el enunciado te dice que las rectas determinan un plano y los vectores no son proporcionales es que las rectas son secantes, pero siempre puedes comprobar previamente su posición relativa.
-


Breaking Vlad
el 8/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
hola como es tan ? tengo una duda de un ejercicio que no recuerdo como resolver , si alguien me podría ayudar se lo agradecería muchísimo . 1) ¿para que conjunto de valores de xeR es un entero de expresión 1/3(x+1) ? muchas gracias


Antonio Silvio Palmitano
el 8/1/20Veamos dos situaciones, y tú elige la que corresponde a tu enunciado.
1°)
Si la expresión de tu enunciado es: 1/[3*(x + 1)], entonces puedes plantear la ecuación:
1/[3*(x + 1)] = n, con n ∈ Z, multiplicas por 3 en ambos miembros, y queda:
1/(x + 1) = 3*n, multiplicas por (x + 1) y divides por 3*n en ambos miembros, y queda:
1/[3*n] = x + 1, restas 1 en ambos miembros, y luego despejas:
x = 1/[3*n] - 1 (observa que n no puede tomar el valor cero),
por lo que puedes concluir que el conjunto solución queda expresado:
S1 = { x ∈ R / x = 1/[3*n] - 1, n ∈ Z, n ≠ 0 }.
2°)
Si la expresión de tu enunciado es: (1/3)*(x + 1), entonces puedes plantear la ecuación:
(1/3)*(x + 1) = n, con n ∈ Z, multiplicas por 3 en ambos miembros, y queda:
x + 1 = 3*n, restas 1 en ambos miembros, y queda:
x = 3*n - 1 (observa que n puede tomar cualquier valor entero),
por lo que puedes concluir que el conjunto solución queda expresado:
S2 = { x ∈ R / x = 3*n - 1, n ∈ Z }.
Espero haberte ayudado.