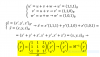-
David Poyatos
el 17/11/18Hola, cómo se plantearian las ecuaciones del ejercicio 8 b, alguien podría ayudarme. Gracias
Antonio
el 17/11/18Sea p el precio de cada billete con destino europeo comunitario.
El mayorista vende en total 30 billetes a destinos nacionales a 240 € cada uno, 20 billetes a destinos europeos comunitarios a un precio de p € cada uno y 30 billetes a destinos internacionales no comunitarios a 500 € cada uno obteniendo por la venta de todos ellos 32000€, es decir:
30*240+20p+30*500=32000
resolviendo
p=490€
Por lo que cada billete de 400€ lo tiene que subir a 490€, que corresponde a un incremento de 22.5%
-
Nerea Cerdeira Fernandez
el 17/11/18 -
comando bachuerino
el 17/11/18Hola buenas, si tengo un conjunto de vectores, hay una manera facil de calcular el numero de vectores linealmente independientes que hay en el conjunto?
Por ejemplo, en este conjunto:
(1,1,1) (0,2,1)(2,0,-3)(-1,1,2)
-
Bernardo
el 17/11/18 -
Bernardo
el 17/11/18 -
Bernardo
el 17/11/18 -
Víctor López
el 17/11/18 -
Bernardo
el 17/11/18 -
Ane
el 17/11/18 -
David Poyatos
el 16/11/18Hola, cómo se haría el siguiente ejercicio, es que no sé cómo plantear las ecuaciones de cambio de base
Antonius Benedictus
el 16/11/18
Antonio Silvio Palmitano
el 16/11/18Te ayudo.
Plantea la expresión de un vector genérico (P) como combinación lineal de los elementos de la base B', y queda:
a*u' + b*v' + C*w' = P (1),
sustituyes las expresiones de los vectores en el primer miembro de la ecuación señalada (1), y queda:
a*(u+v+w) + b*(u+v) + c*(u+w) = P,
distribuyes en todos los términos del primer miembro, extraes factores comunes vectoriales, y queda:
(a+b+c)*u + (a+b)v + (a+c)*w = P (2).
Luego, vamos por pasos:
1)
Planteas la condición: P = u, sustituyes en el segundo miembro de la ecuación vectorial señalada (2), y queda:
(a+b+c)*u + (a+b)*v + (a+c)*w = u;
luego, como los vectores u, v y w son linealmente independientes, tienes que los factores escalares del primer miembro quedan:
a + b + c = 1,
a + b = 0,
a + c = 0:
luego, resuelves este sistema (te dejo la tarea), y su solución queda: a = -1, b = 1, c = 1,
reemplazas estos valores y la expresión vectorial remarcada en la ecuación vectorial señalada (1), y queda:
-u' + v' + w' = u,
que es la expresión del primer vector de la base B como combinación lineal de los elementos de la base B'.
2)
Planteas la condición: P = v, sustituyes en el segundo miembro de la ecuación vectorial señalada (2), y queda:
(a+b+c)*u + (a+b)*v + (a+c)*w = v;
luego, como los vectores u, v y w son linealmente independientes, tienes que los factores escalares del primer miembro quedan:
a + b + c = 0,
a + b = 1,
a + c = 0:
luego, resuelves este sistema (te dejo la tarea), y su solución queda: a = 1, b = 0, c = -1,
reemplazas estos valores, cancelas el término nulo, y la expresión vectorial remarcada en la ecuación vectorial señalada (1), y queda:
u' - w' = v,
que es la expresión del segundo vector de la base B como combinación lineal de los elementos de la base B'.
3)
Planteas la condición: P = w, sustituyes en el segundo miembro de la ecuación vectorial señalada (2), y queda:
(a+b+c)*u + (a+b)*v + (a+c)*w = w;
luego, como los vectores u, v y w son linealmente independientes, tienes que los factores escalares del primer miembro quedan:
a + b + c = 0,
a + b = 0,
a + c = 1:
luego, resuelves este sistema (te dejo la tarea), y su solución queda: a = 1, b = -1, c = 0,
reemplazas estos valores, cancelas el término nulo, y la expresión vectorial remarcada en la ecuación vectorial señalada (1), y queda:
u' - v' = w,
que es la expresión del tercer vector de la base B como combinación lineal de los elementos de la base B';
por lo que tienes que las expresiones de los vectores de la base B como combinaciones lineales de los vectores de la base B' quedan:
u = -u' + v' + w',
v = u' - w',
w = u' - v'.
Luego, tienes en tu enunciado las expresiones de los vectores de la base B' como combinaciones lineales de los vectores de la base B:
u' = u + v + w,
v' = u + v,
w' = u + w.
Espero haberte ayudado.
