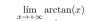-
Hola! Alguien podría ayudarme con el siguiente ejercicio:
Dar las soluciones en forma exponencial de la siguiente ecuación z5 = 1 .
Gracias!


Antonio Silvio Palmitano
el 1/1/20Tienes la ecuación de tu enunciado:
z5 = 1, expresas el segundo miembro en forma exponencial general, y queda:
z5 = 1*ei*2*k*π, con k ∈ Z, extraes raíz quinta en ambos miembros, y queda:
zk = 5√(1*ei*2*k*π), con k ∈ Z, distribuyes la raíz en el segundo miembro, resuelves el factor real, y queda:
zk = 1*5√(ei*2*k*π), con k ∈ Z, expresas al segundo factor como una potencia, y queda:
zk = 1*ei*2*k*π/5, con k ∈ Z, y 0 ≤ k < 5, de acuerdo con el Teorema Fundamental;
luego, reemplazas valores, y las cinco soluciones de la ecuación de tu enunciado quedan expresadas:
z0 = 1*ei*0 = 1,
z1 = 1*ei*2*π/5,
z2 = 1*ei*4*π/5,
z3 = 1*ei*6*π/5,
z4 = 1*ei*8*π/5.
Espero haberte ayudado.
-


Jose Ramos
el 1/1/20la tangente de un ángulo agudo mide el grado de inclinación de dicho ángulo. Así, la tangente de 0º es 0 porque sería un llano. A medida que vamos elevando el ángulo, la pendiente, es decir la tangente del ángulo, va aumentando, así al llegar a 45º la tangente vale 1. Si aumentamos a 60º la tangente aumenta y vale raiz de 3.... Al llegar a 90º nos encontramos ante un "muro" vertical, por lo que la pendiente es + infinito. De ahí que se diga que la tangente de 90 (pi/2) es + infinito. Como el arctag es la función inversa de la tag, el arctag (+ infinito) es pi/2.
-


Antonio Silvio Palmitano
el 1/1/20Tienes el punto: P0(1,1,1).
Tienes a la recta r presentada como intersección de dos planos, de los cuáles tienes ecuaciones cartesianas implícitas, y observa que los vectores directores de estos planos pueden ser: u1 = < 1 ; 1 ; -1 > y u2 = < 1 ; 2 ; -1 >, respectivamente; luego, puedes plantear que un vector normal a la recta es el producto de los vectores normales a los planos, y queda:
ur = u1 x u2 = < 1 ; 1 ; -1 > x < 1 ; 2 ; -1 > = < 1 ; 0 ; 1 >.
Tienes una ecuación cartesiana implícita del plano π, por lo que tienes que uno de sus vectores normales es: nπ = < 1 ; 1 ; 1 >.
a)
Determinas un punto de la recta, por ejemplo asignando el valor: z = 0, y queda el sistema de ecuaciones:
x + y + 1 = 0,
x + 2y - 1 = 0,
cuya solución (te dejo la tarea de resolver este sistema de ecuaciones) es: x = -3, y = 2,
por lo que tienes el punto: A(-3,2,0) que pertenece a la recta r;
luego, puedes determinar el vector perteneciente al plano buscado:
v = P0A = < -3-1 ; 2-1 ; 0-1 > = < -4 ; 1 ; -1 >;
luego, con este vector, y el vector director de la recta que está incluida en el plano, puedes plantear que el producto vectorial de estos vectores es un vector normal la plano buscado, y queda:
nPl = ur x v = < 1 ; 0 ; 1 > x < -4 ; 1 ; -1 > = < -1 ; -3 ; 1 >;
luego, con las componentes de este vector normal, y con las coordenadas del punto P0(1,1,1) que pertenece al plano buscado, planteas una ecuación cartesiana implícita del plano buscado, y queda:
-1*(x - 1) - 3*(y - 1) + 1*(z - 1) = 0, distribuyes en los tres términos del primer miembro, reduces términos semejantes, y queda:
-x - 3y + z + 3 = 0.
b)
Observa que el vector normal al plano π: nπ = < 1 ; 1 ; 1 > es uno de los vectores de la recta perpendicular buscada, y como tienes que el punto P0(1,1,1) pertenece a ella, puedes plantear sus ecuaciones ecuaciones cartesianas paramétricas, y queda:
x = 1 + λ,
y = 1 + λ,
z = 1 + λ,
con λ ∈ R;
luego, sustituyes estas tres últimas expresiones remarcadas en la ecuación cartesiana implícita del plano π que tienes en tu enunciado, reduces términos semejantes, y queda la ecuación:
3 + 3λ = 1, y de aquí despejas: λ = -2/3, que es el valor del parámetro correspondiente al punto de intersección del plano π con la recta perpendicular a él;
luego, reemplazas este valor del parámetro en las ecuaciones cartesianas paramétricas de la recta perpendicular que tienes remarcadas, resuelves, y queda:
x = 1/3,
y = 1/3,
z = 1/3,
por lo que tienes que la expresión del punto que es intersección entre el plano π y la recta perpendicular a él es: B(1/3,1/3,1/3);
luego, puedes plantear que la distancia entre el punto P y el plano π es igual a la distancia entre el punto P y el punto B, por lo que tienes:
d(P,π) = d(P,B) = √([1/3-1]2 + [1/3-1]2 + [1/3-1]2) = √(4/3) = √(4*3/32) = 2√(3)/3.
c)
Observa que la recta r está contenida en el plano σ, por lo que tienes que su vector director: ur = < 1 ; 0 ; 1 > es un vector de dicho plano;
luego, como tienes que el plano σ contiene a la recta r, entonces tienes que el vector director de la recta r y el vector normal al plano σ, al que planteamos: uσ = < a ; b ; c >, son perpendiculares, por lo que puedes plantear que el producto escalar entre estos vectores es igual a cero, y queda la ecuación vectorial:
ur • uσ = 0, sustituyes las expresiones de los vectores en el primer miembro, y queda:
< 1 ; 0 ; 1 > • < a ; b ; c > = 0, desarrollas el producto escalar, cancelas el término nulo, y queda la ecuación:
a + c = 0, y de aquí despejas: c = -a (1);
luego, como tienes que el plano σ y el plano π son perpendiculares puedes plantear que sus vectores normales son perpendiculares, por lo que puedes plantear la ecuación vectorial:
nπ • uσ = 0, sustituyes las expresiones de los vectores en el primer miembro, y queda:
< 1 ; 1 ; 1 > • < a ; b ; c > = 0, desarrollas el producto escalar, y queda la ecuación:
a + b + c = 0;
luego, sustituyes la expresión señalada (1) en esta última ecuación, reduces términos semejantes, y queda: b = 0 (2);
luego, sustituyes las expresiones señalada (1) (2) en la expresión general de los vectores normales al plano σ, y queda:
uσ = < a ; 0 ; -a >, que para a = 1 conduce al vector: Uσ = < 1 ; 0 ; -1 >;
luego, con la expresión de este último vector, y con el punto A(-3,2,0) que pertenece a la recta y también al plano σ, puedes plantear una ecuación cartesiana implícita de dicho plano, y queda:
1*(x - [-3]) + 0*(y - 2) -1*(z - 0), distribuyes, cancelas términos nulos, reduces términos semejantes, y queda:
x - z + 3 = 0.
Espero haberte ayudado.
-
 No consigo entender esta parte. Yo lo que hice fue considerar el vector director que busco para la recta como el vector normal del plano al ser la recta t el plano perpendiculares, pero la solución no coincide Ayuda porfa, muchas gracias!!!!!
No consigo entender esta parte. Yo lo que hice fue considerar el vector director que busco para la recta como el vector normal del plano al ser la recta t el plano perpendiculares, pero la solución no coincide Ayuda porfa, muchas gracias!!!!!

Jose Ramos
el 31/12/19Importante: La recta pedida está en el plano, por tanto no puede tener como vector director el vector normal del plano. Ese es tu error. Por otra parte al estar en el plano es perpendicular al vector normal al plano y a la recta PQ. De ahí el producto vectorial que hace para obtener un vector perpendicular en esas condiciones.
-


Antonio Silvio Palmitano
el 31/12/19Vamos con una precisión, a partir del desarrollo que propone el colega José.
Observa que el vector normal al plano cuya ecuación cartesiana implícita tienes en tu enunciado es: nπ = < 1 ; -1 ; -1 >, por lo que al plantear la condición de perpendicularidad de la recta buscada con este plano como indica el colega José, queda la ecuación:
a - b - c = 0 (1).
Luego, el colega José ha planteado la condición de perpendicularidad entre la recta cuyas ecuaciones cartesianas simétricas (o continuas) tienes en tu enunciado, y ha quedado la ecuación:
a + 2b - 4c = 0 (2).
Luego, restas la ecuación señalada (1) de la ecuación señalada (2) como indica el colega José, y queda:
3b - 3c = 0, y de aquí despejas: c = b (3);
luego, sustituyes la expresión señalada (3) en las ecuaciones señaladas (1) (2), y de ambas despejas: a = 2b;
luego, tienes que la expresión general de los vectores directores de la recta buscada queda:
ub = < 2b ; b ; b >, con b ∈ R y b ≠ 0, y observa que para b = 1 tienes el vector: u1 = < 2 ; 1 ; 1 >, que es el vector vr que tienes en tu última imagen.
Luego, con en vector director que tienes remarcado, y el punto P(2,-1,-2) que tienes en tu enunciado, planteas las ecuaciones cartesianas paraméticas de la recta buscada, y queda:
x = 2 + 2λ,
y = -1 + λ,
z = -2 + λ,
con λ ∈ R,
como has consignado en tu última imagen.
Espero haberte ayudado.