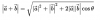Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Utiliza esta fórmula:

gracias, pero sigo sin entenderlo del todo

como lal = 2 => l3al = 6

como lbl = √3 => l-4al = 4√3

l3a-4bl² = l3al² + l-4bl²+2·l3al·l-4bl·cos30º

l3a-4bl² = 6² + (4√3)²+2·6·4√3·cos30º

l3a-4bl² = 36 + 48+48√3·√3/2

l3a-4bl² = 36 + 48+48·3/2

l3a-4bl² = 156

l3a-4bl = √156 = 12.48

Gracias Antonio, 

La fórmula que utilicé es para la suma de vectores, la de la resta es:

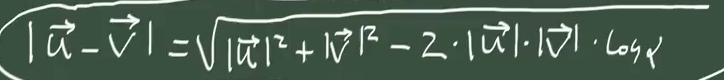
como lal = 2 => l3al = 6

como lbl = √3 => l4bl = 4√3

l3a-4bl2 = l3al2 + l-4bl2-2·l3al·l4bl·cos30º

l3a-4bl2 = 62 + (4√3)2-2·6·4√3·cos30º

l3a-4bl2 = 36 + 48-48√3·√3/2

l3a-4bl2 = 36 + 48-48·3/2

l3a-4bl2 = 12

l3a-4bl = √12 = 3.46

f(x) = log_a (1/x)

¿Podrías detallar los pasos?

¿Cuál es el ejercicio,  Luis?

Es un ejercicio de economía sobre préstamos el cual decía : construir el cuadro de amortización de un préstamo de 2500000 € , el cuál se cancelará con 5 anualidades iguales ( método francés). Tipo de interés 6%anual. Tenía que calcular la anualidad del año 1 que se calcula con esta fórmula ya dada en la imagen adjunta donde c1 sería los 250.000 , i el interés que es el 6% y n los años que son 5

La cuestión es que tenía que hacer esa fórmula pero a muchos compañeros con esos datos no les daba eso. 

Gracias Antonio 

A mí me sale esto:

a) Efectivamente, para k= -1 y k=2 la matriz no es invertible, pues su determinante sería nulo

b) la solución es:

1    -1    3/2

0    0    -1/2

0     1    -1

En el apartado b a mi me sale la ultima columna 1, 1/2 i 1  , he repasado un monton de veces todos los calculos y lo volvi a hacer pero no se donde me equivoco

Muchas grcias Antonio, pero a nosotros no nos han enseñado el método de Gauss porque según mi profesor es mucho más fácil  utilizar la formula Adjunto de la matris transferida dividido por el determinante, yo segui los pasos pero la ultima columna no me da la solucion...

Aquí:

https://matrixcalc.org/es/#%7B%7B1,1,1%7D,%7B0,-2,1%7D,%7B0,-2,0%7D%7D%5E%28-1%29

Marca la opción de "Usando la matriz de adjuntos".

El método de Gauss es más bonito, diga lo que diga tu profe.

Muchas gracias Antonio !!

Estudio completo de una funcion logaritmica

Muchas gracias, Antonio. Pero hay apartados que no están en el vídeo.

a)

- Hay que hallar la superficie del tejado:

Son dos rectángulos idénticos

con base 30 m y ancho  √(8²+3²) = √73 m

S = 30 · √73 m²

- Multiplicamos la superficie del tejado por el precio de reparación de cada metro cuadrado:

Precio = (30 · √73) · 25 = 70√73 = 6408.00 €

b)

- Calcularemos el volumen de la casa:

Para ello calculamos el área de la fachada y la multiplicamos por la profundidad de la casa

V =[15·4 + 1/2 · 15 ·3] · 30 = 2475 m³

lo dividimos entre 165 m³ por aparato

2475/165 = 15 aparatos

http://www.unicoos.com/video/matematicas/1-bachiller/funciones/caracteristicas-basicas/dominio-de-una-funcion

El dominio de una función son los valores de x en la que existe imagen.

a) Si la función tiene denominador hay que eliminar los valores de x que anule al denominador

b) Si la función tiene raíces de índice par hay que eliminar los valores de x que haga al radicando negativo

c) Si la función tiene logaritmos hay que eliminar los valores de x que haga el argumento nulo o negativo

aquí tienes varios ejercicios resueltos para practicar

Revisa las operaciones, Roger: