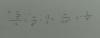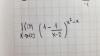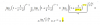-
luz hm
el 2/6/17 -
Santiago Pérez
el 2/6/17Dados los vectores u=(2,-1,3); v=(-3,-2,0) ; W=(-4,1,3x+1)
Hallar, si existen, valores de x para que w.(u x v)=0
hice todas las operaciones, sacando producto vectorial entre u y v y despues es resultado lo multiplique por w y me dio un vector
(-24,-9,-21x-7)=0
y lo iguale a 0 pero nose como seguir, si podrian ayudarme, y verificar si lo que hice esta bien?.
Gracias.
-
Matias Bajac
el 2/6/17 -
Sánchez Miranda Antonio
el 2/6/17 -
Carlos Ojeda
el 1/6/17
-
Jose Sanchez
el 1/6/17Hola! Necesito ayuda con este ejercicio de Matrices
muchas gracias 
Antonius Benedictus
el 2/6/17 -
fernando
el 1/6/17Un tren transporta 560 viajeros que realizan el mismo trayecto. La recaudación del importe de sus
billetes asciende a 39.600 €. Calcula cuántos viajeros han pagado el importe total del billete (90 €),
cuántos se han beneficiado de un descuento del 50% y cuántos han pagado el 60% del precio del
billete, sabiendo que el número de viajeros que ha pagado el billete completo es el triple del que ha
pagado el 60% del mismo.
Antonio
el 1/6/17Antonio
el 1/6/17fernando
el 1/6/17fernando
el 1/6/17Antonio
el 1/6/17Entonces continuamos:
x + y + z = 560
90x+45y+54z=39 600
x=3z
sustituyendo x por 3z obtenemos:
3z + y + z = 560 => y + 4z = 560
90·3z+45y+54z=39 600 => 45y +324z = 39 600
Tenemos por tanto que:
y + 4z = 560
45y +324z = 39 600
ahora tienes dos ecuaciones con dos incógnitas: ¿Sabes resolverlo? Hay varias formas de hacerlo: Sustitución, reducción, igualación.
fernando
el 1/6/17sí gracias, voy a mirarlo y lo hago, la única duda que tengo es cómo se que tengo que hacer sustitucion,reduccion o igualacion? Haga lo que haga siempre me darán en las 3 el mismo resultado?
Estuve haciendo sistemas pero ya me decia de la forma que tenia que hacerlas, pero sin que me lo diga no sé muy bien como detectarlo, si tienes algún consejo .
Antonio
el 1/6/17los métodos de sustitución, reducción e igualación son tres caminos para llegar a la misma solución,
debes elegir el más fácil o uno cualquiera de ellos, da lo mismo.
La gente suele elegir el de reducción.
intenta hacer éste o cualquier otro sistema por los tres métodos, te tiene que dar el mismo resultado y así practicas.
-
leo
el 1/6/17 -
Jon Aginaga
el 1/6/17¡Buenas! ¿Cuál sería la manera para plantear este ejercicio? Quiero decir, el dibujo y cómo debería nombrar cada cosa. Muchas gracias.
Se divide un segmento de longitud 200 cm en dos trozos. Con uno de los trozos se forma un cuadrado y con el otro un rectángulo en el que la base es el doble de la altura. Calcula la longitud de cada uno de los trozos con la condición que la suma de las áreas del cuadrado y del rectángulo sea mínima.
-
Lourdes
el 1/6/17
