-


Breaking Vlad
el 8/1/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)


Antonio Silvio Palmitano
el 9/1/20Establece un sistema de referencia con origen de coordenadas en el punto de partida de la lancha, con eje OX paralelo al río con sentido positivo opuesto al sentido de la corriente, y con eje OY perpendicular a la corriente, con sentido positivo hacia la costa opuesta al punto de partida de la embarcación.
a)
Observa que el punto de partida es: O(0,0), que el punto de llegada es: B(500,1000) m, y que el punto proyección del punto B sobre el eje OX es: A(500,0) m;
luego, planteas la expresión de la tangente del ángulo determinado por los segmentos OA y OB, y queda:
tanθ = |AB|/|OA| = 1000/500 = 2, compones con la función inversa de la tangente, y queda:
θ ≅ 63,435°.
b)
Planteas la expresión de la componente del desplazamiento de la lancha en la dirección del eje OX, y queda:
Δx = |OA| = 500 m,
planteas la expresión de la correspondiente componente de la velocidad de la lancha con respecto a un observador ubicado sobre la tierra en la costa, y queda:
vTx = Δx/Δt = 500/10 = 50 m/min = 50/60 = 5/6 m/s ≅ 0,833 m/s.
Planteas la expresión de la componente del desplazamiento de la lancha en la dirección del eje OY, y queda:
Δy = |AB| = 1 Km = 1000 m,
planteas la expresión de la correspondiente componente de la velocidad de la lancha con respecto a un observador ubicado sobre la tierra en la costa, y queda:
vTy = Δy/Δt = 1000/10 = 100 m/min = 100/60 = 5/3 m/s ≅ 1,667 m/s.
Planteas las componentes de la velocidad de la corriente de agua con respecto a un observador ubicado sobre la tierra en la costa (recuerda que el eje OX es paralelo a esta corriente), y queda:
vAx = a determinar (observa que este valor debe ser negativo, porque el sentido de la corriente es opuesto al sentido positivo del eje OX),
vAy = 0.
Luego, de acuerdo con el Principio de Relatividad de Galileo, planteas las expresiones de la velocidad relativa de la lancha con respecto al agua, y queda:
vrx = vTx - vAx,
vry = vTy - vAy,
sustituyes las expresiones que tienes remarcadas, y queda:
vrx = 5/6 - vAx (1) (en m/s),
vry = 5/3 - 0 = 5/3 m/s (2),
planteas la expresión del módulo de la velocidad de la lancha con respecto al agua (vr),
que según tu enunciado debe ser igual a: 10 Km/h = 25/9 m/s = vr, y queda la ecuación:
√(vrx2 + vry2) = vr, elevas al cuadrado en ambos miembros, y queda:
vrx2 + vry2 = vr2,
sustituyes las expresiones señaladas (1) (2) en el primer miembro, reemplazas el valor del módulo de la velocidad con respecto al agua, y queda:
(5/6 - vAx)2 + (5/3)2 = (25/9)2, restas (5/3)2 en ambos miembros, resuelves el segundo miembro, y queda:
(5/6 - vAx)2 = 400/81, extraes raíz cuadrada en ambos miembros (observa que esta raíz tiene índice par), y queda:
|5/6 - vAx| = 20/9,
y de acuerdo con la definición de valor absoluto, tienes dos opciones:
1°)
5/6 - vAx = -20/9, restas 5/6 en ambos miembros, y luego despejas:
vAx = 55/18 m/s, que no tiene sentido para este problema (recuerda que el sentido de la corriente es opuesto al sentido positivo del eje OX,
2°)
5/6 - vAx = 20/9, restas 5/6 en ambos miembros, y luego despejas:
vAx = -25/18 m/s = -5 Km/h, que sí tiene sentido para este problema.
c)
Planteas las expresiones de las componentes de la velocidad de la lancha con respecto al agua, cuando ésta está quieta, y queda:
vLx = vL*cosθ ≅ (25/9)*cos(63,435°) ≅ 1,242 m/s, a continuación planteas la expresión del intervalo de tiempo correspondiente, y queda:
Δt = Δx/vLx ≅ 500/1,242 ≅ 402,493 s ≅ 6 min 42,493 s;
vLy = vL*senθ ≅ (25/9)*sen(63,435°) ≅ 2,485 m/s, a continuación planteas la expresión del intervalo de tiempo correspondiente, y queda:
Δt = Δy/vLy ≅ 1000/2,485 ≅ 402,492 s ≅ 6 min 42,492 s,
y observa que la discrepancia entre ambos valores se debe a las aproximaciones que hemos realizado,
por lo que puedes concluir que la lancha tardaría aproximadamente 402,49 segundo en realizar el trayecto con aguas quietas.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/1/20a)
Has planteado y resuelto correctamente este inciso.
b)
Planteas la ecuación de continuidad (o de caudal) entre las secciones transversales correspondientes a los puntos A y B, y queda:
AA*vA = AB*vB, sustituyes las expresiones de las áreas de las secciones transversales, y queda:
π*rA2*vA = π*rB2*vB, divides por π y por rB2 en ambos miembros, y luego despejas:
vB = rA2*vA/rB2, reemplazas datos (observa que empleamos unidades internacionales), y queda:
vB = 0,052*2/0,042, resuelves, y queda:
vB = 3,125 m/s, que es la rapidez del líquido al pasar por la sección transversal correspondiente al punto B.
Luego, planteas la Ecuación de Bernoulli entre los puntos A y B (observa que ambos puntos se encuentran sobre el eje de simetría de la tubería, que es horizontal), y queda:
pA + (1/2)*δL*vA2 = pB + (1/2)*δL*vB2, restas (1/2)*δL*vB2 en ambos miembros, y luego despejas:
pB = pA + (1/2)*δL*vA2 - (1/2)*δL*vB2, extraes factores comunes entre los dos últimos términos, y queda:
pB = pA + (1/2)*δL*(vA2 - vB2), reemplazas datos y valores que ya tienes calculados, y queda:
pB = 111100 + (1/2)*1000*(22 - 3,1252), resuelves, y queda:
pB = 108217,1875 Pa, que es la presión del líquido en el punto B.
Luego, planteas la condición de equilibrio para un punto ubicado en la sección de la base del tubo vertical correspondiente al punto B, y queda:
pat + δL*g*hB = pB, restas x y luego divides por y en ambos miembros, y queda:
hB = (pB - pat)/(δL*g), reemplazas datos y valores que ya tienes calculados, y queda:
hB = (108217,1875 - 101300)/(1000*9,8), resuelves, y queda:
hB ≅ 0,706 m, que es el valor de la altura que alcanza el líquido en el tubo en estudio.
Espero haberte ayudado.
-
-
 No me queda claro si el radio debe ser la mitad, es decir 0,025 o 5... Porque me dice que debo aplicar las mismas condiciones. Ayuda y gracias!
No me queda claro si el radio debe ser la mitad, es decir 0,025 o 5... Porque me dice que debo aplicar las mismas condiciones. Ayuda y gracias!


Antonio Silvio Palmitano
el 7/1/20c)
Tienes dos cargas eléctricas puntuales qi = 0,8*10-6 C = 8*10-7 C, y qd = 0,8*10-6 C = 8*10-7 C.
Considera un sistema de referencia con eje OX sobre los puntos en los cuáles están ubicadas las cargas, con sentido positivo hacia la derecha según tu figura, y con origen de coordenadas en el punto medio entre las cargas, por lo que tienes que el punto en estudio es O(0,0).
Luego, observa que la carga de la izquierda está ubicada en el punto: A(-0,025;0) (en metros), y observa que la carga de la derecha está ubicada en el punto: B(0,025;0) (en metros).
Luego, planteas la expresión del vector posición del punto en estudio con respecto al punto A, y queda:
u = AO = < 0-(-0,025) ; 0-0 > = < 0,025 ; 0 > m, cuyo módulo es: |u| = 0,025 m = ri,
y cuyo vector unitario asociado es: U = u/|u| = < 1 ; 0 >;
luego, planteas la expresión vectorial del campo eléctrico producido por la carga eléctrica ubicada en el punto A, y queda:
Ei = (k*q1/ri2)*U = (9*109*8*10-7/0,0252)*< 1 ; 0 > = 1,152*107*< 1 ; 0 > = < 1,152*107 ; 0 > N/C (1).
Luego, planteas la expresión del vector posición del punto en estudio con respecto al punto B, y queda:
v = BO = < 0-0,025 ; 0-0 > = < -0,025 ; 0 > m, cuyo módulo es: |v| = 0,025 m = rd,
y cuyo vector unitario asociado es: V = v/|v| = < -1 ; 0 >;
luego, planteas la expresión vectorial del campo eléctrico producido por la carga eléctrica ubicada en el punto B, y queda:
Ed = (k*q2/rd2)*V = (9*109*8*10-7/0,0252)*< -1 ; 0 > = 1,152*107*< -1 ; 0 > = < -1,152*107 ; 0 > N/C (2).
Luego, planteas la expresión vectorial del campo eléctrico resultante en el punto en estudio, y queda:
EO = Ei + Ed, sustituyes las expresiones señaladas (1) (2), y queda:
EO = < 1,152*107 ; 0 > + < -1,152*107 ; 0 >, resuelves la suma vectorial (observa que los términos son opuestos), y queda:
EO = < 0 ; 0 >,
por lo que tienes que el campo eléctrico resultante en el punto en estudio es nulo.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 7/1/20Planteas la expresión de la energía mecánica inicial de la partícula cargada móvil, y queda:
EM1 = EC1 + EP1 = (1/2)*M*v12 + k*q1*q2/r1 (1).
Planteas la expresión de la energía mecánica final de la partícula cargada móvil (observa que la velocidad final es nula), y queda:
EM2 = EC2 + EP2 = (1/2)*M*v22 + k*q1*q2/r2 = (1/2)*M*02 + k*q1*q2/r2 = 0 + k*q1*q2/r2 = k*q1*q2/r2 (2).
Luego, como no están aplicadas fuerzas disipativas, planteas conservación de la energía mecánica, y queda la ecuación:
EM1 = EM2, sustituyes las expresiones señaladas (1) (2), y queda:
(1/2)*M*v12 + k*q1*q2/r1 = k*q1*q2/r2, divides por k en todos los términos, simplificas, y queda:
(1/2)*(M/k)*v12 + q1*q2/r1 = q1*q2/r2,
y aquí puedes continuar con el desarrollo que tienes en tu figura.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 7/1/20Recuerda que cuando tienes una ecuación, puedes multiplicar o dividir en todos los términos por un número distinto de cero.
Y es de aquí que en el desarrollo de tu figura el autor ha decidido dividir en todos los términos por k, que es una expresión distinta de cero.
Espero haberte ayudado.
-
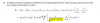
 Si me dice que el punto inicial es A por qué cuando llegamos al radio pone el final? Ayuda por favor, y muchísimas gracias!!
Si me dice que el punto inicial es A por qué cuando llegamos al radio pone el final? Ayuda por favor, y muchísimas gracias!!

Antonio Silvio Palmitano
el 7/1/20Observa que la distancia entre las cargas en la situación inicial es (observa que la primera carga se encuentra en el punto A):
ri = dist(A,B) = √([0-3]2 + [-4-0]2) = √(32 + 42) m.
Observa que la distancia entre las cargas en la situación final es (observa que la primera carga se encuentra en el origen de coordenadas):
rf = dist(O,B) = √([0-0]2 + [-4-0]2) = √(02 + 42) = √(42) = 4 m.
Espero haberte ayudado.
-

 Si tenemos en cuenta que es la componente y la que no se va, por qué pone coseno?? MUCHAS GRACIAS!!!!!!
Si tenemos en cuenta que es la componente y la que no se va, por qué pone coseno?? MUCHAS GRACIAS!!!!!!

Antonio Silvio Palmitano
el 7/1/20Además, observa que la dirección del campo eléctrico determina un ángulo de 45° con el eje OX, y también con el eje OY,
y si eliges el ángulo que determina la dirección del campo con el eje OY, entonces tienes que las expresiones de las componentes quedan:
Ex = E*sen(45°), Ey = E*cos(45°);
pero si eliges el ángulo que determina la dirección del campo con el eje OX, entonces tienes que las expresiones de las componentes quedan:
Ex = E*cos(45°), Ey = E*sen(45°).
En forma mnemotécnica:
si eliges el ángulo que determina el campo con un eje coordenado, entonces tienes que la componente según dicho eje queda expresada con el coseno del ángulo.
Espero haberte ayudado.
-
Un ejercicio:
Con una balanza se mide primero un vaso de precipitados vacío, lo cuál tiene como como resultado una masa de 62,7 g. Posteriormente se añaden 100 mL aproximadamente de agua y al pesar el conjunto tenemos 165,7 g. Se pesa un objeto de plástico dando como resultado 64,7g. Al pesar todo en la balanza, esta nos indica un valor de 230,4 g.
Se introduce ahora en la experiencia un dinamómetro. Al colgar en objeto de plástico en este, tenemos como resultado una masa de 65 g. Al introducir colgado el objeto del dinamómetro en el agua, el dinamómetro marca 30 g y la balanza indica 200,4 g.
Calcula el valor de la densidad del material del cilindro así como la densidad del agua.
-
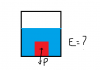
Hola, imagínense que tienen un cuerpo, el cual se sumerge en un vaso de precipitados el cual contiene agua. Al sumergirlo este va hacia el fondo, quedándose en contacto con la base del vaso. Se supondría que el empuje es nulo cuando el cuerpo está en esta situación?


Antonio Silvio Palmitano
el 7/1/20Debes tener que sobre un cuerpo que está parcial o totalmente sumergido, siempre está aplicado sobre él el empuje que ejerce el líquido.
En el caso de tu figura, observa que sobre el cuerpo están aplicadas tres fuerzas verticales, de las que indicamos sus módulos y sentidos (observa que el volumen de líquido desalojado es igual al volumen del cuerpo sumergido):
Peso: P = M*g, hacia abajo;
Acción normal de la base del vaso: N, hacia arriba;
Empuje del líquido: E = δL*Vc*g, hacia arriba.
Espero haberte ayudado.
-
Hola, una duda algo tonta sobre el funcionamiento del dinamómetro. Este se utiliza solo para medir el peso o también nos podía indicar la masa a modo de balanza?


Antonio Silvio Palmitano
el 7/1/20Observa que sobre un cuerpo colgado del dinamómetro están aplicadas dos fuerzas verticales, de las que indicamos sus módulos y sentidos:
Peso: P = M*g, hacia abajo,
Acción elástica del dinamómetro: Fe = k*Δs, hacia arriba;
luego, estableces un sistema de referencia con eje OY vertical con sentido positivo hacia arriba, aplicas la Primera Ley de Newton, y queda la ecuación:
Fe - P = 0, sumas P en ambos miembros, y queda:
Fe = P, sustituyes la expresión del módulo de la acción elástica del dinamómetro, y queda:
k*Δs = P, divides por k en ambos miembros, y queda:
Δs = P/k (1),
que es la expresión del estiramiento del dinamómetro, el cuál depende de su constante elástica, y del módulo del peso colgado.
Luego, sustituyes la expresión del módulo del peso del cuerpo colgado en la ecuación señalada (1), y queda:
Δs = M*g/k (2),
y observa que la expresión del estiramiento del dinamómetro señalada (2) depende de su constante elástica, de la masa del cuerpo colgado, y del módulo de la aceleración gravitatoria.
Luego, observa que no hemos obtenido una expresión que sea independiente del peso del cuerpo colgado, o del módulo de la aceleración gravitatoria, por lo que puedes concluir que el dinamómetro es útil para medir pesos, pero no es útil para medir masas, ya que es necesario conocer el valor del módulo de la aceleración gravitatoria terrestre en este último caso.
Espero haberte ayudado.

















