-
 preciso ayuda,lo que he intentado fue lo siguiente a) aplique la segunda ley de newton,con un sistema de referencia OX positivo hacia la derecha ya que el sistema se mueve hacia abajo y positivo en el eje OY,no estoy seguro de eso,preciso orientacion con respecto al SR. Al hacer eso llegue al sistema de ecuacion: T-PA=ma × a; pbx-T=mb x a . lo resolvi y llegue a que la aceleracion es -4m/s^2. Supongo que va frenando por que es negativa la aceleracion,si el SR hubiera sido al reves llegaba a la aceleracion positiva,esa es mi duda,saludos.
preciso ayuda,lo que he intentado fue lo siguiente a) aplique la segunda ley de newton,con un sistema de referencia OX positivo hacia la derecha ya que el sistema se mueve hacia abajo y positivo en el eje OY,no estoy seguro de eso,preciso orientacion con respecto al SR. Al hacer eso llegue al sistema de ecuacion: T-PA=ma × a; pbx-T=mb x a . lo resolvi y llegue a que la aceleracion es -4m/s^2. Supongo que va frenando por que es negativa la aceleracion,si el SR hubiera sido al reves llegaba a la aceleracion positiva,esa es mi duda,saludos.


Antonio Silvio Palmitano
el 14/2/20Vamos con los dos primeros incisos, el tercero queda para ti.
a)
Para el bloque colgante, considera un sistema de referencia con eje OY vertical con sentido positivo hacia arriba; luego, aplicas la Segunda Ley de Newton, y queda la ecuación (observa que sustituimos la expresión del módulo del peso del bloque):
T - MA*g = MA*a, y de aquí despejas: T = MA*g + MA*a (1).
Para el bloque deslizante, considera un sistema de referencia con eje OX paralelo a la rampa con sentido positivo hacia abajo, y con eje OY perpendicular a la rampa con sentido positivo hacia arriba; luego, aplicas la Segunda Ley de Newton, y quedan las ecuaciones (observa que sustituimos las expresiones de las componentes del peso del bloque):
MB*g*senθ - T = MB*a, de aquí despejas: T = MB*g*senθ - MB*a (2),
NB - MB*g*cosθ = 0, de aquí despejas: NB = MB*g*cosθ (3).
Luego, sustituyes la expresión señalada (1) en el primer miembro de la ecuación señalada (2), y queda:
MA*g + MA*a = MB*g*senθ - MB*a, de aquí despejas:
MA*a + MB*a = MB*g*senθ - MA*g, extraes factores comunes en ambos miembros, y queda:
(MA + MB)*a = (MB*senθ - MA)*g, divides por (MA + MB) en ambos miembros, y queda:
a = (MB*senθ - MA)*g/(MA + MB) (4).
Luego, reemplazas datos (MA = 60 Kg, MB = 40 Kg, θ = 30°, g = 10 m/s2), y queda:
a = (40*sen[30°] - 60)*10/(60 + 40), resuelves, y queda:
a = -4 m/s2,
por lo que tienes que para el bloque colgante la aceleración tiene el módulo cuyo valor hemos remarcado, con dirección vertical y sentido hacia abajo, y que para el bloque deslizante tienes que su aceleración tiene el valor que hemos remarcado, con dirección paralela a la rampa y sentido hacia arriba.
Luego, reemplazas valores en las ecuaciones señaladas (3) (1) (2), y queda:
NB = 40*10*cos(30°) ≅ 346,410 N,
T = 60*10 + 60*(-4) = 600 - 240 = 360 N,
T = 40*10*sen(30°) - 40*(-4) = 200 + 160 = 360 N,
por lo que tienes que el módulo de la acción normal que la rampa ejerce sobre el bloque deslizante es: NB ≅ 346,410 N,
y que el módulo de la tensión de la cuerda es: T = 360 N.
b)
Anulas los términos relacionados con el módulo de la tensión de la cuerda en las ecuaciones señaladas (1) (2), y queda:
0 =MA*g + MA*aA, y de aquí despejas: aA = -g,
0 = MB*g*senθ - MB*aB, y de aquí despejas: aB = g*senθ;
luego, reemplazas valores, resuelves, y queda:
aA = -10 m/s2, con dirección vertical y sentido hacia abajo
aB = 5 m/s2, con dirección paralela a la rampa y sentido hacia abajo.
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-


Breaking Vlad
el 12/2/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.


Antonio Silvio Palmitano
el 13/2/20Planteas la expresión del módulo de la componente tangencial de la aceleración, y queda:
aT = R*γ (1), y observa que es constante.
Luego, planteas la expresión del módulo de la velocidad angular, y queda:
ω = γ*t (2);
luego, planteas la expresión del módulo de la componente centrípeta de la aceleración, y queda:
acp = R*ω2, sustituyes la expresión señalada (2), distribuyes la potencia, y queda:
acp = R*γ2*t2 (3), y observa que es variable, ya que depende del tiempo.
Luego, vamos con las opciones de tu solucionario:
a)
Falsa, ya que a partir de la expresión señalada (1) tienes que el módulo de la componente tangencial de la aceleración es constante.
b)
Falsa, ya que a partir de la expresión señalada (3) tienes que el módulo de la componente centrípeta de la aceleración varía con el tiempo.
c)
Falsa, ya que la aceleración tiene componente tangencial que no es nula, y componente centrípeta que no es nula, por lo que tienes que la aceleración resultante no es perpendicular (ni paralela) a la velocidad lineal.
d)
Verdadera, ya que la componente tangencial de la aceleración es constante, pero la componente centrípeta aumenta con el tiempo, por lo que tienes que la componente de la aceleración que es perpendicular a la velocidad aumenta y, por lo tanto, también aumenta el ángulo determinado por los vectores velocidad y aceleración a medida que transcurre el tiempo.
e)
Falsa, por los motivos que hemos expuesto en la opción anterior.
f)
Falsa, porque la expresión señalada (2) es la expresión del módulo de la velocidad angular.
Espero haberte ayudado.
-
Hola, tengo un problema de campo magnético y no se hacer el último apartado. Los anteriores con la regla de la mano derecha y con F=qvB y F=mv^2/r y v=2*pi*r/T lo saco.
Un protón penetra en una zona donde existe un campo magnético uniforme de 8 T. La velocidad del protón es perpendicular a la dirección del campo magnético y de valor v = 3 · 10^7m/s.
a) Hacer un dibujo claro de los campos y fuerzas que actúan sobre el protón y de la trayectoria seguida
b) Calcular el radio de la órbita descrita.
c) Determinar el número de vueltas que da en 0,02 s.
d) ¿Cuál es el trabajo realizado por la fuerza magnética en el movimiento? Razonar la respuesta (0,5 puntos)
Datos: mprotón = 1,7 · 10^-27 kg qprotón = 1,6 · 10^-19 C
-
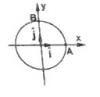
 lo que intente fue: T=8s; T=2pi/w ; wf=0,785rad/s,luego no estoy seguro,supongo, gamma=wf-w0/tf-t0, el tiempo final seria 5s , quedaria -0.157rad/s^2, por que esta frenando es negativo el signo?.supongo que como empieza a frenar en A,queda,. Pi=pi/2+0.785rad/s t +1/2 gamma t^2.preciso resolucion,desde ya gracias.
lo que intente fue: T=8s; T=2pi/w ; wf=0,785rad/s,luego no estoy seguro,supongo, gamma=wf-w0/tf-t0, el tiempo final seria 5s , quedaria -0.157rad/s^2, por que esta frenando es negativo el signo?.supongo que como empieza a frenar en A,queda,. Pi=pi/2+0.785rad/s t +1/2 gamma t^2.preciso resolucion,desde ya gracias.


Antonio Silvio Palmitano
el 13/2/20Tienes los datos del punto A, que son los iniciales para la etapa de frenado:
ti = 0 (instante inicial),
θi = π/2 rad (posición angular inicial),
ωi = 2π/T = 2π/8 = π/4 (velocidad angular inicial);
luego, planteas las ecuaciones de Movimiento Circular Uniformemente Variado, y queda:
θ = θi + ωi*t + (1/2)*α*t2,
ω = ωi + α*t,
reemplazas datos iniciales, y queda:
θ = π/2 + (π/4)*t + (1/2)*α*t2 (1),
ω = π/4 + α*t (2).
Luego, tienes las condición de detención: t = 5 s, ω = 0, reemplazas estos valores en la ecuación señalada (2), y luego despejas:
α = -π/20 rad/s2, que es el valor de la aceleración angular;
luego, reemplazas este último valor en las ecuaciones señaladas (1) (2), resuelves coeficientes, y queda:
θ = π/2 + (π/4)*t - (π/40)*t2 (1*),
ω = π/4 - (π/20)*t (2*).
a)
Tienes la posición del punto en estudio (B): θ = π rad, reemplazas este valor en la ecuación señalada (1*), y queda:
π = π/2 + (π/4)*t - (π/40)*t2, multiplicas por 40 y divides por π en todos los términos, y queda:
40 = 20 + 10*t - t2, sumas t2, restas 10*t y restas 20 en ambos miembros, y queda:
t2 - 10*t + 20 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
t = (5 + √[5]) s ≅ 7,236 s, que no tiene sentido para este problema (observa que el disco está detenido en este instante),
2°)
t = (5 - √[5]) s ≅ 2,764 s.
b)
Reemplazas el valor del instante en estudio que tienes remarcado en las ecuación señalada (2*), resuelves, y queda:
ωB ≅ 1,654 s;
luego, planteas la expresión de la velocidad lineal de un punto del borde del disco (cuyo radio tienes en tu enunciado), y queda:
vB = R*ωB ≅ 2*1,654 ≅ 3,308 m/s;
luego, planteas las expresiones de los módulos de las componentes tangencial y centrípeta de la aceleración en el punto B, y queda:
aT = R*|α| = 2*|-π/20| = π/10 m/s2 ≅ 0,314 m/s2,
acp = R*ωB2 ≅ 2*1,6542 ≅ 5,471 m/s2,
luego planteas la expresión del módulo de la aceleración del punto B, y queda:
aB = √(aT2 + acp2) ≅ √(0,3142 + 5,4712) ≅ √(30,030) ≅ 5,480 m/s2.
Espero haberte ayudado. -


Breaking Vlad
el 12/2/20Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.
-


Antonio Silvio Palmitano
el 11/2/20Consideramos que los datos iniciales son:
ti = 0, θi = 0, ωi = 0,
correspondientes a la momento en el cuál la marca se encuentra en la posición más baja.
Luego, planteas las ecuaciones de posición angular y de velocidad angular de Movimiento Circular Uniforme (consideramos positivo al giro antihorario), y queda:
θ = θi + ωi*(t - ti) + (1/2)*α*(t - ti)2,
ω = ωi + α*(t - ti),
reemplazas datos iniciales, cancelas términos nulos, y queda:
θ = (1/2)*α*t2 (1),
ω = α*t (2).
Luego, tienes la condición de referencia: t = 20 s, ω = 100 rad/s, reemplazas estos valores en la ecuación señalada (2), y queda:
100 = α*20, y de aquí despejas: α = 5 rad/s2, que es el valor de la aceleración angular de la marca;
luego, reemplazas este último valor remarcado en las ecuaciones señaladas (1) (2), resuelves coeficientes, y queda:
θ = (5/2)*t2 (1*),
ω = 5*t (2*).
Luego, observa que al llegar por primera vez al punto más alto, tienes que la posición angular es: θ = π rad, reemplazas este valor en la ecuación señalada (1*), y queda:
π = (5/2)*t2, y de aquí despejas:
t = √(2π/5) s ≅ 1,121 s, que es el valor del instante en el cuál la marca alcanza el punto más alto por primera vez;
luego, reemplazas este último valor remarcado en la ecuación señalada (2*), y queda:
ω = 5*√(2π/5) rad/s ≅ 5,605 rad/s, que es el valor de la velocidad angular de la marca.
Luego, planteas las expresiones de las componentes de la aceleración de la marca en el punto más alto, y queda:
aT = R*α = 10*5 = 50 m/s2 (módulo de la componente tangencial),
acp = R*ω2 = 10*[5*√(2π/5)]2= 100π m/s2 ≅ 314,159 m/s2 (módulo de la componente centrípeta),
por lo que puedes concluir que la opción señalada es la respuesta correcta.
Espero haberte ayudado.
-


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola, he resuelto el siguiente ejercicio, sin embargo hay una pequeña diferencia con la respuesta del libro:
Un vagón de mercancías de 75 Tm de peso es arrastrado por una fuerza constante de 500kp para subir un tramo de 1500m de longitud con una pendiente del 0,75%. Suponiendo que la velocidad inicial es de 15m/s y que la fuerza de rozamiento es de 4kp/Tm, calcular la velocidad al final del tramo.
El planteamiento de la ecuación balanceada es:
agradezco sus puntos de vista, en el libro sale 9.11 m/s...
Saludos Cordiales...
-
Hola, he resuelto el siguiente ejercicio, sin embargo hay una pequeña diferencia con la respuesta del libro:
Un vagón de mercancías de 75 Tm de peso es arrastrado por una fuerza constante de 500kp para subir un tramo de 1500m de longitud con una pendiente del 0,75%. Suponiendo que la velocidad inicial es de 15m/s y que la fuerza de rozamiento es de 4kp/Tm, calcular la velocidad al final del tramo.
El planteamiento de la ecuación balanceada es:
agradezco sus puntos de vista, en el libro sale 9.11 m/s...
Saludos Cordiales...