-
Buenas. Tenía una duda con respecto al apartado b) de este ejercicio.
Si me pueden decir si lo he hecho bien o no se lo agradecería, no sé si la sustitución del periodo es legal.
Y como apéndice, ¿podrían aclararme de dónde viene la conversión 1 eV - 1.6 x 10-19 J. Gracias máquinas.


Antonio Silvio Palmitano
el 3/12/19b)
Planteas la ecuación de Lorentz para la fuerza, aplicas la Segunda Ley de Newton, y queda la ecuación:
e*v*B = M*acp,
expresas el módulo de la aceleración centrípeta en función de la rapidez lienal y del radio orbital, y queda:
e*v*B = M*v2/R, divides por v en ambos miembros, y queda:
e*B = M*v/R, expresas a la rapidez lineal en función de la rapidez angular y del radio orbital, y queda:
e*B = M*ω*R/R, simplificas el segundo miembro, y queda:
e*B = M*ω, y de aquí despejas:
ω = e*B/M, expresas a la rapidez angular en función del periodo orbital, y queda:
2π/T = e*B/M, y de aquí despejas:
T = 2π*M/(e*B),
que es la expresión del periodo orbital del electrón en función de su masa, del valor absoluto de su carga, y del módulo del campo magnético, por lo que solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Usuario eliminado
el 3/12/19a)
Cuerpo A
Paralelamente al plano:
Fuerzas hacia arriba: componente paralela de la fuerza F (F·cos 37)
Fuerzas hacia abajo: componente paralela del peso de A (5·g·sen 37) y tensión T
Perpendicularmente al plano:
Fuerzas hacia arriba: reacción a la componente perpendicular de la fuerza F (F·sen 37) y reacción a la componente perpendicular del peso de A (5·g·cos 37)
Fuerzas hacia abajo: componente perpendicular de la fuerza F (F·sen 37) y componente perpendicular del peso de A (5·g·cos 37)
Cuerpo B
Paralelamente al plano:
Fuerzas hacia arriba: tensión T
Fuerzas hacia abajo: componente paralela del peso de B (3·g·sen 37)
Perpendicularmente al plano:
Fuerzas hacia arriba: reacción a la componente perpendicular del peso de B (3·g·cos 37)
Fuerzas hacia abajo: componente perpendicular del peso de B (3·g·cos 37)
Como no hay rozamiento, las fuerzas perpendiculares no nos interesan más que para dibujar el DCL
Sumando todas las fuerzas paralelas al plano obtendremos la resultante general paralela al plano obtendremos el valor de F (aprox. 85 N)
b)
En el instante en el que se rompe la cuerda, la velocidad de B vale
v = 0 + 2,5 · 6 = 15 m/s
Si en el instante t = 6 s se rompe la cuerda, el cuerpo B quedará sometido, en la dirección del plano, únicamente a la componente paralela de su peso, que está dirigida hacia abajo. Se moverá, pues, con un movimiento uniformemente acelerado, en el que el instante inicial t0 = 6 s, la velocidad inicial v0 = 15 m/s. La aceleración la encontramos sabiendo la resultante que actúa sobre B y su masa:
-3·g·sen 37 = 3 · a
de donde a = -6 m/s^2 (aprox.)
El signo - se debe a que se había tomado el sentido positivo hacia la parte superior del plano.
El cálculo de la velocidad para B a partir de t = 6 es fácil:
v7 = 15 - 6 · (7 - 6) = 9 m/s (velocidad positiva: sigue moviéndose hacia arriba)
v8 = 15 - 6 · (8 - 6) = 3 m/s (idem)
v9 = 15 - 6 · (9-6) = -3 m/s (entre el segundo 8 y el segundo 9 cambió de sentido: ahora se mueve hacia abajo)
v10 = 15 - 6 · (10 - 6) = -9 m/s
Para averiguar el instante en el que invierte el movimiento, hacemos v = 0:
0 = 15 - 6 · (t - 6)
t = 8,5 s
-


Antonio Silvio Palmitano
el 2/12/19Establece un sistema de referencia con origen de coordenadas en el muelle A, con eje de posiciones OX con dirección y sentido acordes a la corriente de agua (desde A hacia B), y con instante inicial (ti = 0) correspondiente al inicio de la etapa de nado desde A hacia B, y observa que empleamos este sistema de referencia en todas las etapas del problema.
a)
Tienes los datos de la primera etapa:
vc = 125 m/min (velocidad de la corriente con respecto a la tierra, que fluye con sentido desde A hacia B),
vn1 = +vn (a determinar, velocidad del nadador con respecto al agua, observa que es positiva),
t1i = 0 (instante inicial),
t1f = 4 min (instante final),
x1i = 0 (posición inicial en el tramo de ida),
x1f = 1,5 Km = 1500 m (posición final del tramo de ida);
luego, planteas la ecuación de posición de Movimiento Rectilíneo Uniforme, y queda la ecuación:
x = x1i + (vn1 + vc)*(t - t1i), reemplazas datos iniciales, cancelas términos nulos, y queda:
x = (vn1 + 125)*t;
luego, remplazas los datos finales, y queda:
1500 = (vn1 + 125)*4, divides por 4 en ambos miembros, y queda:
375 = vn1 + 125, restas 125 en ambos miembros, y luego despejas:
vn1 = 250 m/min, que es el módulo de la velocidad del nadador con respecto al agua.
Luego, tienes los datos de la segunda etapa:
vc = 125 m/min (velocidad de la corriente con respecto a la tierra, que fluye con sentido desde A hacia B),
vn2 = -250 m/min (velocidad del nadador con respecto al agua, observa que es negativa),
t2i = 4 min (instante inicial),
t2f = a determinar (instante final),
x21 = 1500 m (posición inicial en el tramo de vuelta),
x2f = 0 (posición final del tramo de vuelta);
luego, planteas la ecuación de posición de Movimiento Rectilíneo Uniforme, y queda la ecuación:
x = x2i + (vn2 + vc)*(t - t2i), reemplazas datos iniciales, y queda:
x = 1500 + (-250 + 125)*(t - 4);
luego, resuelves el coeficiente del último término, remplazas los datos finales, y queda:
0 = 1500 - 125*(t2f - 4), restas 1500 en ambos miembros, y queda:
-1500 = -125*(t2f - 4), divides por -125 en ambos miembros, y queda:
12 = t2f - 4, sumas 4 en ambos miembros, y luego despejas:
t2f = 16 min, que es el instante en el cuál el nadador llega al muelle A;
luego, planteas la expresión del intervalo de tiempo empleado en la segunda etapa, y queda:
Δt2 = t2f - t2i = 16 - 4 = 12 min.
b)
Ya tienes la ecuación de posición del nadador en su segunda etapa:
xn = 1500 - 125*(t - 4) (1);
luego, planteas la ecuación de posición de la nadadora (presta atención a los datos iniciales), y queda:
xN = 0 + (250 + 125)*(t - 4), cancelas el término nulo, resuelves el coeficiente en el último término, y queda:
xN = 375*(t - 4) (2).
Luego, planteas la condición de encuentro entre ambos nadadores, y quda:
xN = xn, sustituyes las expresiones señaladas (2) (1), y queda:
375*(t - 4) = 1500 - 125*(t - 4), sumas 125*(t - 4) en ambos miembros, y queda:
500*(t - 4) = 1500, divides por 500 en ambos miembros, y queda:
t - 4 = 3, sumas 4 en ambos miembros, y queda:
t = 7 min,
que es el instante en el cuál se encuentran los dos nadadores (observa que ambos llevan nadando tres minutos);
luego, reemplazas este último valor remarcado en las ecuaciones señalada (1) (2), resuelves, y queda
x = 1125 m,
que es la posición del punto de encuentro de los nadadores.
Espero haberte ayudado.
-
Buenos días, llevo varios días intentando realizar esto y no entiendo ¿Alguien me puede ayudar o hay algún vídeo que lo explique? Muchas gracias


Raúl RC
el 3/12/19Estás de suerte porque el profe grabó hace algún tiempo y como excepción varias vídeos tratando esta temática, espero puedan servirte ;)
https://www.unicoos.com/leccion/tecnologia/4-eso/electronica-digital/puertas-logicas
-
Usuario eliminado
el 1/12/19Si consideras que la presión hidrostática ha de ser la misma en el fondo del depósito de agua y en el punto al mismo nivel en el tubo, ya que el sistema está en equilibrio, tendrás
d(mercurio) · g · h(mercurio) = d(agua) · g · H(agua)
13500 · 9,8 · 0,100 = 1000 · 9,8 · H(agua)
H(agua) = 1,35 m
-


Antonio Silvio Palmitano
el 2/12/19Considera un sistema de referencia con origen de coordenadas en el último vagón del tren, con dirección y sentido positivo acordes al desplazamiento del tren.
Observa que la rapidez del hombre con respecto al tren es:
vh = 4*10/2 = 20 m/min.
Luego, tienes que la rapidez del tren con respecto a la tierra es:
vt = 54 Km/h = 54*1000/60 = 900 m/min.
a)
Planteas la expresión de la velocidad relativa del hombre con respecto al tren, y queda:
vh/t = -vh = -20 m/min (observa que el hombre se desplaza con sentido contrario al tren).
Planteas la expresión de la velocidad del hombre con respecto a la tierra, y queda:
vh/T = vh/t + vt = -20 + 900 = 880 m/min.
b)
Observa que el tren se desplaza con velocidad constante, por lo que consideramos un sistema de referencia firmemente unido al tren, con eje OX con dirección y sentido positivo desde el último vagón hacia el primero, con origen de coordenadas en el lado libre del último vagón, y con instante inicial: ti = 0 correspondiente al comienzo de los desplazamientos de los dos pasajeros que mencionan en tu enunciado.
Luego, tienes los datos iniciales para la señora: ti = 0, xi = 0, vs = 0,2 m/s = 0,2*(1/60) = 12 m/min,
planteas con ello la ecuación de posición de Movimiento Rectilíneo Uniforme, cancelas términos nulos, y queda:
xs = 12*t (1).
Luego, tienes los datos iniciales para el hombre: ti = 0, xi = 40 m, vh = -20 m/min,
planteas con ello la ecuación de posición de Movimiento Rectilíneo Uniforme, cancelas términos nulos, y queda:
xh = 40 - 20*t (2).
Luego, planteas la condición de encuentro, y queda la ecuación:
xs = xh, sustituyes las expresiones señaladas (1) (2), y queda:
12*t = 40 - 20*t, sumas 20*t en ambos miembros, y queda:
32*t = 40, divides por 32 en ambos miembros, y queda:
t = 1,25 min = 75 s;
luego, reemplazas este valor remarcado en las ecuaciones señaladas (19 (2), resuelves, y en ambas queda:
x = 15 m,
que es la posición del punto de encuentro entre los pasajeros.
Espero haberte ayudado.
-
Usuario eliminado
el 2/12/19Si se quiere que el bloque descienda con movimiento uniforme, la resultante de fuerzas paralelas al plano ha de ser nula. Para conseguir el movimiento uniforme, la fuerza ejercida sobre el bloque ha de estar dirigida hacia arriba; en caso contrario aumentaríamos su aceleración de bajada.
m·g·sen 45 - F(roz) - F = 0
De las fuerzas en el eje perpendicular averiguamos el valor de F(roz):
N - m·g·cos 45 = 0
N = m·g·cos 45
F(roz) = 0,1 · m·g·cos 45
Por tanto, en el eje paralelo al plano se cumplirá
m·g·sen 45 - 0,1·m·g·cos 45 - F = 0
de donde F = m·g·(sen 45 - 0,1·cos 45)
-
Buenas noches, ¿podrían decirme cómo se hace o se plantea este problema? Es que llevo toda la tarde con él y no lo consigo :)
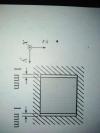
"Un bloque cúbico de 1m de lado está fabricado con un material homogéneo, isótropo y con comportamiento elástico lineal. Inicialmente se encuentra dentro de una cavidad rígida con huecos laterales de 1mm a cada lado en las direcciones x e y como se muestra en la figura; en la dirección del eje z , el bloque se encuentra perfectamente encajado pero sin sufrir tensiones. A continuación se calienta el cubo hasta que este toca las paredes laterales de la cavidad sin llegar sufrir tensiones normales en las direcciones x e y. En dichas condiciones, calcula:
a) Las deformaciones longitudinales unitarias en las direcciones de los ejes.
b) El incremento de temperatura del cubo.
c) Las tensiones normales en las direcciones de los ejes.
A continuación adjunto una foto el bloque:


Raúl RC
el 1/12/19Hola, lamento de corazón no poder ayudarte pero unicoos no trata dudas de física universitaria que no tengan que ver explícitamente con los vídeos ya grabados por el profe. Os recordamos que unicoos trata niveles de secundaria y bachiller y muy excepcionalmente universidad. Un saludo
-
si un camión va a 400 KM/H Y tarda 810 cuantos kilómetros tarda para llegar a su destino?


Breaking Vlad
el 29/11/19Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis siempre también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro.


Antonio Silvio Palmitano
el 29/11/19Vamos con una orientación.
Planteas la ecuación desplazamiento-velocidad-tiempo de Movimiento Rectilíneo Uniforme, y queda:
Δx = v*Δt,
y solo queda que reemplaces el valor de la rapidez del móvil, y del intervalo de tiempo correspondiente, éste último expresado en horas.
Espero haberte ayudado.
-
Hola únicos. La solución que da el libro es correcta? La aceleracion no sería F*cos30/m??? Muchas gracias



Antonio Silvio Palmitano
el 28/11/19Así es, pero observa los datos que tienes en tu enunciado (F = 20 N, M = 10 Kg, θ = 30°).
a = F*cos(30°)/M = 20*cos(30°)/10 = 2*cos(30°) = 2*√(3)/2 = √(3) m/s2 ≅ 1,732 m/s2,
por lo que tienes que la expresión de la aceleración que propones se corresponde con la respuesta que tienes consignada en tu libro.
Espero haberte ayudado.