-
 Hola,necesito la resolucion de este ejericicio.La barra homogeñea AB de peso 4kgf de la figura se encuentra en equilibrio vinculada a la pared mediante una articulacion fija en su extremo A, y por un cable tensor horizontal en su punto medio. En el extremo B cuelga una carga de igual peso que la barra .a) intensidad de la tensiom en el cable que vincula la barra con la pared. B) angulo que forma con la horizontal la fuerza que la articulacion le hace a la barra.
Hola,necesito la resolucion de este ejericicio.La barra homogeñea AB de peso 4kgf de la figura se encuentra en equilibrio vinculada a la pared mediante una articulacion fija en su extremo A, y por un cable tensor horizontal en su punto medio. En el extremo B cuelga una carga de igual peso que la barra .a) intensidad de la tensiom en el cable que vincula la barra con la pared. B) angulo que forma con la horizontal la fuerza que la articulacion le hace a la barra.

Francisco Javier
el 11/10/19Lo primero que debemos hacer es un diagrama de cuerpo libre donde se muestren todas las fuerzas presentes.
Te dejo un bosquejo de dicho diagrama al final de la respuesta.
Ahora, si hacemos una sumatoria de momentos en el punto A igual a cero (equilibrio) podemos hallar la tensión de cuerda.
Pero antes de esto, hay ciertas variables a definir y encontrar.
Recuerda que el momento de una fuerza se halla aplicando:
M = r*F
Donde "M" es el momento, "r" es la distancia perpendicular desde donde se aplica la fuerza al punto de estudio y "F" la fuerza.
El signo del momento sera positivo si este va en sentido anti-horario. De ir en sentido horario, su signo sera negativo.
Del diagrama podemos ver que las fuerzas que realizan momento en A son la tensión "T", el peso de la barra "wb" y el peso de la carga "wc".
Debemos averiguar ahora las distancias perpendiculares de cada una de estas fuerzas al punto A.
La distancia perpendicular entre "T" y el punto A la llamamos "h".
La distancia perpendicular entre "wb" y el punto A la llamamos "x1".
La distancia perpendicular entre "wc" y el punto B la llamamos "x2".
La determinación de estas distancias sale de la aplicación de trigonometría.
Para "h" nos concentramos en el triangulo ADE.
La función trigonométrica que nos relaciona el cateto adyacente (h) y la hipotenusa (L/2) es Cos(θ), donde θ = 53º.
Dicho esto:
Cos(53º) = h/(L/2)
Despejando "h":
h = (L/2)*Cos(53º)
Para "x1" nos concentramos en el triangulo AEF.
La función trigonométrica que nos relaciona el cateto opuesto (x1) y la hipotenusa (L/2) es Sin(θ), donde θ = 53º.
Dicho esto:
Sin(53º) = x1/(L/2)
Despejando "x1":
x1 = (L/2)*Sin(53º)
Para "x2" nos concentramos en el triangulo ABC.
La función trigonométrica que nos relaciona el cateto opuesto (x2) y la hipotenusa (L) es Sin(θ), donde θ = 53º.
Dicho esto:
Sin(53º) = x2/L
Despejando "x2":
x2 = L*Sin(53º)
Una vez hecho esto, podemos ahora si hacer la sumatoria de momentos en A:
∑MA = 0
T*h - wb*x1 - wc*x2 = 0
Reemplazando datos y despejando para "T":
T*(L/2)*Cos(53º) - 4*(L/2)*Sin(53º) - 4*L*Sin(53º) = 0
T*Cos(53º) - 4*Sin(53º) - 8*Sin(53º) = 0
T*Cos(53º) = 4*Sin(53º) + 8*Sin(53º)
T*Cos(53º) = 12*Sin(53º)
T = 12*[Sin(53º)/Cos(53º)] = 12*Tan(53º)
T ≈ 15.9 kgf
Haciendo una sumatoria de fuerzas en el eje vertical igual a cero (equilibrio) tenemos que:
∑Fy = 0
Ay - wb - wc = 0
Reemplazando datos y despejando para "Ay":
Ay - 4 - 4 = 0
Ay - 8 = 0
Ay = 8 kgf
Haciendo una sumatoria de fuerzas en el eje horizontal igual a cero (equilibrio) tenemos que:
∑Fx = 0
Ax - T = 0
Reemplazando datos y despejando para "Ax":
Ax - 12*Tan(53º) = 0
Ax = 12*Tan(53º) ≈ 15.9 kgf
Finalmente, el angulo que formara la fuerza de articulación A con la horizontal sera:
β = Tan-1(Ay/Ax) = Tan-1(8/[12*Tan(53º)])
β = 26.6736º
Bosquejo:
-
Buenos días,
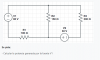
Estoy teniendo problemas con este ejercicio que hay que utilizar las leyes de Kirchoff, si alguien me pudiera explicar se lo agradecería.
¡Muchas gracias!
-
Buenas noches,
Tengo un problema con el siguiente ejercicio que no consigo resolverlo ¿Alguien podría ayudarme?
¡Muchas gracias!
Se supone que es utilizando las leyes de kirchhoff


Francisco Javier
el 10/10/19Asignamos con el nombre "I1" a la corriente que circulara por la malla izquierda en el sentido de las manecillas del reloj.
Asignamos con el nombre "I2" a la corriente que circulara por la malla derecha en el sentido de las manecillas del reloj.
Aplicaremos la ley de voltajes de kirchhoff la cual nos dice que la sumatoria de voltajes en una malla cerrada debe ser igual a cero.
∑V = 0
Para escribir las ecuaciones debemos hacer el recorrido asignado por la corriente en la malla.
Toda resistencia que nos encontremos a favor de la corriente tendrá una caída de voltaje positiva. De lo contrario, sera negativa.
Toda fuente de voltaje que nos encontremos tendrá el signo igual al borne donde llegue la corriente según el recorrido hecho.
Dicho esto, podemos empezar.
Para la malla izquierda (recorrido empezado antes de la fuente de 20 V en sentido horario):
20 + 4*(I1 - I2) - 10 + 2*I1 = 0
Para la malla derecha (recorrido empezado antes de la resistencia de 5 Ω en sentido horario):
5*I2 + 30 + 4*(I2 - I1) = 0
Ordenando un poco estas ecuaciones:
20 + 4*I1 - 4*I2 - 10 + 2*I1 = 0 → 6*I1 - 4*I2 = - 10
5*I2 + 30 + 4*I2 - 4*I1 = 0 → - 4*I1 + 9*I2 = - 30
Despejando "I1" de la primera ecuación:
6*I1 = 4*I2 - 10 → I1 = (4/6)*I2 - (10/6)
Reemplazando esto en la segunda ecuación:
- 4*[(4/6)*I2 - (10/6)] + 9*I2 = - 30
Y de aquí despejamos "I2":
- (8/3)*I2 + (20/3) + 9*I2 = - 30
- 8*I2 + 20 + 27*I2 = - 90
19*I2 = - 90 - 20
19*I2 = - 110
I2 = - (110/19) ≈ - 5.8 A
Por lo tanto la corriente "I1" valdrá:
6*I1 - 4*[- (110/19)] = - 10
6*I1 + (440/19) = - 10
114*I1 + 440 = - 190
114*I1 = - 190 - 440 = - 630
I1 = - (630/114) = - (105/19) ≈ - 5.5 A
El signo negativo en ambas corrientes indica que la corriente circula en sentido contrario al asumido.
Asignamos las corrientes que pasan por las resistencias para dar por concluido el problema:
IR1 = I1 = - (105/19) ≈ - 5.5 A
IR2 = I1 - I2 = - (105/19) - [- (110/19)] = (5/19) ≈ 0.26 A
IR3 = I2 = - (110/19) ≈ - 5.8 A
-
¿Pueden decirme alguna función de una sola variable que se utilice en física? Sin ser la de la Ley del enfriamiento de Newton, pero que también suceda cotidianamente digamos.


Antonio Silvio Palmitano
el 10/10/19Puedes pensar en un cuerpo cuya masa (M) es constante, que se encuentra acelerado (con aceleración: a), por acción de una fuerza resultante de todas las fuerzas que están aplicadas sobre él: F(a), aplicada sobre él. Luego, de acuerdo con la Segunda Ley de Newton, tienes que la expresión de la fuerza en función de la aceleración es:
F(a) = M*a,
donde la variable independiente es: a, y la variable dependiente es: F(a).
Espero haberte ayudado.

Clow
el 10/10/19Gracias por tu tiempo, no expliqué bien lo que necesitaba. Esa efectivamente es una función de una sola variable pero estoy buscando para un proyecto, y para darle contenido necesito alguna función más compleja, que dé para un estudio analítico más extenso y una representación gráfica más trabajada. Esa función no tiene máximos y mínimos y no da mucho juego jeje.
Gracias de todas maneras.


Antonio Silvio Palmitano
el 10/10/19Tal vez podría servirte el caso de un cañón, que dispara balas macizas y pesadas, con rapidez inicial 50 m/s, considerando qe el módulo de la aceleración gravitatoria terrestre es 9,8 m/s2.
Luego, planteas la expresión del alcance del arma en función de su ángulo de disparo con respecto a la horizontal, y queda:
A(θ) = vi2*sen(2*θ)/g, con valores del ángulo de disparo comprendidos entre 0 y π/2 radianes.
Espero haberte ayudado.
-
Si desde una altura de 200 metros sobre el suelo lanzas verticalmente y hacia arriba un objeto con una velocidad inicial de 30 m/s. Como calculas el tiempo que tarda a recorrer los ultimos 50m? Ayudaa plissss


Francisco Javier
el 10/10/19Planteamos la ecuación de posición del objeto, la cual tendrá la siguiente forma:
y = yo + vo*t - 0.5*g*t2
Donde "y" es la posición en cualquier tiempo, "yo" es la posición inicial, "vo" es la velocidad inicial, "t" el tiempo y "g" la gravedad.
Sabemos ya que:
g = 9.81 m/s2
Del problema:
vo = 30 m/s
Si tomamos como referencia el nivel del suelo:
yo = 200 m
Por lo tanto, nuestra ecuación de posición nos quedaría:
y = 200 + 30*t - 0.5*9.81*t2
Averiguamos que tiempo le toma al objeto llegar a estar a 50 m del piso aplicando la condición: y(t1) = 50
Dicho esto:
y(t1) = 200 + 30*t1 - 0.5*9.81*t12 = 50
De esta expresión despejamos para "t1":
200 + 30*t1 - 0.5*9.81*t12 - 50 = 0
- 4.905*t12 + 30*t1 + 150 = 0
Tenemos una ecuación cuadrática. Resolviéndola y omitiendo todo resultado negativo hallamos que:
t1 = 9.3774 s
Averiguamos que tiempo le toma al objeto llegar a estar a nivel de piso aplicando la condición: y(t2) = 0
Dicho esto:
y(t2) = 200 + 30*t2 - 0.5*9.81*t22 = 0
De esta expresión despejamos para "t2":
200 + 30*t2 - 0.5*9.81*t22 = 0
- 4.905*t22 + 30*t2 + 200 = 0
Tenemos una ecuación cuadrática. Resolviéndola y omitiendo todo resultado negativo hallamos que:
t2 = 10.1381 s
La diferencia entre estos dos tiempos sera el tiempo que demorara el objeto en caer los últimos 50 m, t3.
Dicho esto:
t3 = t2 - t1
t3 = 10.1381 - 9.3774
t3 = 0.7607 s
-
Hola,
Bueno, realmente podrían ayudarme con estos ejercicios? No me dan.
Gracias.
Ejercicio 1)
Ejercicio 2)
Ejercicio 3)
Ejercicio 4)


Antonio Silvio Palmitano
el 9/10/191)
Planteas la expresión de la energía mecánica inicial (observa que el bloque está en reposo, que el resorte está comprimido, y que consideramos que la energía potencial gravitatoria es igual a cero a nivel del punto más bajo del riel circular), y queda:
EMi = (1/2)*k*Δx2 (1).
Luego, plantea la expresión de la energía mecánica final, cuando el bloque se encuentra "apenas desprendido" del riel en su punto más elevado (observa que la energía potencial gravitatoria es distinta de cero, que la energía cinética de traslación es distinta de cero, y que el resorte está relajado), y queda:
EMf = M*g*(2*R) + (1/2)*M*vf2 = 2*M*g*R + (1/2)*M*vf2 (2);
y observa que la única fuerza que está aplicada sobre el bloque es su peso, por lo que aplicas la Segunda Ley de Newton, y tienes la ecuación:
M*g = M*acp, y de aquí despejas: acp = g (3);
luego, expresas al módulo de la aceleración centrípeta en función de la velocidad lineal del bloque y del radio de la trayectoria, y queda:
acp = vf2/R (4).
Luego, sustituyes la expresión señalada (4) en la ecuación señalada (3), y queda:
vf2/R = g, multiplicas por R en ambos miembros, y queda:
vf2 = g*R (5), y de aquí despejas:
vf = √(g*R), que es la expresión de la rapidez del bloque cuando se encuentra en el punto más alto del riel.
Luego, como tienes en tu enunciado que no se consideran los rozamientos, planteas conservación de la energía mecánica entre la situación inicial y la situación final, y queda la ecuación:
EMi = EMf, sustituyes las expresiones señaladas (1) (2), y queda:
(1/2)*k*Δx2 = 2*M*g*R + (1/2)*M*vf2, multiplicas por 2 en todos los términos, y queda:
k*Δx2 = 4*M*g*R + M*vf2, sustituyes la expresión señalada (5) en el último término, y queda:
k*Δx2 = 4*M*g*R + M*g*R, reduces términos semejantes en el segundo miembro, y queda:
k*Δx2 = 5*M*g*R, divides por k en ambos miembros, y queda:
Δx2 = 5*M*g*R/k, extraes raíz cuadrada positiva en ambos miembros, y queda:
Δx = √(5*M*g*R/k), que es la expresión de la compresión del resorte en la situación inicial.
Luego, solo queda que reemplaces datos expresados en unidades internacionales y hagas el cálculo.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 9/10/193)
Establece un sistema de referencia con eje OX horizontal con sentido positivo hacia la izquierda, y con eje OY vertical con sentido positivo hacia arriba.
Luego, planteas las expresiones de las componentes de la cantidad de movimiento inicial del sistema inmediatamente antes del choque (observa que la pelota está en movimiento y que la cuña está en reposo), y queda:
pix = Mp*v0 (1),
piy = 0 (2).
Luego, planteas las expresiones de las componentes de la cantidad de movimiento final del sistema inmediatamente después del choque (observa que la pelota y la cuña están en movimiento), y queda:
pfx = Mc*vc (3),
pfy = Mp*vf (4).
Luego, observa que la única fuerza exterior que está aplicada sobre el sistema pelota-cuña y no está equilibrada es el peso de la pelota, cuya dirección es vertical, por lo que tienes que la componente vertical de la cantidad de movimiento del sistema no se conserva, pero si se conserva la componente horizontal de la cantidad de movimiento, por lo que puedes plantear la ecuación:
pfx = pix, sustituyes las expresiones señaladas (3) (1), y queda:
Mc*vc = Mp*v0, divides por a en ambos miembros, y queda:
vc = Mp*v0/Mc,
que es la expresión de la rapidez de la cuña después del choque.
Luego, solo queda que reemplaces datos en la ecuación remarcada y hagas el cálculo.
Espero haberte ayudado.


Antonio Silvio Palmitano
el 9/10/194)
Planteas la expresión de la energía mecánica inicial (consideramos que la energía potencial gravitatoria es igual a cero a nivel del plano horizontal, y designamos con M1 a la masa total del primer esquiador más su equipo), y queda:
EMi = M1*g*hA (1).
Planteas la expresión de la energía mecánica cuando el primer esquiador alcanza el tramo horizontal antes del choque con el segundo esquiador, y queda:
EMa = (1/2)*M1*v1a2 (2).
Luego, planteas conservación de la energía mecánica entre estas dos situaciones, por lo que igualas las expresiones señaladas (2) (1), y queda la ecuación:
(1/2)*M1*v1a2 = M1*g*hA, aquí multiplicas por 2 y divides por M1 en ambos miembros, y queda:
v1a2 = 2*g*hA, extraes raíz cuadrada positiva en ambos miembros, y queda:
v1a = √(2*g*hA),
que es la expresión de la rapidez del primer esquiador antes del choque.
Luego, planteas las expresiones de la cantidad de movimiento antes y después del choque, y queda:
pa = M1*v1a (3),
pd = (M1+M2)*vd (4);
luego, como no actúan fuerzas exteriores en la dirección de movimiento, planteas conservación de la cantidad de movimiento, por lo que igualas las expresiones señaladas (4) (3), y queda la ecuación:
(M1+M2)*vd = M1*v1a, sustituyes la última expresión remarcada en el segundo miembro, y queda
(M1+M2)*vd = M1*√(2*g*hA), divides por (M1+M2) en ambos miembros, y queda:
vd = M1*√(2*g*hA)/(M1+M2),
que es la expresión de la rapidez del conjunto formado por los dos esquiadores y sus equipos inmediatamente después del choque.
Luego, planteas la expresión de la energía mecánica después del choque, y queda:
EMd = (1/2)*(M1+M2)*vd2, sustituyes la última expresión remarcada elevada al cuadrado, y queda:
EMd = (1/2)*(M1+M2)*M12*2*g*hA/(M1+M2)2, simplificas, y queda:
EMd = M12*g*hA/(M1+M2) (5).
Luego, planteas la expresión de la energía mecánica final, y queda:
EMf = (M1+M2)*g*hC (6).
Luego, planteas conservación de la energía entre las dos últimas situaciones, por lo que igualas las expresiones señaladas (6) (5), y queda la ecuación:
(M1+M2)*g*hC = M12*g*hA/(M1+M2), divides por g y divides por (M1+M2) en ambos miembros, y queda:
hC = M12*hA/(M1+M2)2,
que es la expresión de la altura máxima que alcanza el conjunto de los dos esquiadores con sus equipos.
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Hola,
Podrían ayudarme con este ejercicio por favor?
Una masa pequeña m=6kg está atada de una cuerda de longitud 6,2m cuyo extremo opuesto está fijo. Si la masa se suelta desde la posición horizontal con una velocidad 6,3m/s ¿Cuál es la tensión de la cuerda cuando llega a la posición vertical?
Gracias.


Antonio Silvio Palmitano
el 9/10/19Considera un sistema de referencia con origen en el punto más bajo que alcanza el objeto, con eje OY vertical con sentido positivo hacia arriba.
Luego, planteas la expresión de la energía mecánica inicial, y queda:
EMi = M*g*L + (1/2)*M*vi2 (1).
Luego, planteas la expresión de la energía mecánica final, y queda:
EMf = (1/2)*M*vf2 (2).
Luego, planteas conservación de la energía mecánica (observa que la tensión que ejerce la cuerda sobre el objeto es siempre perpendicular a su velocidad), por lo que igualas las expresiones señaladas (2) (1), y queda la ecuación:
(1/2)*M*vf2 = M*g*L + (1/2)*M*vi2, multiplicas por 2 y divides por M en todos los términos, y queda:
vf2 = 2*g*L + vi2 (3).
Luego, observa que cuando el objeto se encuentra en el punto más bajo de su trayectoria, tienes que sobre él están aplicadas dos fuerzas verticales: su peso (cuyo sentido es hacia abajo), y la tensión de la cuerda (cuyo sentido es hacia arriba), por lo que aplicas la Segunda Ley de Newton, y tienes la ecuación:
T - M*g = M*acp, aquí sumas M*g en ambos miembros, y quda:
T = M*g + M*acp;
luego, sustituyes la expresión del módulo de la aceleración centrípeta del objeto en función del radio de la trayectoria y de su rapidez lineal, y queda:
T = M*g + M*vf2/R, sustituyes la expresión señalada (3), y queda:
T = M*g + M*(2*g*L + vi2)/R, extraes factor común y denominador común, y queda:
T = M*(g*R + 2*g*L + vi2)/R,
que es la expresión del módulo de la tensión de la cuerda cuando el objeto se encuentra en el punto más bajo de su trayectoria.
Luego, solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-
Hola buenas tardes
Me prodrían ayudar con éstos ejercicios, es para explicárselos a mi hijo.
Muchas gracias.
1. Indica si las siguientes frases son correctas o erróneas y, en ese caso, escríbelas correctamente.
a) La sublimación es el paso directo de sólido a gas.
b) La licuefacción es el paso de gas a líquido.
c) El volumen de 1 kg de aire es el mismo cuando está frío que cuando está caliente.
d) La masa de 1 kg de aire es la misma cuando está frío que cuando está caliente.
2. Sobre tu mesa tienes dos esferas, una de hierro y la otra de madera. Ambas tienen 1 kg de masa.
a) ¿Tienen el mismo tamaño o una es mayor que la otra? En ese caso, ¿cuál es mayor?
b) ¿Cuál pesa más? ¿Cuál es más densa?
c) ¿Cuál haría subir más el nivel de agua si sumergimos cada una en una probeta?
3. De las siguientes propiedades, una no pertenece al mismo estado de agregación que las otras tres. ¿Cuál es? ¿De qué estado de agregación trata cada afirmación?
a) Ocupan todo el volumen del recipiente que los contiene.
b) No tiene forma fija.
c) Son poco compresibles.
d) Difunden o fluyen por sí mismos.
-
Hola buenas. ¿Podrían ayudarme con este ejercicio? Gracias.
El satélite Meteosat sigue una órbita geoestacionaria, es decir, gira en el plano ecuatorial a la misma velocidad angular que la Tierra.
a- ¿A qué distancia de la superficie terrestre está el Meteosat?
b- ¿Cuál es la energía cinética del Meteosat? ¿Cuál es la energía mínima que habría que proporcionarle para que se alejase indefinidamente de la Tierra?
c- ¿Qué energía hay que proporcionarle al Meteosat para ponerlo en órbita?


Antonio Silvio Palmitano
el 10/10/19Observa que la única fuerza que está aplicada sobre el satélite es la fuerza de atracción gravitatoria que la Tierra ejerce sobre él, cuyo módulo tiene la expresión:
F = G*MT*MS/(RT+h)2,
divides en ambos miembros por la masa del satélite, y la expresión del módulo de la aceleración centrítpeta del satélite queda expresado:
acp = G*MT/(RT+h)2 (1).
Luego, tienes que el satélite describe una órbita geoestacionaria, por lo que su rapidez angular es:
ω = 2π/24 rad/h = 2π/(24*3600) = π/43200 rad/s (2).
Luego, planteas la expresión del módulo de la aceleración centrípeta en función del radio orbital y de la rapidez angular, y queda:
acp = ω2*(RT+h) (3).
Luego, sustituyes la expresión señalada (3) en la ecuación señalada (1), y queda:
ω2*(RT+h) = G*MT/(RT+h)2, multiplicas por (RT+h)2 y divides por ω2 en ambos miembros, y queda:
(RT+h)3 = G*MT/ω2, extraes raíz cúbica en ambos miembros, y queda:
RT + h = ∛(G*MT/ω2), restas el valor del radio terrestre en ambos miembros, y queda:
h = ∛(G*MT/ω2) - RT,
que es la expresión de la altura orbital del satélite con respecto a la superficie de la Tierra, y solo queda que reemplaces el valor de la rapidez angular señalado (2), el valor de la constante de gravitación universal y el valor del radio terrestre, para luego hacer el cálculo.
Luego, planteas la expresión de la rapidez lineal del satélite en función del radio orbital y de la rapidez angular, y queda:
v = (RT+h)*ω (4).
Luego, planteas la expresión de la energía cinética de traslación del satélite, y queda:
EC1 = (1/2)*MS*v2, sustituyes la expresión señalada (4), resuelves el último factor, y queda:
EC1 = (1/2)*MS*(RT+h)2*ω2 (5),
y solo queda que reemplaces valores y hagas el cálculo.
Luego, planteas la expresión de la energía potencial gravitatoria del sistema Tierra-satélite, y queda:
EP1 = -G*MT*MS/(RT+h) (6).
Luego, planteas la expresión de la energía mecánica del satélite cuando se encuentra en órbita geoestacionaria, y queda:
EM1 = EC1 + EP1, sustituyes las expresiones señaladas (5) (6), y queda:
EM1 = (1/2)*MS*(RT+h)2*ω2 - G*MT*MS/(RT+h) (7).
Luego, si consideras que en la situación final tienes que el satélite se encuentra prácticamente en reposo, y muy alejado de la Tierra, entonces tienes que su energía potencial gravitatoria es prácticamente igual a cero, al igual que su energía cinética de traslación, por lo que la expresión de su energía mecánica final es:
EM2 = 0 (8).
Luego, puedes designar con ΔE a la energía adicional que se le da al satélite para poder trasladarlo hasta su posición final, planteas conservación de la energía mecánica, y queda la ecuación:
EM1 + ΔE = EM2, restas a en ambos miembros, y queda:
ΔE = EM2 - EM1, sustituyes las expresiones señaldas (8) (7), y queda:
ΔE = 0 - ( (1/2)*MS*(RT+h)2*ω2 - G*MT*MS/(RT+h) ),
cancelas el término nulo, distribuyes el signo en el último término, y queda:
ΔE = -(1/2)*MS*(RT+h)2*ω2 + G*MT*MS/(RT+h).
Luego, planteas la expresión de la energía mecánica total del satélite cuando se encuentra en la superficie terrestre a punto de ser lanzado (observa que que encuentra en reposo), y queda:
EMs = ECs + EPs = ECs - G*MT*MS/RT (9).
Luego, planteas conservación de la energía mecánica entre el lanzamiento del satélite y su llegada a la órbita geoestacionaria, y queda la ecuación:
EMs = EM1, sustituyes las expresiones señaladas (9) (7), y queda:
ECs - G*MT*MS/RT = (1/2)*MS*(RT+h)2*ω2 - G*MT*MS/(RT+h), sumas G*MT*MS/RT en ambos miembros, y queda:
ECs = (1/2)*MS*(RT+h)2*ω2 - G*MT*MS/(RT+h) + G*MT*MS/RT,
extraes factores comunes entre los dos últimos términos, y queda:
ECs = (1/2)*MS*(RT+h)2*ω2 + G*MT*MS*(-1/(RT+h) + 1/RT),
que es la expresión de la energía cinética de traslación que hay que suministrarle al satélite para poder trasladarlo desde la superficie terrestre hasta su órbita geoestacionaria, y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.