-
 hola me podrian ayudar con este ejercicio por favor. Es de solido rigido y me pide averiguar aceleracion del bloque
hola me podrian ayudar con este ejercicio por favor. Es de solido rigido y me pide averiguar aceleracion del bloque

Raúl RC
el 4/11/19Perdona por la tardanza Luz. Decirte que lamento no poder ayudarte con este ejercicio pues se sale del nivel general de unicoos (secundaria y bachiller).
Como excepción el profe ya grabó unos vídeos relacionados con momento de inercia que te sugiero que veas por si te pueden servir, lo lamento
Momento de inercia -


Antonio Silvio Palmitano
el 14/10/19Planteas las expresiones vectoriales de las fuerzas resultantes de los dos sistemas (te dejo el planteo), y queda:
Fα = < 1 , 3 , -2 >,
Fβ = < 1 , b , a+6 >;
luego, igualas componentes a componente, y de allí tienes: b = 3, a = -8.
Luego, planteas las expresiones vectoriales de los momentos de fuerza resultantes con respecto al origen de coordenadas (observa que reemplazamos los valores de las indeterminadas a y b en las expresiones vectoriales de las fuerzas), y queda:
τα = < 1 , 1 , -1 >x< 2 , 3 , -1 > + < 0 , 5 , 1 >x< 4 , -1 , 2 > + < 2 , -3 , 0 >x< 3 , -4 , 0 > + < 4 , 0 , -1 >x< -5 , 1 , -3 > + < 3 , -6 , 0 >x< -3 , 4 , 0 >,
resuelves los productos vectoriales en los términos, y queda:
τα = < 2 , -1 , 1 > + < 11 , 4 , -20 > + < 0 , 0 , 1 > + < 1 , 17 , 4 > + < 0 , 0 , - 6 >,
resuelves la suma vectorial, y queda:
τα = < 14 , 20 , -20 >;
τβ = < 0 , 0 , 0 >x< 3 , -2 , -8 > + < 6 , 0 , 2 >x< 2 , 3 , 4 > + < 3 , c , -10 >x< -4 , 2 , 0 >,
resuelves los productos vectoriales en los términos, y queda:
τβ = < 0 , 0 , 0 > + < -6 , -20 , 18 > + < 20 , 40 , 6+4c >,
resuelves la suma vectorial, y queda:
τβ = < 14 , 20 , 24+4c >;
luego, planteas la igualdad entre los momentos resultantes, igualas componente a componente, y tienes la ecuación:
24 + 4c = -20, y de aquí despejas:
c = -11.
Espero haberte ayudado.
-
Hola FRANCISCO JAVIER, POR FAVOR necesito la resolucion de este ejercicio un bloque cubico y macizo y homogeñeo de 0.5 m de arista y 600km/m3 de densidad se encuentra en equilibrio totalmente sumergido en agua contenida en un recipiente,vinculado al fondo del mismo por medio de una soga ideal que mantiene tensa y vertical. A) calcule la intensidad de la tension en la soga. B) explique que ocurrira con el bloque si se cortara la soga y determine la presion hidrostatica sobre la cara inferior del bloque cuando se encuentra nuevamente en equilibrio.
-
Si una partícula con masa m1 y velocidad v1 que viaja sobre el eje de las x choca contra un objeto con masa m2 y velocidad v2 sobre el mismo eje. Encuentre la velocidad final u1 y u2 en términos de v1 y v2. Suponga que el choque es completamente elástico por lo que la energía y el momento de todo el sistema se conserva. Por favor ayudenme


Francisco Javier
el 14/10/19Supongo que el choque se da frontalmente (unidimensional) y que la segunda masa tiene sentido contrario a la primera.
Planteamos la conservación de la cantidad de movimiento:
m1*v1 + m2*v2 = m1*u1 + m2*u2 [1]
Planteamos la conservación de la energía cinética:
0.5*m1*v12 + 0.5*m2*v22 = 0.5*m1*u12 + 0.5*m2*u22 [2]
De esta ultima ecuación, multiplicamos todo por "0.5" y acomodamos en cada miembro las "m1" y "m2":
m1*v12 + m2*v22 = m1*u12 + m2*u22
m1*v12 - m1*u12 = m2*u22 - m2*v22
m1*(v12 - u12) = m2*(u22 - v22)
Aplicando diferencia de cuadrados (factorización):
m1*(v1 - u1)*(v1 + u1) = m2*(u2 - v2)*(u2 + v2) [3]
Podemos arreglar la ecuación [1] de tal manera que nos quede:
m1*v1 + m2*v2 = m1*u1 + m2*u2
m1*v1 - m1*u1 = m2*u2 - m2*v2
m1*(v1 - u1) = m2*(u2 - v2) [4]
Dividiendo ahora la ecuación [3] entre la ecuación [4] nos quedaría:
v1 + u1 = u2 + v2 [5]
Despejando para "u2":
u2 = v1 + u1 - v2 [6]
Reemplazando la ecuación [6] en la ecuación [1]:
m1*v1 + m2*v2 = m1*u1 + m2*(v1 + u1 - v2)
Y trabajando esta ecuación podemos hallar "u1" en función de "v1" y "v2".
Veamos:
m1*v1 + m2*v2 = m1*u1 + m2*v1 + m2*u1 - m2*v2
m1*u1 + m2*u1 = m1*v1 + m2*v2 - m2*v1 + m2*v2
u1*(m1 + m2) = v1*(m1 - m2) + 2*m2*v2
u1 = [(m1 - m2)/(m1 + m2)]*v1 + [(2*m2)/(m1 + m2)]*v2
Reemplazando esta velocidad hallada en la ecuación [5]:
v1 + u1 = u2 + v2
u2 = v1 + u1 - v2
u2 = v1 + [(m1 - m2)/(m1 + m2)]*v1 + [(2*m2)/(m1 + m2)]*v2 - v2
Y trabajando esta ecuación podemos hallar "u2" en función de "v1" y "v2".
Veamos:
u2 = v1*{1 + [(m1 - m2)/(m1 + m2)]} + v2*{[(2*m2)/(m1 + m2)] - 1}
u2 = v1*[(2*m1)/(m1 + m2)] + v2*[(m2 - m1)/(m1 + m2)]
u2 = [(2*m1)/(m1 + m2)]*v1 + [(m2 - m1)/(m1 + m2)]*v2
Y con esto damos por concluido el problema.
-
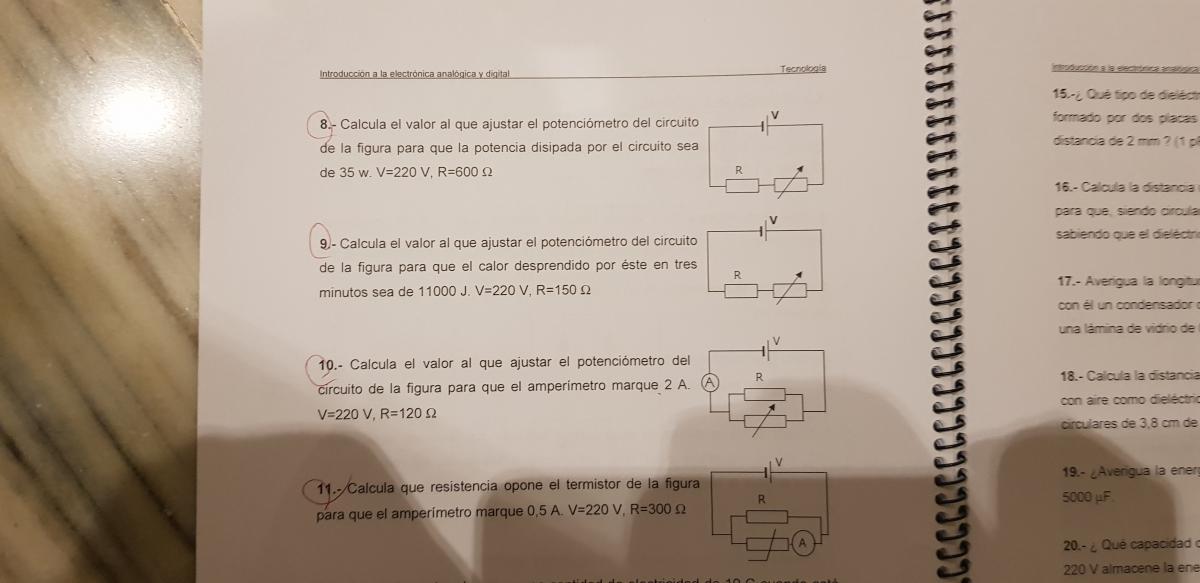 Buenas alguien me puede ayudar ha hacer estos ejercicios
Buenas alguien me puede ayudar ha hacer estos ejercicios


Francisco Javier
el 14/10/198.
La potencia total que disipa el circuito se puede hallar aplicando la siguiente ecuación:
PT = V*I
Donde "PT" es la potencia disipada, "V" es el voltaje de la fuente y "I" es la corriente que entrega la fuente.
De esta ecuación, despejando para "I":
I = PT/V
Y reemplazando datos del enunciado del problema:
I = 35/220
I = 7/44 ≈ 0.16 A
Debido a que el circuito es uno tipo serie, la corriente que entrega la fuente sera la misma corriente que pasara por las dos resistencias.
Osea:
I = IR = Ipotenciometro
Entonces, escribiendo la ecuación de malla (ley de voltajes de kirchhoff):
Rpotenciometro*Ipotenciometro + R*IR - V = 0
Rpotenciometro*I + R*I - V = 0
Finalmente, despejando para "Rpotenciometro" y reemplazando datos:
Rpotenciometro*I = V - R*I
Rpotenciometro = (V - R*I)/I
Rpotenciometro = [220 - 600*(7/44)]/(7/44)
Rpotenciometro = 5480/7 ≈ 782.9 Ω


Francisco Javier
el 14/10/199.
Interpreto que el dato de calor disipado se da para el potenciometro y no para el circuito.
El enunciado no lo deja muy claro, por lo que ya queda a cuestión de interpretación.
Si el dato se refiere al calor disipado por el circuito, el problema se hace mas fácil.
Te lo puedo desarrollar también si asi lo indicas.
Dicho esto, te dejo la resolución con la primera interpretación.
La energía total que disipa el potenciometro se puede hallar aplicando la siguiente ecuación:
ET = Rpotenciometro*Ipotenciometro2*t
Donde "ET" es la energía total disipada (calor) por el potenciometro y "t" el tiempo.
"R" e "I" representan la resistencia y la corriente del potenciometro respectivamente.
Si escribimos la ecuación de malla (ley de voltajes de kirchhoff):
Rpotenciometro*Ipotenciometro + R*IR - V = 0
Donde "IR" es la corriente de la resistencia "R".
Como se trata de un circuito en serie, la corriente es la misma en todas partes.
Quiere decir que:
Ipotenciometro = IR = I
Entonces:
ET = Rpotenciometro*I2*t
Y:
Rpotenciometro*I + R*I - V = 0
Despejando para "I":
Rpotenciometro*I + R*I = V
I*(Rpotenciometro + R) = V
I = V/(Rpotenciometro + R)
Reemplazando esta corriente en la ecuación de energía total disipada:
ET = Rpotenciometro*I2*t
ET = Rpotenciometro*[V/(Rpotenciometro + R)]2*t
Ahora reemplazamos los datos que da el problema. Pasamos el tiempo a unidad acorde al sistema internacional de medidas (SI).
t = 3 min*(60 s /1 min) = 180 s
Entonces:
11000 = Rpotenciometro*[220/(Rpotenciometro + 150)]2*180
11000 = Rpotenciometro*[8712000/(Rpotenciometro + 150)2]
Esta ecuación debe ser trabajada algebraicamente para despejar "Rpotenciometro".
Te dejo dicha tarea.
Cuando logres hacer dicho despeje, llegaremos a que:
Rpotenciometro = 51.0231 Ω ó 440.9770 Ω
Puedes ajustar a cualquiera de estos dos valores el potenciometro para lograr lo establecido.


Francisco Javier
el 14/10/1910.
Las resistencias "R" y "Rpotenciometro" están en paralelo con la fuente de voltaje "V".
Quiere decir que ambas resistencias van a tener el mismo voltaje de la fuente:
VR = Vpotenciometro = V
Aplicando ley de ohm podemos hallar el valor de la corriente que pasa por la resistencia "R".
Recordamos que la ley de ohm se expresa como:
VR = IR*R
V = IR*R
Entonces, despejando para "IR":
IR = V/R
Y reemplazando datos del problema:
IR = 220/120 = 11/6 ≈ 1.83 A
Ahora, aplicando la ley de corrientes de kirchhoff al nodo del lado del amperimetro tenemos que:
IA = IR + Ipotenciometro
Donde "IA" es la corriente del amperimetro. Despejando para "Ipotenciometro":
Ipotenciometro = IA - IR
Y reemplazando datos:
Ipotenciometro = 2 - 11/6
Ipotenciometro = 1/6 ≈ 0.17 A
Finalmente, aplicando nuevamente ley de ohm ahora al potenciometro:
Vpotenciometro = Ipotenciometro*Rpotenciometro
V= Ipotenciometro*Rpotenciometro
Despejando y reemplazando datos para "Rpotenciometro":
Rpotenciometro = V/Ipotenciometro
Rpotenciometro = 220/(1/6)
Rpotenciometro = 1320 Ω


Francisco Javier
el 14/10/1911.
Escribiendo la ecuación de malla externa (sin pasar por la resistencia "R") tenemos que:
Rtermistor*IA - V = 0
Donde "IA" es la corriente del amperimetro y "V" el voltaje de la fuente.
Despejando para "Rtermistor":
Rtermistor*IA = V
Rtermistor = V/IA
Y reemplazando datos damos con la respuesta:
Rtermistor = 220/0.5
Rtermistor = 440 Ω
Como puedes ver, el valor de esta resistencia es independiente del valor que tome "R".
-
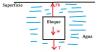
Hola necesito la resolucion de este ejercicio un bloque cubico y macizo y homogeñeo de 0.5 m de arista y 600km/m3 de densidad se encuentra en equilibrio totalmente sumergido en agua contenida en un recipiente,vinculado al fondo del mismo por medio de una soga ideal que mantiene tensa y vertical. A) calcule la intensidad de la tension en la soga. B) explique que ocurrira con el bloque si se cortara la soga y determine la presion hidrostatica sobre la cara inferior del bloque cuando se encuentra nuevamente en equilibrio.


Francisco Javier
el 14/10/19Hacemos un diagrama de cuerpo libre de la situación.
Te dejo un bosquejo de dicho diagrama al final de la respuesta.
Como puedes observar, hay presencia de tres fuerzas.
"Fb" es la fuerza de flotación, "T" es la tensión de cuerda y "w" el peso del cubo.
La fuerza de flotación se encuentra aplicando la siguiente ecuación:
Fb = γf*Vd
Donde "γf" es el peso especifico del fluido y "Vd" es el volumen desplazado o sumergido.
Esta siempre va dirigida en el eje de tal forma de hacer que el objeto flote.
El peso se encuentra aplicando la siguiente ecuación:
w = γ*V
Donde "γ" es el peso especifico del objeto y "V" su volumen.
Recordemos que el peso especifico se halla aplicando la ecuación.
γ = ρ*g
Donde "ρ" es la densidad y "g" la gravedad.
Adaptando estas ecuaciones a nuestra situación:
γagua = ρagua*g
γbloque = ρbloque*g
Donde para el agua usaremos:
ρagua = 1000 kg/m3
Y evidentemente:
g = 9.81 m/s2
Para el volumen desplazado, fíjate que el bloque esta totalmente sumergido.
Quiere decir que el volumen desplazado es igual al volumen del bloque. Matemáticamente:
Vd = Vbloque
Y al tratarse de un cubo:
Vbloque = a3 = 0.53
Donde "a" es la longitud de los lados.
Una vez aclarado todo esto, nuestras ecuaciones de fuerza de flotación y peso nos quedarían de la siguiente forma respectivamente:
Fb = γfluido*Vd = γagua*Vbloque = ρagua*g*Vbloque
w = γbloque*Vbloque = ρbloque*g*Vbloque
Ahora, haciendo una sumatoria de fuerzas verticales igual a cero (equilibrio) tenemos que:
Fb - w - T = 0
ρagua*g*Vbloque - ρbloque*g*Vbloque - T = 0
Suponiendo que lo dirigido hacia arriba es positivo y lo dirigido hacia abajo negativo.
Despejando para "T":
T = ρagua*g*Vbloque - ρbloque*g*Vbloque
Y reemplazando datos:
T = 1000*9.81*0.53 - 600*9.81*0.53
T = 490.5 N
La presión se define como la fuerza aplicada entre el área que perturba. Matemáticamente:
P = F/A
Dicha área seria:
A = a2 = 0.52
Y la fuerza aplicada en este punto es la de tensión ya encontrada.
Reemplazamos valores para terminar con el problema:
P = F/A = 490.5/0.52
P = 1962 Pa
Bosquejo:
-
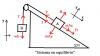
Hola.por favor necesito la resolucion de este ejercicio.Los bloques A y B de la figura cuyas masas ma=10kg y mb=5 kg,estan vinculadas por medio de una soga ideal que pasa por una polea fija (tambien ideal).el bloque A se encuentra apoyado sobre el plano inclinado con rozamiento (ue=0,6 ; ud=0,4).ligado a un resorte ideal de constante elastica k=232 N/m,fijo en su parte inferior. A) halle la maxima compresion que puede darse al resorte (respecto desu longitud natural) para mantener el sistema en equilibrio. B) si se comprime al resorte 40 cm respecto de su longitud natural y se libera el sistema a partir del reposo calcule la intensidad de la fuerza de rozamiento que actuara sobre el bloque A un instante inmediatamente despues de dejar el sistema en libertad.indicando claramente su sentido



Francisco Javier
el 14/10/19Hacemos un diagrama de cuerpo libre del problema.
Dicho diagrama te lo dejo al final de la respuesta.
Como puedes ver del diagrama, sobre el bloque A actúan múltiples fuerzas.
En el eje paralelo al plano están la tensión "T", la componente del peso en dicho eje "wAx", la fricción "ƒ" y la fuerza del resorte "Fr".
En el eje perpendicular al plano actúan la normal "N" y la componente del peso en dicho eje "wAy".
Para el bloque B actúan menos fuerzas. Esta la misma tensión "T" y el peso "wB". Ambas en el eje vertical.
Las componentes del peso del bloque A son determinadas de la descomposición en componentes rectangulares.
Para un plano inclinado con angulo de inclinación "θ" respecto al suelo, siempre se cumple que:
wx = w*Sin(θ)
wy = w*Cos(θ)
Y como el peso se define como:
w = m*g
Donde evidentemente:
g = 9.81 m/s2
Quedaría:
wx = m*g*Sin(θ)
wy = m*g*Cos(θ)
Adaptando a nuestras variables:
wAx = mA*g*Sin(θ)
wBy = mA*g*Cos(θ)
Para la masa B:
wB = mB*g
La fuerza de fricción "ƒ" se halla aplicando la siguiente ecuación:
ƒ = μ*N
Donde "μ" es el coeficiente de fricción y "N" es la fuerza normal.
El coeficiente de fricción puede ser estático "μs" o dinámico "μk".
Cuando se esta el sistema en equilibrio se usa el estático y cuando hay movimiento se usa el dinámico.
Quiere decir que para la primera incógnita, debemos usar le coeficiente de fricción estático.
Por lo que la ecuación de fricción a utilizar debe ser:
ƒ = μs*N
La fuerza del resorte "Fr" se halla aplicando la siguiente ecuación:
Fr = - k*x
Donde "k" es la constante de rigidez del resorte y "x" es la posición del resorte respecto a su posición original.
El signo negativo indica que la fuerza del resorte siempre es opuesta al movimiento.
Para este problema, la compresión del resorte indicara un valor de "x" negativo. De lo contrario, "x" sera positivo.
Una vez dicho todo esto, empezamos a desarrollar. Importante obedecer el sistema de referencia asignado en el bosquejo.
Empezamos haciendo una sumatoria de fuerzas en el eje vertical para el bloque B igual a cero (equilibrio).
De esta expresión se encontrara la tensión "T".
Dicho esto:
∑Fy = 0
T - wB = 0
Despejando para "T" y reemplazando datos:
T = wB
T = mB*g
T = 5*9.81
T = 49.05 N
Hacemos lo mismo para el bloque A.
Sumatoria de fuerzas perpendiculares al plano igual a cero (equilibrio):
∑Fy = 0
N - wAy = 0
Despejando para "N" y reemplazando datos:
N = wAy = mA*g*Cos(θ)
N = 10*9.81*Cos(37º)
N = 78.3461 N
Ahora, haciendo una sumatoria de fuerzas en el eje paralelo al plano para el bloque A igual a cero (equilibrio):
∑Fx = 0
wAx + Fr - ƒ - T = 0
Reemplazamos las expresiones correspondientes a la componente del peso, fricción y fuerza del resorte:
mA*g*Sin(θ) + (- k*x) - μs*N - T = 0
Despejando para "x":
k*x = mA*g*Sin(θ) - μs*N - T
x = [mA*g*Sin(θ) - μs*N - T]/k
Y reemplazando datos:
x = [10*9.81*Sin(37º) - 0.6*78.3461 - 49.05]/232
x = - 0.1596 m
Como ya mencionamos arriba, el signo negativo indica compresión del resorte.
Ahora, si comprimimos mas de este valor el resorte y luego soltamos el sistema, habrá movimiento. O al menos eso nos hace creer el enunciado.
Esto debemos demostrarlo. Veamos como.
El hecho de que haya movimiento modifica solo un poco el diagrama de cuerpo libre.
Ese poco es el sentido de la fuerza de fricción. Para cuando halla movimiento esta actuara en sentido contrario al señalado antes (+ x).
Entonces, tendremos ahora dos fuerzas en el eje (+ x): wAx y ƒ
Para el eje (- x) tendremos la fuerzas: T y Fr
Fíjate que en realidad"Fr" actúa en (- x) por el signo que su formula involucra y "ƒ" sigue usando el valor del coeficiente de fricción estático.
La suma de las fuerzas entre "T" y "Fr" debe ser mayor a la suma de las fuerzas entre "wAx" y "ƒ" para que haya movimiento.
T + Fr wAx + ƒ
T + (- k*x) > mA*g*Sin(θ) + μs*N
Pasamos el valor de "x" a unidad acorde al sistema internacional de medidas (SI):
x = 40 cm*(1 m/100 cm) = 0.4 m
Como esta en compresión:
x - 0.4 m
Reemplazando datos:
49.05 + (- 232*-0.4) > 10*9.81*Sin(37º) + 0.6*78.3461
141.85 > 106.046
Se cumple la condición, por lo que, ahora si, podemos garantizar que habrá movimiento.
Al haber movimiento, ya el coeficiente de fricción estático no se usa. Se pasa a utilizar el dinámico como ya mencionamos anteriormente.
Y como ya definimos la fuerza de fricción, esta aparte del coeficiente de fricción solo depende de la normal.
Y esta no cambia en la transición equilibrio-movimiento.
Por lo tanto, la fuerza de fricción justo después de soltar el resorte se halla aplicando la ecuación:
ƒ = μk*N
Reemplazando datos y desarrollando:
ƒ = 0.4*78.3461
ƒ = 31.3384 N
Y su dirección sera en el eje (+ x).
Bosquejo:
-


Antonio Silvio Palmitano
el 13/10/19Haz un esquema gráfico para visualizar mejor la situación.
Establece un eje de posiciones (alturas) OY vertical, con sentido positivo hacia arriba, y con origen de coordenadas en el punto más bajo que alcanza Tarzán al recorrer la trayectoria.
Luego, tienes los datos iniciales:
vi = 0 (rapidez lineal inicial, ya que tienes que Tarzán parte desde el reposo),
yi = L - L*cos(45°) = L*( 1 - cos(45°) ) (posición inicial);
luego, planteas la expresión de la energía mecánica inicial (observa que solo tienes energía potencial gravitatoria), y queda:
EMi = MT*g*yi = MT*g*yi = MT*g*L*( 1 - cos(45°) ) (1).
Luego, tienes los datos finales:
vf = a determinar (rapidez final),
yf = L - L*cos(30°) = L*( 1 - cos(30°) ) (posición final);
luego, planteas la expresión de la energía mecánica final, y queda:
EMf = MT*g*yf + (1/2)*MT*vf2 = MT*g*L*( 1 - cos(30°) ) + (1/2)*MT*vf2 (2).
Luego, planteas conservación de la energía mecánica (observa que se desprecia todo tipo de rozamiento), y queda la ecuación:
EMf = EMi, sustituyes las expresiones señaladas (2) (1), y queda:
MT*g*L*( 1 - cos(30°) ) + (1/2)*MT*vf2 = MT*g*L*( 1 - cos(45°) ), multiplicas por 2 y divides por MT en todos los términos, y queda:
2*g*L*( 1 - cos(30°) ) + vf2 = 2*g*L*( 1 - cos(45°) ), restas 2*g*L*( 1 - cos(30°) ) en ambos miembros, y queda:
vf2 = 2*g*L*( 1 - cos(45°) ) - 2*g*L*( 1 - cos(30°) ), distribuyes en el segundo miembro, cancelas términos opuestos, extraes factores comunes, y queda:
vf2 = 2*g*L*( -cos(45°) + cos(30°) ), extraes raíz cuadrada positiva en ambos miembros, y queda:
vf = √[2*g*L*( -cos(45°) + cos(30°) )],
y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
-


Francisco Javier
el 14/10/19Si se tratan de amplificadores operacional ideales, la caída de voltaje en sus terminales de entrada es nula por falta de corriente.
Por lo tanto, para el amplificador de la izquierda puedes decir que el voltaje en el nodo A y en el nodo B es igual. Matemáticamente:
VA = VB
Pero como "VB" esta conectado a tierra, su voltaje es cero.
Entonces:
VA = VB = 0
Para el amplificador de la derecha, el voltaje del nodo C es el mismo que en el nodo E. Matemáticamente:
VC = VE
Para facilitar el trabajo, hacemos transformación de fuente en las dos ramas antes del nodo A (fuentes de voltaje en serie con resistencias).
El valor de la fuente de corriente se determina aplicando ley de ohm:
I = V/R
El sentido de esta fuente de corriente sera como saliendo del borne positivo de la fuente de voltaje que se transformo.
La resistencia quedaría en paralelo con la respectiva fuente de corriente transformada.
Para la fuente de voltaje de 5 V en serie con 10 kΩ:
Ifuente = V/R = 5/10x103 = 1/2000 A
Esta fuente de corriente estará entrando al nodo A.
R = 10 kΩ
Para la fuente de voltaje de 10 V en serie con 5 kΩ:
Ifuente = V/R = 10/5x103 = 1/500 A
Esta fuente de corriente estará saliendo del nodo A.
R =5 kΩ
Aplicando ahora la ley de corrientes de Kirchhoff (corrientes que salen al nodo igual a las que salen) en el nodo A tenemos que:
(1/2000) + (VD/80 k) + (VC/40 k) = (1/500) + (VA/10 k) + (VA/5 k) + (VA/80 k) + (VA/40 k)
Como VA = 0:
(1/2000) + (VD/80 k) + (VC/40 k) = (1/500)
(VD/80 k) + (VC/40 k) = (1/500) - (1/2000)
(1/80000)*VD + (1/40000)*VC = 3/2000
Y como VC = VE:
(1/80000)*VD + (1/40000)*VE = 3/2000 [1]
Aplicando ahora la ley de corrientes de Kirchhoff en el nodo E tenemos que:
(VE/20 k) + (VE/ 40 k) = (VD/20 k)
(3/40000)*VE = (1/20000)*VD
Despejando para "VD":
VD = (3/2)*VE [2]
Reemplazando [2] en [1]:
(1/80000)*[(3/2)*VE] + (1/40000)*VE = 3/2000
Despejando para "VE" y desarrollando obtenemos que:
VE = 240/7 ≈ 34.3 V
Reemplazando este voltaje en la ecuación [1]:
(1/80000)*VD + (1/40000)*(240/7) = 3/2000
Despejando para "VD" y desarrollando obtenemos que:
VD = 360/7 ≈ 51.4 V
Por lo tanto, la corriente "I" valdrá:
I = VD/10 k = (360/7)/10 k
I = 9/1750 ≈ 5.1x10-3 A
Y finalmente, el voltaje "Vo" valdrá:
Vo = VE = 240/7 ≈ 34.3 V