-


Antonio Silvio Palmitano
el 1/10/19Vamos con una orientación.
Considera un sistema de referencia con eje OX horizontal con sentido positivo hacia la derecha, y con eje OY vertical con sentido positivo hacia arriba, según tu figura.
Luego, observa que las componentes de la velocidad antes del primer choque quedan expresadas:
v1x = v*cos(45°) = 2,5*√(2)/2 = 1,25*√(2) m/s,
v1y = v*cos(45°) = 2,5*√(2)/2 = 1,25*√(2) m/s.
Luego, observa que en el primer choque se conserva la componente horizontal (observa que es paralela a la banda), y tienes que se modifica la componente vertical, por lo que las componentes de la velocidad después del primer choque (y también antes del segundo choque) quedan expresadas:
v2x = 1,25*√(2) m/s,
v2y = -0,6*1,25*√(2) = -0,75*√(2) m/s.
Luego, observa que en el segundo choque se conserva la componente vertical (observa que es paralela a la banda), y tienes que se modifica la componente horizontal, por lo que las componentes de la velocidad después del segundo choque quedan expresadas:
v2x = -0,6*1,25*√(2) = -0,75*√(2) m/s,
v2y = -0,6*1,25*√(2) = -0,75*√(2) m/s.
Luego, con estas dos expresiones, puedes calcular el módulo de la velocidad después del segundo choque, y también el valor del ángulo que forma con la dirección horizontal.
Espero haberte ayudado.
-
Hola, tengo una pregunta: Hay un tipo de gráficas en las cuales la fórmula es: y=ax+b y me gustaría saber a qué se refiere la letra b. Un saludo.


Antonio Silvio Palmitano
el 30/9/19Tienes la ecuación de la gráfica de una función lineal:
f(x) = a*x + b,
y observa que si la evalúas para x = 0, entonces tienes:
f(0) = a*0 + b = 0 + b = b,
por lo que tienes que el punto: B(0,b) pertenece a la gráfica, y observa que también pertenece al eje coordenado OY,
por lo que tienes que el valor b te indica el valor de la ordenada en el cuál la gráfica de la función corta a dicho eje.
Espero haberte ayudado.
-
Buenas tardes.
me podrian decir si esto esta bien planteado
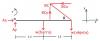
Un automóvil sale de Barcelona a las 6 de la tarde con una aceleración de 10 m/s2, y una moto sale a la misma hora de Zaragoza con una velocidad de 100 m/s. Ambas ciudades distan 350 km. Calcula:
 a) En qué punto se encontrarán el automóvil y la moto.
a) En qué punto se encontrarán el automóvil y la moto.b) A qué hora se encontrarán.


Antonio Silvio Palmitano
el 30/9/19Establece un sistema de referencia con instante inicial: ti = 0 correspondiente a la partida de los móviles, con origen de coordenadas en Barcelona, y con eje OX con sentido positivo hacia Zaragoza.
Luego, tienes los datos del auto:
ti = 0, xi = 0, vi = 0, a = 10 m/s2;
luego, planteas la ecuación de posición de Movimiento Rectilíneo Uniformemente Variado, reemplazs datos, resuelves coeficientes, y queda.
xa = 5*t2.
Luego, tienes los datos de la moto:
ti = 0, xi = 350 Km = 350000 m, vm = -100 m/s (aquí ten en cuenta el sentido de la velocidad);
luego, planteas la ecuación de posición de Movimiento Rectilíneo Uniforme, reemplazas datos, resuelves coeficientes, y queda.
xm = 350000 - 100*t.
Luego, planteas la condición de encuentro, y queda la ecuación:
xa = xm, sustituyes expresiones, y queda:
5*t2 = 350000 - 100*t, sumas 100*t y restas 350000 en ambos miembros, y queda:
5*t2 + 100*t - 350000 = 0, divides por 5 en todos los términos, y queda:
t2 + 20*t - 70000 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
t = ( -20 - √(280000) )/2 ≅ -274,575 s, que no tiene sentido para este problema;
2°)
t = ( -20 + √(280000) )/2 ≅ 254,575 s ≅ 4,243 min;
luego, remplazas el valor remarcado en las expresiones de las posiciones de los móviles, y queda:
xa ≅ 5*254,5752 ≅ 324042,487 m ≅ 324,042 Km,
xm ≅ 350000 - 100*254,575 ≅ 324542,487 m ≅ 324,542 Km,
y observa que la discrepancia entre estos dos valores se debe a las aproximaciones que hemos empleado.
Luego, puedes concluir que los móviles se encuentran aproximadamente luego de 4,243 minutos de haber partido, y que se cruzan aproximadamente a 324,542 Km de la ciudad de Barcelona.
Espero haberte ayudado.
-
Determinar la tensión en la cuerda AB y las componentes horizontal y vertical de la reacción en el apoyo C, del sistema en equilibrio de la Fig. 4. El cuerpo suspendido tiene una masa de 10 Kg y la barra uniforme BC tiene una masa de 4 Kg.


Antonio Silvio Palmitano
el 30/9/19Vamos con una orientación.
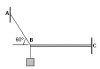
Considera un sistema de referencia con origen de coordenadas en el punto B, con eje OX horizontal con sentido positivo hacia la derecha, con eje OY vertical con sentido positivo hacia arriba, y con sentido de giro positivo antihorario.
Luego, observa que en el punto B de la cuerda están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso del bloque: P = M*g, vertical, hacia abajo;
Tensión de la cuerda: T, hacia arriba y hacia la izquierda, formando 60° con la dirección horizontal;
Acción de la barra: A, horizontal, hacia la derecha;
luego, aplicas la Primera Ley de Newton, y tienes el sistema de ecuaciones:
A - T*sen(60°) = 0,
T*cos(60°) - P = 0,
sustituyes la expresión del módulo del peso del bloque, y queda:
A - T*sen(60°) = 0,
T*cos(60°) - M*g = 0, de aquí despejas: T = M*g/cos(60°);
luego, sustituyes la expresión remarcada en la primera ecuación, aplicas la identidad trigonométrica de la tangente, y luego despejas: A = M*g*tan(60°).
Luego, puedes considerar que la componente horizontal de la reacción de la pared sobre la barra tiene módulo H, con dirección horizontal y sentido hacia la izquierda, que la componente vertical de la reacción de la pared sobre la barra tiene módulo V, con dirección vertical hacia arriba, observa que tienes al peso de la barra (Pb)aplicado en su punto medio, tomas momentos de fuerzas con respecto a un eje perpendicular a la figura que pasa por el punto B (observa que las fuerzas aplicadas en este punto no producen momento, y observa que la componente horizontal de la reacción de la pared tampoco produce momento, aplicas la Primera Ley de Newton para giros, y queda:
L*V - (L/2)*Pb = 0, sustituyes la expresión del peso de la barra, divides por L en todos los miembros, y queda:
V - (1/2)*Mb*g = 0, y de aquí despejas: V = (1/2)*Mb*g.
Luego, observa que las únicas fuerzas horizontales que están aplicadas sobre la barra son la reacción horizontal de la pared (cuyo sentido es hacia la izquierda), cuyo módulo es H, y la reacción de la cuerda (cuyo sentido es hacia la derecha), cuyo módulo es A, por lo que puedes plantear la ecuación:
A - H = 0, de aquí despejas:
H = A, sustituyes la expresión del módulo de la reacción de la cuerda que ya tienes remarcada, y queda:
H = M*g*tan(60°).
Luego, solo queda que reemplaces datos en las dos últimas expresiones remarcadas, y tendrás los valores de los módulos de las componentes de la reacción de la pared sobre la barra; luego, podrás calcular el módulo de la reacción como la resultante de sus componentes, y el valor del ángulo de inclinación (te dejo la tarea).
Haz el intento de terminar la tarea, y si te resulta necesario no dudes en volver a consultar.
Espero haberte ayudado.
-


Francisco Javier
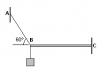
el 30/9/19Tomamos cualquier vértice del triangulo rectángulo para hacer el análisis.
Yo tomare el punto donde se forma el angulo de 30º (presencia de las fuerzas de 10 kg y 20 kg).
Aclaro, el resultado debe ser el mismo, independientemente de este punto que se tome.
Ahora expresamos el cateto opuesto (C.O) y adyacente (C.A), respecto al angulo de 30º, en función de "d".
Esto lo hacemos aplicando trigonometría básica.
Con la identidad seno tenemos que:
Sin(30º) = C.O/d
Despejando "C.O":
C.O = d*Sin(30º)
Con la identidad coseno tenemos que:
Cos(30º) = C.A/d
Despejando "C.A":
C.A = d*Cos(30º)
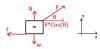
Lo siguiente es descomponer la fuerza de 10 kg presente en lo mas alto del plano.
Por geometría, el angulo "β" que forma esta fuerza respecto al eje horizontal (suelo) es de 60º.
Omito la demostración. Dicho esto:
β = 60º
Entonces:
F10 kg (x) = 10*Cos(60º)
F10 kg (y) = 10*Sin(60º)
Recordamos que el momento de una fuerza se determina aplicando la siguiente ecuación:
M = r*F
Donde "r" es la distancia entre la fuerza y el punto de análisis y "F" es el valor de fuerza.
"r" siempre es perpendicular a "F".
Los momentos en sentido horarios son negativos. Por el contrario, si los momentos van en sentido anti-horario serán positivos.
Aclarado esto, podemos hacer la sumatoria de momentos en el vértice tomado:
∑M = M20 kg + M60 kg + M10 kg (y) + M10 kg (x) = - 40
∑M = 20*C.A - 60*C.A - 10*Sin(60º)*C.A - 10*Cos(60º)*C.O = - 40
Reemplazando los valores de C.A y C.O:
20*d*Cos(30º) - 60*d*Sin(30º) - 10*Sin(60º)*d*Cos(30º) - 10*Cos(60º)*d*Sin(30º) = - 40
Finalmente, despejando para "d" damos por terminado el problema:
d*[20*Cos(30º) - 60*Sin(30º) - 10*Sin(60º)*Cos(30º) - 10*Cos(60º)*Sin(30º)] = - 40
d = - 40/[20*Cos(30º) - 60*Sin(30º) - 10*Sin(60º)*Cos(30º) - 10*Cos(60º)*Sin(30º)]
d = - 40/[- 22.6795]
d = 1.7637 m
-
Buenas noches me podrían ayudar con estos dos problemas
1) Una mujer lleva su valija de 15 Kg a una velocidad constante y su correa forma un ángulo θ respecto de la horizontal. La fuerza con que tira la correa es de 30 N de magnitud y una fuerza de rozamiento horizontal de 18 N actúa también sobre la valija. Determinar: a) el valor del ángulo θ, y b) la fuerza normal que ejerce el piso sobre la valija.
2) Determinar la tensión en la cuerda AB y las componentes horizontal y vertical de la reacción en el apoyo C, del sistema en equilibrio de la Fig. 4. El cuerpo suspendido tiene una masa de 10 Kg y la barra uniforme BC tiene una masa de 4 Kg.


Francisco Javier
el 30/9/191)
Lo primero que debemos hacer es un diagrama de cuerpo libre que muestre todas las fuerzas que actúan sobre la valija.
Dicho diagrama te lo muestro al final de la respuesta.
Todo calculo hecho desde ahora debe respetar el sistema de referencia propuesto en el diagrama.
Aplicaremos en todo el problema la primera ley de newton debido a que hay velocidad constante (no hay aceleración).
Quiere decir que toda sumatoria de fuerzas sera igual a cero.
Haciendo una sumatoria de fuerzas igual a cero en el eje horizontal:
∑Fx = 0
F*Cos(θ) - ƒ = 0
Donde "F" es la fuerza aplicada por la mujer y "ƒ" es la fuerza de fricción.
"F*Cos(θ)" es el valor de la componente horizontal de la fuerza "F".
Reemplazando los datos y despejando para "θ":
30*Cos(θ) - 18 = 0
30*Cos(θ) = 18
Cos(θ) = 18/30
θ = Cos-1(18/30)
θ = 53.1301º
Haciendo una sumatoria de fuerzas igual a cero en el eje vertical:
∑Fy = 0
N - w = 0
Donde "N" es la fuerza normal y "w" es el peso de la valija.
Recuerda que:
w = m*g
Entonces:
N - m*g = 0
Reemplazando datos y despejando para "N" acabamos el problema:
N = m*g
N = 15*9.81
N = 147.15 N
Diagrama:
2)
Se hace mención a una figura la cual no anexas. Sin esta información, el problema no se puede resolver.
-
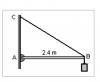
La barra uniforme AB de la Fig. 3 tiene una masa de 3 Kg, su extremo B está sujeto por un cable BC de 3.2 m de longitud y sostiene un cuerpo de 6 Kg. Calcular la tensión del cable BC y las componentes horizontal y vertical de la fuerza ejercida por la pared sobre el extremo A de la barra.


Francisco Javier
el 30/9/19Hacemos el diagrama de cuerpo libre para todo el sistema.
Dicho diagrama te lo muestro al final de la respuesta.
Todo calculo hecho desde ahora debe respetar el sistema de referencia propuesto en el diagrama.
Haciendo una sumatoria de momentos igual a cero en el punto "o" (ver diagrama):
Mo = - wobjeto*2.4 - wbarra*1.2 + BCy*2.4 + BCx*c = 0
Donde "BCy" y "BCx" son componentes de la fuerza de tensión "BC" vertical y horizontal respectivamente.
"w" es peso y "c" es la distancia entre la componente "BCx" y la barra o punto cero.
Esta ultima incógnita sale aplicando pitagoras:
h2 = c2 + l2
Del diagrama y enunciado:
h = 3.2 m
l = 2.4 m
Reemplazando y despejando para "c":
3.22 = c2 + 2.42
c2 = 3.22 - 2.42
c = 2.1166 m
Hacemos recordar que la barra reflejara su peso en su punto central.
Como:
w = m*g
Quedaría:
Mo = - mobjeto*g*2.4 - mbarra*g*1.2 + BCy*2.4 + BCx*2.1166 = 0
Podríamos poner las componentes en función de la fuerza "BC" sabiendo que:
BCy = BC*Sin(θ)
BCx = BC*Cos(θ)
Donde "θ" es el angulo que forma la cuerda BC con la barra. Su determinación se hace con trigonometría básica.
Buscamos la identidad que nos relaciona el cateto adyacente (l) y la hipotenusa (h)
Dicha identidad es coseno.
Dicho esto:
Cos(θ) = l/h
Como ya definimos anteriormente:
l = 2.4 m
h = 3.2 m
Entonces:
Cos(θ) = 2.4/3.2
Despejando para "θ":
θ = Cos-1(2.4/3.2)
θ = 41.4096º
Entonces:
BCy = BC*Sin(θ) = BC*Sin(41.4096º) = 0.6614*BC
BCx = BC*Cos(θ) = BC*Cos(41.4096º) = 0.75*BC
Reemplazando esto en la ecuación de momento quedaría finalmente:
Mo = - mobjeto*g*2.4 - mbarra*g*1.2 + 0.6614*BC*2.4 + 0.75*BC*2.1166 = 0
Reemplazando datos y despejando para "BC":
- 6*9.81*2.4 - 3*9.81*1.2 + 0.6614*BC*2.4 + 0.75*BC*2.1166 = 0
0.6614*BC*2.4 + 0.75*BC*2.1166 = 6*9.81*2.4 + 3*9.81*1.2
BC*(0.6614*2.4 + 0.75*2.1166) = 6*9.81*2.4 + 3*9.81*1.2
BC = (6*9.81*2.4 + 3*9.81*1.2)/(0.6614*2.4 + 0.75*2.1166)
BC = 55.6191 N
Y con este valor ya podemos saber también las componentes en los eje verticales y horizontales.
BCy = BC*Sin(θ) = 55.6191*Sin(41.4096º) = 36.7886 N
BCx = BC*Cos(θ) = 55.6191*Cos(41.4096º) = 41.7143 N
Haciendo una sumatoria de fuerzas en el eje vertical igual a cero:
∑Fy = 0
Ay + BCy - wobjeto - wbarra = 0
Ay + BCy - mobjeto*g - mbarra*g = 0
Reemplazando datos y despejando para "Ay":
Ay + 36.7886 - 6*9.81 - 3*9.81 = 0
Ay = 3*9.81 + 6*9.81 - 36.7886
Ay = 51.5014 N
Haciendo una sumatoria de fuerzas en el eje horizontal igual a cero:
∑Fx = 0
Ax - BCx = 0
Reemplazando datos y despejando "Ax" terminamos el problema:
Ax - 41.7143 = 0
Ax = 41.7143 N
Diagrama:
-
por favor me podrian ayudar en estos dos dos ultimos problemas
1) La suma de dos vectores A y B tiene
un módulo de 90 unidades y forma un ángulo de 130º con el vector A. Si el
módulo del vector A es de 100 unidades, determinar:a) el módulo
del vector y b) el
ángulo que forman A y B.2) Una persona está a 90 m de su campamento
en la dirección SO. En cierto instante camina 200 m hacia el Norte, y luego cambia
de rumbo hacia el SE, avanzando esta vez 150 m. Si decide regresar al campamento,
determinar el desplazamiento que lo llevará directamente al campamento.


Francisco Javier
el 30/9/191)
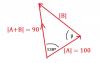
Dibujamos los tres vectores de tal manera que se nos forme un triangulo de vectores.
Dicho dibujo te lo dejo al final de la respuesta.
Aplicando la ley de cosenos determinamos el valor de la magnitud del vector B.
Si nos recuerdas esta ley, te dejo una imagen al final donde podrás ver como aplicarla.
Dicho esto:
|B|2 = |A|2 + |A + B|2 - 2*|A|*|A + B|*Cos(θ)
|B|2 = 1002 + 902 - 2*100*90*Cos(130º)
|B|2 = 29670.2
|B| = 172.25 unidades
Y para determinar el angulo que forman los vectores A y B aplicamos ahora la ley de senos.
Si no recuerdas esta ley, te dejo una imagen al final donde podrás ver como aplicarla.
Dicho esto:
Sin(β)/90 = Sin(130º)/172.25
Y despejando para "β" terminamos el problema:
Sin(β) = [Sin(130º)/172.25]*90
Sin(β) = 0.4003
β = Sin-1(0.4003)
β = 23.5969º
Triangulo de vectores:
Ley de senos y cosenos:


Francisco Javier
el 30/9/192)
Expresamos todos los vectores dados en sus componentes rectangulares.
Primero vector (A): 90 metros hacia el NE (45º)
Ax = A*Cos(θ) = 90*Cos(45º) = 63.6396 m
Ay = A*Sin(θ) = 90*Sin(45º) = 63.6396 m
Segundo vector (B): 200 metros hacia el N
Bx = 0 m
By = 200 m
Tercer vector (C): 150 metros hacia el SE (45º)
Cx = C*Cos(θ) = 150*Cos(45º) = 106.066 m
Cy = - C*Sin(θ) = - 150*Sin(45º) = - 106.066 m
Calculamos el vector resultante (R) que va desde el campamento hasta la punta del vector C.
Esto se halla sumando las componentes por ejes:
Rx = Ax + Bx + Cx = 63.6396 + 0 + 106.066 = 169.706 m
Ry = Ay + By + Cy = 63.6396 + 200 - 106.066 = 157.574 m
R = Rx + Ry = 169.706 i + 157.574 j [m]
Pero como nosotros deseamos saber el vector contrario (de la punta de C al campamento), multiplicamos por - 1.
R' = - R = - 169.706 i - 157.574 j [m]
Este es el vector que describe el desplazamiento que debe tomar la persona para volver al campamento.
Calculamos la magnitud de este vector para dar por concluido el problema:
|R'| = [(- 169.706)2 + (- 157.574)2]0.5 = 231.581 m
-
hola me pueden ayudar con estos dos problemas
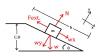
1) Una caja de masa 110 Kg ha de bajarse de un camión que tiene 1.3 m de altura, haciéndola deslizar con velocidad constante sobre un tablón liso de 3.0 m de longitud. Determinar la fuerza paralela al plano necesaria y la reacción normal del tablón.
2) Un jugador de golf mete su pelota en un hoyo en tres golpes. El primer golpe desplaza la pelota 9 m hacia el Norte, el segundo 6 m hacia el Sureste y el tercero 2 m hacia el Suroeste. Determinar el desplazamiento que será necesario para meter la bola de un solo golpe.


Francisco Javier
el 30/9/191)
Realizamos un diagrama de cuerpo libre de la caja.
Dicho diagrama de lo muestro al final de la respuesta.
Problema de primera ley de newton. Toda sumatoria sera igual a cero.
Determinamos primero el angulo que tendrá el tablón respecto al piso.
Esto sale aplicando trigonometría básica.
Buscamos la identidad que nos relaciona el cateto opuesto (C.O) con la hipotenusa (h).
Dicha identidad es el seno.
Matemáticamente:
Sin(θ) = C.O/h
Del enunciado del problema:
C.O = 1.3 m
h = 3.0 m
Reemplazando valores y despejando para "θ":
Sin(θ) = 1.3/3.0
θ = Sin-1(1.3/3.0)
θ = 25.6793º
Teniendo este angulo, podemos ahora descomponer al componente del peso de la caja paralela al tablón "wx".
Para planos inclinados con angulo de inclinación respecto a la horizontal se cumple siempre que:
wx = w*Sin(θ)
wy = w*Cos(θ)
Como:
w = m*g
Tenemos que:
wx = m*g*Sin(θ)
wy = m*g*Cos(θ)
Reemplazando datos:
wx = 110*9.81*Sin(25.6793º) = 467.61 N
wy = 110*9.81*Cos(25.6793º) = 972.521 N
Haciendo una sumatoria de fuerzas paralelas al plano igual a cero:
∑Fx = 0
- Fexterna + wx = 0
Reemplazando datos y despejando para "Fexterna":
- Fexterna + 467.61 = 0
Fexterna = 467.61 N
Quiere decir que para poder bajar la caja a velocidad constante, la fuerza aplicada debe ser igual a la componente del peso paralela al plano.
Haciendo una sumatoria de fuerzas perpendiculares al plano igual a cero:
∑Fy = 0
N - wy = 0
Reemplazando datos y despejando para "N" terminamos el problema:
N - 972.521 = 0
N = 972.521 N
Diagrama:


Francisco Javier
el 30/9/192)
Expresamos en sus componentes rectangulares cada vector.
Primero vector (A): 9 metros hacia el N.
Ax = 0 m
Ay = 9 m
Segundo vector (B): 6 metros hacia el SE (45º).
Bx = B*Cos(45º) = 6*Cos(45º) = 4.2426 m
By = - B*Sin(45º) = - 6*Cos(45º) = - 4.2426 m
Tercer vector (C): 2 metros hacia el SO (45º).
Cx = - C*Cos(45º) = - 2*Cos(45º) = - 1.4142 m
Cy = - C*Sin(45º) = - 2*Sin(45º) = - 1.4142 m
El vector resultante (R) se calcula sumando las componentes rectangulares por eje:
Rx = Ax + Bx + Cx = 0 + 4.2426 - 1.4142 = 2.8284 m
Ry = Ay + By + Cy = 9 - 4.2426 - 1.4142 = 3.3432 m
R = Rx + Ry = 2.8284 i + 3.3432 j [m]
Este sera el vector que representa el desplazamiento que debe tener la pelota para hacer hoyo en uno de un solo golpe.
Calculamos la magnitud de este vector desplazamiento para terminar el problema:
|R| = [(2.8284)2 + (3.3432)2]0.5 = 4.3791 m
-
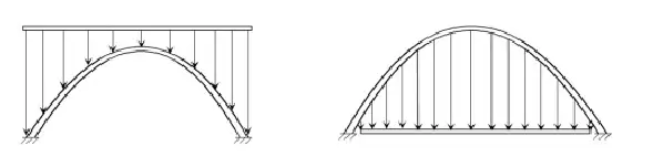
Buenas. ¿Alguien puede darme una pequeña explicación física sobre el funcionamiento de los arcos en las construcciones? Creo que tiene que ver con la línea de empujes, así que si pudieran aclararme ese lugar geométrico...
¿Cómo es que todas esas fuerzas verticales sobre el arco, recaen finalmente en sus apoyos?