-
Me he fijado en que los resultados no me dan, y que posiblemente sea porque no he tenido en cuenta la altura, pero esa altura, en teoría, solo lo da energía potencial y no hay movimiento en su eje.
-
En un pabellon de futbol sala, 1000 espectadores gritan al mismo tiempo, con un nivel de intensidad de 60dB cada uno, cual es el nivel de intensidad sonora que producen todos juntos?


Raúl RC
el 24/6/19Hola Fátima, siempre os decimos que debéis adjuntar los pasos que hayáis podido hacer para que podamos ver en qué falláis y qué no entendéis (solo adjuntando el enunciado no es suficiente).
Por otra parte te recuerdo que antes de formular vuestras preguntas disponeis de más de 700 vídeos explicativos en la web en la que en la mayor parte d elos casos vuestras dudas ya han sido tratadas en un vídeo explicativo por el profe, como éste:
Simplemente que lo tengas en cuenta para la próxima vez ok? ;)
Intensidad de sonido DecibelioRespecto a tu problema:
Aplicas la expresión de la intensidad de sonido:
β=10log(I/I0) siendo I0=10-12W/m2
Lo que tenemos como dato es la intensidad de sonido de un espectador, es decir, β=60 dB, por tanto ,hallamos la I correspondiente a ese sonido:
60=10log(I/10-12) =>I=10-6W/m2
Finalmente para 1000 espectadores será:
I1000 espectadores=1000·10-6=10-3W/m2
Para acabar volvemos a calcular el nivel de intensidad sonora que producen todos los espectadores a la vez:
β=10log(I/I0)=10log(10-3/10-12)=90 dB
Mejor? ;)
-


Raúl RC
el 24/6/19Hola Sol, desconozco ese método, al menos por ese nombre, pero si te refieres a realizar un diagrama de cuerpo libre, aquí tienes un ejemplo que el profe ya grabó ;)
Diagrama del cuerpo libre 01 -
 Hola, una consultita, solo tengo duda porque es negativo el t1, si el bloque esta cayendo, no sería positivo, por fa, una explicación, lo considera el profesor que es negativo, ( considerar que t1 es la tensión que esta unido al bloque, cuando el bloque cae, y t2 es la tensión de la izquierda (t2 es la continuación de t1 a mi forma de ver))
Hola, una consultita, solo tengo duda porque es negativo el t1, si el bloque esta cayendo, no sería positivo, por fa, una explicación, lo considera el profesor que es negativo, ( considerar que t1 es la tensión que esta unido al bloque, cuando el bloque cae, y t2 es la tensión de la izquierda (t2 es la continuación de t1 a mi forma de ver))En resumen alguien me puede explicar porque t1 es de signo negativo (t1 es el torque 1 (que es el mg más masa por la aceleracion))


Raúl RC
el 24/6/19Es negativo por el convenio de signos que se escoge a la hora de establecer el giro, se considera torque positivo cuando el sentido es antihorario y negativo cuando es horario, si te fijas la tensión T1 hace girar a la pole en sentido horario, con lo cual signo negativo ;)
Espero haberte ayudado ;)
-
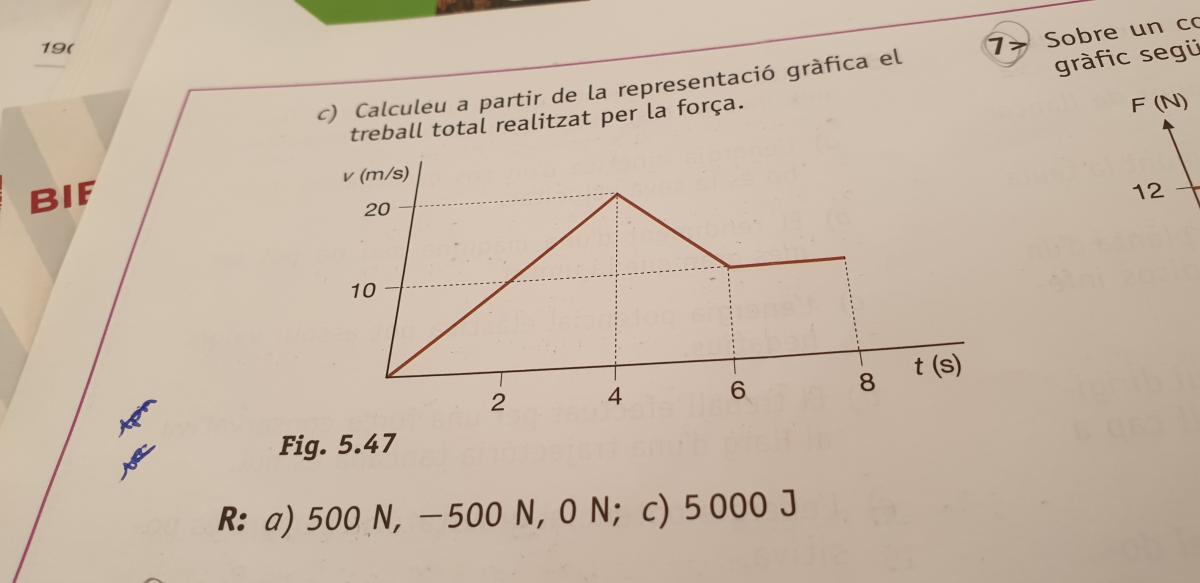

El problema es que en el segundo enunciado el trabajo de la segunda fuerza ya me da 5000J justos, y el total 25000J
 Calcular-lo*
Calcular-lo*


Raúl RC
el 24/6/19a) Primer tramo:
aceleracion => a=v-v0/t-t0=5 m/s2
Con ello F=m·a= 100·5=500 N
Segundo tramos:
aceleración: =>a=a=v-v0/t-t0=10-20/6-4=-5 m/s2
Con ello F=m·a= 100·(-5)=-500 N
3º tramo a=0 m/s2 con lo cual F=0 N
b) Te lo dejo a ti
c) Aplicas la expresión W=F·d siendo d la distancia recorrida en metros en cada tramo, para ellos deberás aplicar las expresiones del MRUA en el 1º y 2º tramos y la del MRU en el 3º ya que en este último v= cte
Finalmente sumas todos esos trabajos y obtendrás el trabajo total
A por ello ;)
-


Raúl RC
el 24/6/19WFR=FR·d·cos180 ya que la fuerza es contraria al desplazamiento por eso el ángulo es 180º
WFR=μN·d·cos180
La fuerza normal la calculamos teniendo en cuenta las fuerzas que actúan sobre el eje Y (debes descomponer las fuerzas previamente):
ΣFy=m·a=0 =>N+Fy=P=>N=P-Fy=mg-25·sen45
Reemplzando:
WFR=μN·d·cos180=-0,1·(2·9,8-25·sen45)·5=-0,9611 J
Para entender lo que he hecho debes ver este vídeo sí o sí
https://www.youtube.com/watch?v=50GUrSoGUIk
Un saludo ;)
-
¿La energía potencial gravitatoria puede ser negativa? Yo creo que depende de la altura que usemos cómo referencia. Por ejemplo si tomas el nivel del suelo como el punto y=0 y hablamos de un pozo


Raúl RC
el 23/6/19La energía potencial gravitatoria NUNCA puede ser negativa, lo que va a ser negativo es la VARIACIÓN de ésta entre dos puntos.
De hecho se dice que es negativa porque PREVIAMENTE hemos asignado que esta energia es cero en el infinito, con lo cual, a medida que la masa se acerque la energía siempre disminuirá.
-





































