-

Guillem De La Calle Vicente
el 24/6/19Exercici 1) En total es produeixen 110.000.000 kWh. Hi ha 37 aerogeneradors de 1300 kW, per tant, es produeixen 37·1300 = 48100 kW. El nombre d'hores de funcionament efectives en un any es de 110.000.000/48100 = 2286,90 h.
Exercici 2) Saps que els 3500 MW són d'energia eòlica i formen el 12,3% de la producció bruta d'electricitat. Per tant, la producció bruta d'electricitat és de:
12,3% de x = 3500 --> 12,3/100 · x = 3500 --> x = 3500·100 / 12,3 = 28455,28 MW.
-
He calculado la energía cinética y después he calculado el trabajo, pero la potencia no concuerda con el resultado


Raúl RC
el 23/6/19No te piden la potencia.
Te recomiendo leer el enunciado varias veces para que tomes conciencia de lo que te piden, anotar los datos y finalmente las expresiones matemáticas que vas a tener que utilizar para dar con las soluciones:
a) Aplicas la ley de Hooke:
F=k·x
m·g=k·x
25·9,8=2500·x => x=0,098 m
b) la energia potencial elástica se define como:
E=0,5·k·x2=0,5·2500·0,0982= 12J
P.D: Recuerda adjuntar tu procedimiento, no vale solo con aportar el enunciado, queremos ver qué has hecho ;)
-


Raúl RC
el 23/6/19Te recomiendo que plantees el problema por tramos y siempre aplicando conservación de la energia (excepto en el tramo donde hay rozamiento)
Por ejemplo entre A y B:
Epelástica+EpA=EpB+EcB
0,5·k·x2+mghA=mghB+0,5·m·vB2
Como hA=hB entonces se anulan esos términos, con lo cual:
0,5·k·x2=0,5·m·vB2
Podemos hallar vB:
0,5·1000·0,12=0,5·10·vB2
vB= 1 m/s
A partir de aquí te recomiendo vayas aplicando la misma operación en cada tramo, lo único que tendrás que tener en cuenta es el tramo donde hay rozamiento, ahí no se cumple la conservación de la energía si no que se cumple que el trabajo de la fuerza de rozamiento es igual a la variación de la energía mecánica, matemáticamente:
WFR=ΔEm=Emf-Emi
Este vídeo puede ayudarte también, inténta resolverlo con las directrices que te he dado y nos cuentas ok? ;)
https://www.youtube.com/watch?v=JvQY85uPF54
-


Raúl RC
el 23/6/19a) el trabajo para liberarlo es de tipo energia potencial elastica:
W=Epe=0,5·k·x2=0,5·560·0,252= 17,5 J
b) A su vez ese trabajo inicial se invierte en imprimirle una velocidad a la bola, es decir, una energia cinética inicial, con lo cual aplicando conservación de la energía:
Epe=Ec
17,5=0,5·m·vi2=>vi= 24,15 m/s
c) Finalmente aplicando las expresiones del MRUA y teniendo en cuenta que la velocidad a la que se produce la altura máxima es cero:
vf2=vi2-2gh (el signo menos es porque la gravedad es negativa)
0=24,152-2·9,8·h =>h=29,76 m
Mejor? ;)
-


Francisco Javier
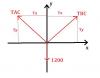
el 23/6/19Tenemos la tensión TAC, y la tensión TBC, las cuales por el enunciado son iguales:
TAC = TBC
Además mencionan que estas tensiones antes mencionadas no deben ser mayor a 870 N.
Dicho esto, tenemos la condición que:
TAC = TBC = 870 N
Lo siguiente es realizar un diagrama de cuerpo libre de la situación (te el bosquejo nada profesional abajo).
Haciendo sumatoria de fuerzas en el eje vertical igual a cero, debido a que hay equilibrio, tenemos que:
∑Fy = 0
2*Ty - 1200 = 0
2*Ty = 1200
Ty = 600 N
Una vez obtenido el valor de esta componente vertical, y teniendo ya el valor del vector principal, podemos aprovechar la configuración (triángulo rectángulo) para hallar la componente horizontal con el teorema de pitágoras. Dicho esto:
TAC2 = Tx2 + Ty2
8702 = Tx2 + 6002
Tx2 = 8702 - 6002
Tx = (8702 - 6002)0.5
Tx = 630 N
Ahora podemos hacer una relación fuerza - longitud en el triángulo rectángulo de tal manera que:
TAC/LAC = Tx/Lx
Donde LAC es la longitud del cable AC y Lx es la longitud horizontal del triángulo rectángulo.
Reemplazando datos:
870/LAC = 630/2.1
Y despejando para LAC:
LAC = (2.1/630)*870
LAC = 2.9 m
Y como la longitud del cable AC es igual a la del cable BC, multiplicamos por dos este resultado para hallar la respuesta.
LACB = 2*LAC
LACB = 2*2.9
LACB = 5.8 m
-
una locomotora de un tren de mercancías ejerce una fuerza de 5 newton sobre el tren, mientras lo arrastra sobre una vía horizontal a la velocidad de 40 km/h.¿cuantos kg.m de trabajo realiza la locomotora es un recorrido de 1 km?
-
desde una altura de 70 cm cae cada segundo una gota de agua que pesa 1/4 de gramo. calcular el trabajo que es capaz de realizar la gotera en un año
-
en un canal de 2m de profundidad y 5 m de ancho fluye el agua con una velocidad media de 100 cm/ seg. calcular en C.V., la potencia de la corriente.


Raúl RC
el 21/6/19No nos dicen nada pero es de entender que el canal tiene forma cilindrica, con lo cual necesitarás en primer lugar el volumen de la tubería:
V=π·r2·h=π·(2,5)2·2=39,26 m3
Con esto y la expresión de la densidad del agua( dagua=1000 kg/m3) podemos averiguar la masa del agua:
d=m/V=>m=d·V=1000·39,26=39260 kg
Finalmente aplicando la expresión de la potencia y teniendo en cuenta la definición de trabajo (1CV=736W):
P=W/t=F·x/t=F·v=m·g·v=39260·9,8·1=384748 W=522,75 CV
-
un jornalero carga en media hora 1 m3 de tierra, debiendola levantar a 1.5 m de altura .¿ que potencia en H.P ha desarrollado ? dato : 1 m3 de tierra pesa 1.8 toneladas .