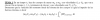-


Antonio Silvio Palmitano
el 27/5/19Considera un instante, y establece un sistema de referencia con origen de coordenadas en la posición de la piedra, con eje OX horizontal con sentido positivo hacia el eje de giros, y con eje OY vertical con sentido positivo hacia arriba.
Luego, observa que sobre la piedra están aplicadas dos fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g = 2*9,8 = 19,6 N, vertical, hacia abajo;
Tensión de la cuerda: T, inclinada, hacia el eje de giros y hacia arriba, determinando un ángulo de 30° con el eje OY;
luego, aplicas la Segunda Ley de Newton, y tienes el sistema de ecuaciones:
T*sen(30°) = M*acp,
T*cos(30°) - P = 0, de aquí despejas: T = P/cos(30°) = 19,6/cos(30°) ≅ 22,632 N;
luego, reemplazas valores en la primera ecuación, y queda:
22.632*sen(30°) ≅ 2*acp, de aquí despejas: acp ≅ 22,632*sen(30°)/2 ≅ 5,658 m/s2;
luego, sustituyes la expresión del módulo de la aceleración centrípeta, y queda:
v2/R ≅ 5,658, reemplazas el valor del radio de la trayectoria (R = 40 cm = 0,4 m) y queda:
v2/0,4 ≅ 5,658, multiplicas por 0,4 en ambos miembros, y queda:
v2 ≅ 2,263, extraes raíz cuadrada positiva, y queda:
v ≅ 1,504 m/s.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 27/5/19Observa que sobre el tablón están aplicadas cuatro fuerzas verticales, de las que indicamos sus módulos y sentidos:
Fuerza ejercida por John: FJ, hacia arriba,
Fuerza ejercida por Marsha: FM, hacia arriba,
Acción del peso del cuerpo: P = 60*9,8 = 588 N, hacia abajo,
Peso del tablón: PT = 10*9,8 = 98 N, hacia abajo;
luego, aplicas la Primera Ley de Newton, y tienes la ecuación:
FJ + FM - P - PT = 0, reemplazas valores, y queda:
FJ + FM - 588 - 98 = 0, reduces términos semejantes, y queda:
FJ + FM - 686, sumas 686 en ambos miembros, y queda:
FJ + FM = 686 (1) (en newtons).
Luego, considera los momentos que producirían cada una de las fuerzas, con respecto al extremo del tablón que sujeta John, de las cuáles indicamos sus módulos y giros que provocarían:
MJ = 0 (la fuerza ejercida por John está aplicada en el extremo del tablón),
MM = L*FM = (2,5+1,5)*FM = 4*FM (en N*m), antihorario,
MP = 2,5*P = 2,5*588 = 1470 N*m, horario,
MPT = (L/2)*PT = 2*98 = 196 N*m, horario;
luego, aplicas la Primera Ley de Newton para giros, y queda:
MJ + MM - MP - MPT = 0, sustituyes expresiones, y queda:
0 + 4*FM - 1470 - 196 = 0, reduces términos numéricos, y queda:
4*FM - 1666 = 0, y de aquí despejas: FM = 416,5 N;
luego, reemplazas este último valor remarcado en la ecuación señalada (1), y queda:
FJ + FM = 686, restas x en ambos miembros, y queda:
FJ = 686 - FM, reemplazas el valor remarcado, y queda:
FJ = 686 - 416,5, aquí resuelves, y queda: FJ = 269,5 N.
Espero haberte ayudado.
-
Una caja de 2m3 y de masa uniforme está apoyada sobre un tablón de madera de ángulo x que va aumentando lentamente. El coeficiente de rozamiento evita que la caja se caiga o deslice. Cuál es el máximo valor que puede alcanzar el ángulo sin que se caiga la caja?


Antonio Silvio Palmitano
el 27/5/19Considera que la caja es una partícula, y considera la situación crítica (la caja está a punto de deslizarse), y observa que sobre la caja están aplicadas tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso: P = M*g, vertical, hacia abajo,
Acción normal del tablón: N, perpendicular al tablón, hacia arriba,
Rozamiento estático del tablón: fre = μe*N, paralela al tablón, hacia arriba.
Luego, establece un sistema de referencia con eje OX paralelo al tablón con sentido positivo hacia abajo, y con eje OY perpendicular al tablón con sentido positivo hacia arriba, aplicas la Primera Ley de Newton (observa que el peso de la caja forma un ángulo θ con el semieje OY negativo), y queda el sistema de ecuaciones:
P*senθ - fre = 0,
N - P*cosθ = 0;
luego, sustituyes las expresiones de los módulos del peso y del rozamiento estático, y queda:
M*g*senθ - μe*N = 0,
N - M*g*cosθ = 0, y de aquí despejas: N = M*g*cosθ;
luego, sustituyes esta última expresión en la primera ecuación, y queda:
M*g*senθ - μe*M*g*cosθ = 0, divides por M y por g en todos los términos, y queda:
senθ - μe*cosθ = 0, sumas μe*cosθ en ambos miembros, y queda:
senθ = μe*cosθ, divides por cosθ en ambos miembros, aplicas la identidad trigonométrica de la tangente, y queda:
tanθ = μe, aquí compones con la función inversa de la tangente, y queda:
θ = arctan(μe).
Luego, si debes considerar que la caja no es una partícula, entonces deberías conocer cuál es su ancho, su largo y su altura para plantear el problema, cosa que no podemos hacer aquí porque solamente tenemos al volumen de la caja como dato de tu enunciado.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 27/5/19Tienes los datos:
t1i = 0 °C (temperatura inicial de la masa de hielo y del calorímetro),
Lf = 80 cal/g (calor latente de fusión del agua),
M1 = a determinar (masa de hielo),
Cc = 20 cal/°C (capacidad calorífica del calorímetro),
M2 = 76 g (masa inicial de agua),
t2i = 60 °C (temperatura inicial de la masa de agua),
c = 1 cal/(°C*g) (calor específico del agua en estado líquido),
tf = 40 °C (temperatura final del sistema).
Luego, planteas la expresión de la cantidad de calor absorbida por el calorímetro y la masa inicial de hielo (observa que ésta cambia de estado), y queda:
Qabs = M1*Lf + M1*c*(tf - t1i) + Cc*(tf - t1i), reemplazas valores, y queda:
Qabs = M1*80 + M1*1*(40 - 0) + 20*(40 - 0), resuelves términos y coeficientes, y queda:
Qabs = M1*80 + M1*40 + 800, reduces términos semejantes, y queda:
Qabs = M1*120 + 800 (1) (en calorías).
Luego, planteas la expresión de la cantidad de calor cedida por la masa inicial de agua (observa que ésta no cambia de estado), y queda:
Qced = M2*c*(tf - t2i), reemplazas valores, y queda:
Qced = 76*1*(40 - 60), resuelves, y queda:
Qced = -1520 cal (2).
Luego, si consideras que el sistema es cerrado y no tiene pérdidas de calor hacia el ambiente, por lo que puedes plantear que la variación total de energía del sistema es igual a cero, y tienes la ecuación:
Qabs + Qced = 0, sustituyes las expresiones señaladas (1) (2), y queda:
M1*120 + 800 + (-1520) = 0, reduces términos numéricos, y queda:
M1*120 - 720 = 0, sumas 720 en ambos miembros, y queda:
M1*120 = 720, divides por 120 en ambos miembros, y queda:
M1 = 6 g.
Espero haberte ayudado.
-
Necesito ver como se hacen las siguientes cuestiones:
LANZAMOS UNA PELOTA HACIA ARRIBA CON UNA VELOCIDAD DE 20M/S. LA MASA DE LA PELOTA ES DE 100 GRAMOS
1)¿Cuál es la altura máxima que alcanza?


Breaking Vlad
el 26/5/19Sabiendo que la aceleración de la gravedad es -9,8m/s2
calcula el tiempo que tarda la pelota en pasar de 20m/s a 0m/s (altura máxima) y entonces calcula la distancia que ha recorrido hasta llegar a ese punto.
Las ecuaciones son todas las que se usan en este tema, pero sin tener en cuenta el movimiento en el eje x:
-
Buenos días, necesito ayuda con las siguientes preguntas:
1) La masa conjunta de un ciclista y su bicicleta es 70 kg. Se encuentra detenido en una cuesta a 140m de altura
A)El ciclista se deja caer. ¿Qué energías potencial y cinética tendrá cuando vaya por la mitad de la cuesta?
B) ¿Qué energía cinética tendrá cuando llegue al final de la cuesta?
C) ¿Con qué velocidad llegará al final de la cuesta?
Gracias y un saludo.


Breaking Vlad
el 26/5/19Hola Sergio,
te recomiendo este vídeo:
Principio de conservación de la energía mecánica
Una vez lo veas, se trata de que intentes resolver el ejercicio por tu cuenta, y entonces nos preguntes dudas más concretas.
Un saludo
-


Raúl RC
el 24/5/19Lamento no poder ayudarte pero no resolvemos dudas universitarias que no tengan que ver con el nivel general de unicoos, en este caso secundaria y bachiller.
Hay videos sobre colisiones que espero puedan ayudarte ;)
Lo lamento
Momento lineal. Choques

Antonio Silvio Palmitano
el 28/5/19Vamos con un esquema a modo de orientación.
A partir de la Segunda Ley de Newton tienes:
MA*aA + MB*aB = ∑ Fext(t),
expresas a las aceleraciones de las partículas como las derivadas de sus velocidades con respecto al tiempo, y queda:
MA*dvA/dt + MB*dvB/dt = ∑ Fext(t),
separas variables (velocidades, fuerzas que dependen del tiempo, y tiempo: "multiplicas" en todos los términos por dt), y queda:
MA*dvA + MB*dvB = ∑ Fext(t)*dt,
integras (expresamos con corchetes que debes evaluar con Regla de Barrow en el primer miembro), y queda:
MA*[vA] + MB*[vB] = ti∫tf ∑ Fext(t)*dt,
evalúas las expresiones de las velocidades entre sus valores iniciales y finales, y queda:
MA*(vAf - vAi) + MB*(vBf - vBi) = ti∫tf ∑ Fext(t)*dt,
distribuyes términos en el primera miembro, y queda:
MA*vAf - MA*vAi + MB*vBf - MB*vBi = ti∫tf ∑ Fext(t)*dt,
ordenas términos, y queda:
MA*vAf + MB*vBf - MA*vAi - MB*vBi = ti∫tf ∑ Fext(t)*dt,
asocias los dos primeros términos, extraes factor común entre los dos últimos términos, y queda:
(MA*vAf + MB*vBf) - (MA*vAi + MB*vBi) = ti∫tf ∑ Fext(t)*dt.
Espero haberte ayudado.
-
Hola me pueden ayudar con esto?
Dados los vectores A = 8i +2j + 2k, B = 4i + 2j + 4k, C = 6i + 8j + 10 k, calcule el producto (A + B). (B + C).


Antonio Silvio Palmitano
el 24/5/19Esta consulta es propia del Foro de Matemáticas, pero igualmente ahí vamos.
Planteas la expresión del primer factor del producto escalar de tu enunciado, y queda:
A + B = (8i+2j+2k) + (4i +2j+4k) = (8+4)i + (2+2)j + (2+4)k = 12i + 4j + 6k (1).
Planteas la expresión del segundo factor del producto escalar de tu enunciado, y queda:
B + C = (4i +2j+4k) + (6i+8j+10k) = (4+6)i + (2+8)j + (4+10)k = 10i + 10j + 14k (2).
Luego, planteas la expresión del producto escalar de tu enunciado, y queda:
(A+B)•(B+C) =
sustituyes las expresiones señaladas (1) (2), y queda:
= (12i + 4j + 6k)•(10i + 10j + 14k) =
desarrollas el producto escalar, y queda:
= 12*10 + 4*10 + 6*14 =
resuelves términos, y queda:
= 120 + 40 + 84 =
resuelves, y queda:
= 244.
Espero haberte ayudado.
-


Antonio Silvio Palmitano
el 23/5/19Observa que tienes la expresión vectorial de un campo eléctrico constante, cuya dirección y sentido son los que corresponden al eje OY positivo, cuya expresión puedes escribir:
E = < 0 , k > (en N/C),
donde k = 1/(4πε0) = 9*109 es el valor numérico de la constante de Coulomb.
Luego, observa que tienes una carga puntual cuyo valor es: q = -1 (en C), ubicada en el origen de coordenadas.
Y observa que para que el campo eléctrico producido por esta carga pueda equilibrar al campo señalado anteriormente, debe cumplirse que su dirección y sentido correspondan al semieje OY negativo, y observa que esta situación se verifica solamente en los puntos del eje OY cuya ordenada es positiva.
Luego, puedes llamar P(0,y) al punto que debes determinar, y para él tienes que la carga puntual produce en él un campo cuya expresión es:
E1 = < 0 , k*q/y2) = < 0 , k*(-1)/y2) = < 0 , -k*/y2 > (1) (en N/C).
Luego, planteas la condición de campo resultante nulo en el punto P(0,y), y queda la ecuación vectorial:
E + E1 = < 0 , 0 >, sustituyes expresiones, y queda:
< 0 , k > + < 0 , -k*/y2 > = < 0 , 0 >, resuelves la suma vectorial, y queda:
< 0 , k-k*/y2 > = < 0 , 0 >;
luego, por igualdad entre expresiones vectoriales, y teniendo en cuenta que las primeras componentes son nulas en ambos miembros, igualas las expresiones de las segundas componentes, y queda la ecuación escalar:
k - k*/y2 = 0, divides por k en todos los términos, y queda:
1 - 1/y2 = 0, sumas 1/y2 en ambos miembros, y queda:
1 = 1/y2, multiplicas por x en ambos miembros (observa que la incógnita y no puede tomar el valor cero), y queda:
y2 = 1, aquí extraes raíz cuadrada en ambos miembros, y tienes dos opciones:
a)
y = -1 m,
que no tiene sentido para este problema, ya que en el punto Pa(0,-1) los dos campos tendrían la dirección y el sentido del semieje OY positivo y, por lo tanto, no se anularían;
b)
y = 1 m,
que sí tiene sentido para este problema, ya que en el punto Pb(0,1) los campos tienen la dirección del eje OY, con sentidos opuestos, y sus expresiones son (aquí debes tener en cuenta la expresión señalada (1) del campo eléctrico producido por la carga puntual ubicada en el origen de coordenadas):
E = < 0 , k >,
E1 = < 0 , -k/12 > = < 0 , -k >,
y observa que ambas expresiones vectoriales son opuestas, por lo que tienes que el campo resultante es nulo.
Espero haberte ayudado.
-
No lo entiendo y me entra en el examen. Ayuda porfis. Un pelotari golpea con la mano la pelota desde una altura de 1m y con un ángulo de 45º. Sabiendo que el jugador se encuentra a 15 m de la pared del fondo y que la pelota pega con dicha pared a una altura de 3m, determina:
a) La velocidad con la que ha sido lanzada la pelota
b)El tiempo que ha tardado en llegar a la pared
c)La altura máxima
d) El vector velocidad al impactar con la pared
e) El ángulo que forma esta velocidad con la horizontal


Raúl RC
el 23/5/19Hola Sheila, un ejercicio bastante largo de hacerte por aqui, te recomiendo veas previamente los vídeos sobre tiro parabólico, en ellos tienes todas las fórmulas que necesitas, nos cuentas:
Tiro oblicuo o parabólico

Antonio Silvio Palmitano
el 23/5/19Considera un sistema de referencia con origen de coordenadas en el punto de impacto de la mano del pelotari con la pelota, con eje OX paralelo al suelo con sentido positivo hacia la pared del fondo, y con eje OY vertical con sentido positivo hacia arriba.
Luego, tienes los siguientes datos:
xi = 0, yi = 0 (componentes de la posición inicial),
vi = a determinar (rapidez inicial de la pelota),
θ = 45° (ángulo de disparo con respecto a la horizontal),
g = 9,8 m/s2 (módulo de la aceleración gravitatoria terrestre).
Luego, planteas las ecuaciones de posición y de velocidad de Tiro Oblicuo (o Parabólico), reemplazas valores, resuelves coeficientes, cancelas términos nulos, y queda:
x = vi*cos(45°)*t (1)
y = vi*sen(45°)*t - 4,9*t2 (2),
vx = vi*cos(45°) (3),
vy = vi*sen(45°) - 9,8*t (4);
luego, despejas la incógnita t en la ecuación señalada (1), sustituyes en la ecuación señalada (2), resuelves términos, y queda (te dejo la tarea de hacer el desarrollo correspondiente):
y = tan(45°)*x - ( 4,9/(vi2*cos2(45°) )*x2, reemplazas valores, resuelves coeficientes, y queda:
y = x - (9,8/vi2)*x2 (5),
que es la ecuación de la trayectoria de la pelota.
a)
Tienes las coordenadas del punto de impacto de la pelota contra la pared (recuerda que el origen de coordenadas se encuentra a nivel de la mano del pelotari):
x = 15 m, y = 2 m;
luego, reemplazas estos valores en la ecuación señalada (5), y queda:
2 = 15 - (9,8/vi2)*152, restas 15 en ambos miembros, y queda:
-13 = -(9,8/vi2)*152, resuelves el coeficiente en el segundo miembro, y queda
-13 = -2205/vi2, multiplicas por vi2 y divides por -13 en ambos miembros, y queda:
vi2 ≅ 169,615, extraes raíz cuadrada positiva en ambos miembros, y queda:
vi ≅ 13,024 m/s, que es el valor de la rapidez inicial de la pelota.
b)
Sustituyes este último valor remarcado en la ecuación señalada (1), y queda:
x ≅ 13,024*cos(45°)*t, resuelves el coeficiente, y queda:
x ≅ 9,209*t, reemplazas el valor de la abscisa del punto de impacto en la pared (x = 15 m), y queda:
15 ≅ 9,209*t, y de aquí despejas
t ≅ 15/9,209 ≅ 1,629 s, que es el valor del instante de impacto de la pelota contra la pared.
c)
Planteas la condición de altura máxima (la pelota "no sube ni baja"), y queda la ecuación:
vy = 0, sustituyes la expresión señalada (4), y queda:
vi*sen(45°) - 9,8*t = 0, reemplazas el valor de la rapidez inicial, resuelves el primer término, y queda:
9,209 - 9,8*t ≅ 0, y de aquí despejas:
t ≅ 9,209/9,8 ≅ 0,940 s, que es el instante correspondiente a la altura máxima que alcanza la pelota;
luego, reemplazas este valor en la ecuación señalada (2), reemplazas también el valor de la rapidez inicial, y queda:
y ≅ 13,024*sen(45°)*0,940 - 4,9*0,9402, resuelves, y queda:
y ≅ 4,327 m, que es el valor de la altura máxima con respecto al nivel de la mano del pelotari,
por lo que tienes que su valor con respecto al nivel del suelo es: yM ≅ 4,327 + 1 ≅ 5,327 m.
d)
Reemplazas el valor del instante de impacto (t ≅ 1,629 s) en las ecuaciones señaladas (3) (4), reemplazas además el valor de la rapidez inicial de la pelota, y queda:
vx =13,024*cos(45°) ≅ 9,209 m/s,
vy =13,024*sen(45°) - 9,8*1,629 ≅ -6,755 m/s,
que son las componentes de la velocidad de la pelota justo antes de chocar contra la pared,
por lo que la expresión vectorial de esta velocidad queda: vimp ≅ < 9,209 , -6,755 > (en m/s).
e)
Planteas la expresión de la tangente del ángulo determinado por la velocidad con respecto a la horizontal justo antes del impacto, y queda:
tan(θimp) = vy/vx, reemplazas valores, y queda:
tan(θimp) ≅ -6,755/9,209, resuelves, y queda:
tan(θimp) ≅ -0,734, compones en ambos miembros con la función inversa de la tangente, y queda:
θimp ≅ -36,261°, que es el valor de la medida del ángulo determinado por la velocidad de impacto y la horizontal.
Espero haberte ayudado.