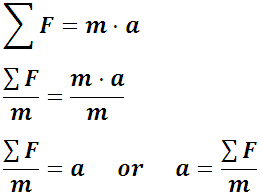Foro de preguntas y respuestas de Física

Nybhrum
el 2/6/19

Mecaniza los ejercicios, tras practicar mucho llega un momento en el que te das cuenta de que en cada tema hay ciertas variaciones y todos los ejercicios en torno a el son iguales, claro... esto lleva bastante tiempo y dedicacion xD.

Pedro
el 2/6/19

Estoy de acuerdo contigo Nybhrum, es una de las cosas que estoy intentando hacer, pero "solamente" tengo las tardes y muchas de ellas entre tareas del hogar, o que llego reventado de mi curre (recuerdo que es un trabajo físico) no hago todo lo que me gustaría. En mates me resulta muy fácil mecanizar, en física me está costando más.

Nybhrum
el 2/6/19

Si ese es el caso, creo que lo ideal seria que mirases los temas y que los ejercicios que tardes mas de x tiempo, los plantees aqui para que alguien te horiente con formas de verlos. Luego no te estreses si ves que no haces muchos ejercicios, yo hay dias que he estado 4 horas para hacer menos de 10 ejercicios pero que si para el dia siguiente lo tienes aprendido, merece totalmente la pena. Es mejor entender los conceptos desde el principio que ir tirando poco a poco con detalles que se acumulan al final.

Un mes es bastante tiempo, si te esfuerzas desde hoy lo puedes sacar con notaza

Pedro
el 2/6/19

No, no, está claro, el ponerme nervioso es malo.

Hay días que me puedo hacer fácilmente 100 ejercicios de un mismo tema, luego hay días que intento LOS MISMOS ejercicios y no me salen ni 20 por que vengo agobiado del trabajo, noto que se me echa el tiempo encima o mil historias. Así que bueno, poco a poco, paciencia y no hay más.

Adela
el 2/6/19

Hola, tengo un problema que no logro entender. Podríais explicarmelo.

Una carrera ciclista consta de dos etapas en línea y una contrarreloj. La primera etapa en línea es de 220km y se rueda a una velocidad media de 40km, la segunda etapa tarda en recorrerse 3h y 25min a una velocidad media de 36km. La tercera es de 20km y se recorre de media a 30km. Determina la distancia total que recorren los ciclistas, el tiempo total empleado y la velocidad media de todo el recorrido.

Antonio Silvio Palmitano
el 2/6/19

Tienes los datos de la primera etapa:

d₁ = 220 Km (distancia que recorren los ciclistas),

v₁ = 40 Km/h (rapidez media de los ciclistas),

t₁ = a determinar (tiempo empleado por los ciclistas en esta etapa);

luego, planteas la expresión del intervalo de tiempo en función de la distancia y de la rapidez media, y queda:

t₁ = d₁/v₁ = 220/40 = 11/2 h.

Tienes los datos de la segunda etapa:

d₂ = a determinar (distancia que recorren los ciclistas),

v₂ = 36 Km/h (rapidez media de los ciclistas),

t₂ = 3 h 25 min = 3 + 25/60 = 3 + 5/12 = 41/12 h (tiempo empleado por los ciclistas en esta etapa);

luego, planteas la expresión de la distancia en función del tiempo y de la rapidez media, y queda:

d₂ = v₂*t₂ = 36*(41/12) = 3*41 = 123 Km.

Tienes los datos de la tercera etapa:

d₃ = 20 Km (distancia que recorren los ciclistas),

v₃ = 30 Km/h (rapidez media de los ciclistas),

t₃ = a determinar (tiempo empleado por los ciclistas en esta etapa);

luego, planteas la expresión del intervalo de tiempo en función de la distancia y de la rapidez media, y queda:

t₃ = d₃/v₃ = 20/30 = 2/3 h.

a)

Planteas la expresión de la distancia total recorrida por los ciclistas, y queda:

d = d₁ + d₂ + d₃ = 220 + 123 + 20 = 363 Km.

b)

Planteas la expresión del tiempo total empleado por los ciclistas, y queda:

t = t₁ + t₂ + t₃ = 11/2 + 41/12 + 2/3 = (66 + 41 + 8)/12 = 115/12 h = 9 + 7/12 = 9 + 35/60 = 9 h 35 min.

c)

Planteas la expresión de la rapidez media de los ciclistas para toda la carrera, y queda:

v = d/t = 363/(115/12) = 363*12/115 = 4356/115 Km/h ≅ 37,878 Km/h.

Espero haberte ayudado.

Claudia Rivero
el 2/6/19

Se trata de este problema:

Gracias!

Pd: no he encontrado el video que trata este tema, si me pueden poner el link si esta o algo lo agradecería mucho🤗

Antonio Silvio Palmitano
el 2/6/19

Tienes la expresión vectorial de la velocidad del móvil en función del tiempo:

v(t) = < 8t² , -6t² > (1) (en m/s),

cuyo módulo queda expresado:

│v(t)│ = √( (8t²)² + (-6t²)² ) = √( 64t⁴ + 36t⁴ ) = √( 100t⁴ ) = 10t² (2) (en m/s);

de donde tienes que el vector unitario correspondiente a la dirección de la velocidad, que es el vector tangente a la trayectoria del móvil, queda expresado:

T(t) = v(t) / │v(t)│, aquí sustituyes las expresiones señaladas (1) (2), y queda:

T(t) = < 8t² , -6t² > / 10t² = < 0,8 , -0,6 > (3) (observa que en este caso la expresión es abstracta, o sea, sin unidades de medida).

Luego, derivas con respecto al tiempo en la ecuación señalada (1), y la expresión de la aceleración del móvil queda:

a(t) = < 16t , -12t > (4) (en m/s²).

Luego, planteas la expresión de la componente tangencial de la aceleración, y queda:

a_T(t) = a(t) • T(t), sustituyes las expresiones señaladas (4) (3), y queda:

a_T(t) = < 16t , -12t > • < 0,8 , -0,6 >, desarrollas el producto escalar en el segundo miembro, y queda:

a_T(t) = 16t*0,8 - 12t*(-0,6), resuelves términos, y queda:

a_T(t) = 12,8t + 7,2t, resuelves, y queda:

a_T(t) = 20t (5) (en m/s²).

Luego, evalúas las expresiones señaladas (4) (5) para el instante en estudio (t = 2 s), y queda:

a(2) = < 32 , -24 >, cuyo módulo queda expresado:

│a(2)│ = √( 32² + (-24)² ) = √( 1024 + 576 ) = √( 1600 ) = 40 m/s² (5), que es el valor del módulo de la aceleración del móvil;

a_T(2) = 20(2) = 40 m/s², que es la componente tangencial de la aceleración en el instante en estudio, cuyo módulo es: │a_T(2)│ = 40 m/s² (6).

Luego, planteas la expresión del módulo de la aceleración del móvil en función de los módulos de sus componentes (observa que la componente tangencial y la componente normal son perpendiculares, por lo que planteamos una ecuación pitagórica), y queda:

a_N(2)² + a_T(2)² = a(2)², reemplazas el valor señalado (5) y el valor remarcado y señalado (6), y queda:

a_N(2)² + 40² = 40², y de aquí despejas: a_N(2) = 0.

Espero haberte ayudado.

•2 voto/s•

alex
el 2/6/19

Hola unicoos tengo una duda y no soy capaz de resolverla espero que alguien pueda.

en la parte de la "E" deformada la "E" que saignifica?????

Gracias

Claudia Rivero
el 2/6/19

No es una E deformada, se trata de el simbolo de sumatorio, representado con la letra griega sigma mayuscula, y se refiere a sumar todas las fuerzas que actuan sobre un cuerpo en el eje que estes estudiando, que seguramente sea el x

•2 voto/s•

Y3
el 2/6/19

Qué pasa si en el examen me confundo y saco el tiempo con la segunda formula?? Alguien me explica cuándo debo usar una u otra para saber el tiempo?? Muchas gracias!!!!!

Francisco Javier
el 2/6/19

No es cuestión de cuál debes usar, es cuestión de en cuál de las dos tengas la mayor cantidad de información o datos. Siempre debes usar la formula en donde solo tengas una incógnita. Si tienes dos incógnitas en una ecuación no puedes obtener nada. Por lo general en estos problemas siempre habrá solo un camino inicial; usar solo una formula y en base a lo calculado allí poder usar las demás. En este caso fíjate que inicialmente no puedes usar la segunda fórmula que pones, ya que no conoces ni "y" ni "t". Y es obvio que debes fijarte en otra fórmula que no sea esta; otro camino inicial.

Al fijarte en la primera fórmula vez que conoces todo menos "t". Así que este sería el camino correcto.

Carlos Perez
el 1/6/19

Muchas gracias Nybhrum, pero sigo sin comprenderlo. Según el ejemplo que se suele poner, una bola colocada en una cama elástica crea una depresión en la misma ("curva" el espacio próximo), de tal forma que un objeto que rueda por la cama y llega a la depresión, sigue la línea curvada por la bola y se acerca a ésta; ahora bien, si colocamos ese objeto, inmóvil, en el borde de la depresión, para que "caiga" en la misma necesitamos una fuerza que lo atraiga (o lo empuje). Es decir, que la curvatura del espacio que propugna la teoría de la relatividad no permitiría prescindir de las fuerzas clásicas de Newton, a mi simple entender.

Nybhrum
el 2/6/19

No hay una "fuerza de atraccion", es simplemente el cuerpo afectado por la modificacion del espacio que necesita desplazarse. Imaginate que sigues una trayectoria recta y derrepente entras en un agujero, no puedes simplemente ignorarlo y seguir en la misma coordenada "altura", tienes que desplazarte en la altura para seguir tocando la coordenada "suelo" y seguir con la trayectoria original.

Puedes "intentar" evadir el cambiar la altura, modificando la trayectoria o el espacio mismo, pero en el momento en el que hagas eso, dejarias de seguir un "moviento natural", es decir, es alto que has hecho por tu voluntad, no se si me explico xD.

Lo que quiero decir es, todo cuerpo esta vinculado a una posicion en los ejes de coordenadas, si un cuerpo modifica el espacio, no puedes simplemente ignorar las modificaciones y "levitar", tu trayectoria se adapta al nuevo terreno por naturaleza.

Carlos Perez
el 1/6/19

Según la relatividad la fuerza gravitatoria está causada por una masa que curva el espacio alrededor, desviando las trayectorias de los objetos móviles que pasan cerca; pero por qué, si ponemos un objeto inmóvil cerca de una masa, dicho objeto debería empezar a moverse, según esa teoría. ¿Alguien podría aclarármelo por favor?

Nybhrum
el 1/6/19

En Teoria, todas las masas modifican el espacio, lo "curvan" y por ello, los cuerpos cercanos pueden tender a acercarse a este cuerpo que genera la deformacion.

Ahora, si la masa que tienes es minuscula, este "efecto" se puede despreciar. El modificar el espacio al rededor solamente es apreciable por cuerpos celestes con gran masa.

mery
el 1/6/19

Hola buenas tardes, de el siguiente ejercicio no me sale la velocidad de escape ya que en el solucionario me pone que la velocidad de escape es de 6,14x10⁴

La distancia media del planeta Júpiter al Sol es 5.203 veces la distancia media de la Tierra al Sol. La masa de Júpiter es 317,8 veces la masa de la Tierra, y Tiene un radio que es 10,52 veces el radio terrestre. Supongamos que las órbitas de los planetas que giran alrededor del Sol son circulares. Calcule:

a) La duración del «año» de Júpiter, es decir, el tiempo que tarda Júpiter a hacer unavolta torno al Sol.

b) La velocidad de escape a la superficie de Júpiter.

DATOS: Rterra = 6 367 km; g = 9,80 m / s

Francisco Javier
el 2/6/19

Supongo que ya sabes calcular el inciso a). Así que te ayudo solo con el inciso b).

Planteamos la energía mecánica de dos objetos cuando están separados una distancia:

E = 0.5*m*v² - (G*M*m)/r

Donde "m" es la masa de un objeto cualquiera y "M" la masa del planeta (Júpiter en este caso).

Llamando "A" al punto en la superficie de Júpiter y "B" al punto de altura máxima tenemos que:

E_A = 0.5*m*v_A² - (G*M_Júpiter*m)/r_A

E_B = 0.5*m*v_B² - (G*M_Júpiter*m)/r_B

En el punto "A":

v_A = v_escape

r_A = R_Júpiter

En el punto "B":

v_B = 0

r_B = R_Júpier + h = r_máximo

Reemplazando en las expresiones de energía mecánica:

E_A = 0.5*m*v_espape² - (G*M_Júpiter*m)/R_Júpiter

E_B = - (G*M_Júpiter*m)/r_máximo

Como la energía se conserva, podemos decir que:

E_A = E_B

0.5*m*v_espape² - (G*M_Júpiter*m)/R_Júpiter = - (G*M_Júpiter*m)/r_máximo

Despejando para "v_escape":

v_escape² = (2*G*M_Júpiter)/R_Júpiter - (2*G*M_Júpiter)/r_máximo

v_escape² = 2*G*M_Júpiter*(1/R_Júpiter - 1/r_máximo)

Como queremos que la masa "m" llegue alcanzar la mayor distancia posible para escapar, tenemos la condición que:

r_máximo → ∞

Significa que:

1/r_máximo = 1/∞ = 0

Entonces:

v_escape² = 2*G*M_Júpiter*(1/R_Júpiter)

v_escape = [2*G*M_Júpiter*(1/R_Júpiter)]^0.5

Del enunciado:

M_Júpiter = 317.8*M_Tierra

De tablas: M_Tierra = 5.98x10²⁴ kg

Entonces:

M_Júpiter = 317.8*5.98x10²⁴ = 1.9004x10²⁷ kg

También se menciona en el enunciado que:

R_Júpiter = 10.52*R_Tierra

Como dato del problema: R_Tierra = 6367 km*(1000 m/1 km) = 6.367x10⁶ m

Entonces:

R_Júpiter = 10.52*6.367x10⁶ = 6.6981x10⁷ m

Finalmente, reemplazando todos estos datos en la expresión de la velocidad de escape damos con la respuesta.

Recuerda que G = 6.67x10^-11 N*m²/kg²

v_escape = [2*G*M_Júpiter*(1/R_Júpiter)]^0.5

v_escape = [2*6.67x10^-11*1.9004x10²⁷*(1/6.6981x10⁷)]^0.5

v_escape = 6.1521x10⁴ m/s

Sara
el 1/6/19

¿Alguien me puede ayudar con este ejercicio por favor?

Berthin Alexander
el 1/6/19

Usuario eliminado
el 1/6/19

Porfavor necesito ayuda ,gracias!!

Francisco Javier
el 1/6/19

Asignamos como punto "A" al lugar donde el vagón esta justo antes de chocar con el primer resorte.

Asignamos como punto "B" al lugar donde el vagón se detiene por acción de los dos resortes.

Calculamos la energía mecánica en "A", sabiendo que allí solo habrá energía cinética "K".

Recordamos que:

K = 0.5*m*v²

Entonces:

E_A = K_A = 0.5*m*v_A² = 0.5*6000*v_A²

E_A = 3000*v_A²

Calculamos la energía mecánica en "B", sabiendo que allí solo habrá energía potencial elástica "U_e".

Recordamos que:

U_e = 0.5*k*x²

Hay que tener en cuenta que en este punto habrá dos magnitudes de energía elástica.

Una que proporciona el primer resorte "U_e(k1)" y otra que proporciona el segundo resorte "U_e(k2)".

El valor de "x" para estas energías cambian. Del enunciado es fácil distinguir que:

x_(k1) = 50 cm

x_(k2) = 50 - 30 = 20 cm

Pasando estas distancias a unidades acordes al sistema internacional (SI):

x_(k1) = 50 cm*(1 m/100 cm) = 0.5 m

x_(k2) = 20 cm*(1 m/100 cm) = 0.2 m

Dicho esto:

E_B = U_e(k1) + U_e(k2) = 0.5*k₁*x_(k1)² + 0.5*k₂*x_(k2)² = 0.5*1600*0.5² + 0.5*3400*0.2²

E_B = 268 J

Y ahora aplicando conservación de energía entre los puntos "A" y "B" (ya que no hay fuerza de rozamiento).

E_A = E_B

3000*v_A² = 268

Y de aca se despeja "v_A" para la respuesta.

v_A² = 268/3000 = 0.0893

v_A = (0.0893)^0.5

v_A = 0.2988 m/s