-
Problema de la vida real:
Tenemos que crear un calendario para las rotaciones mensuales que va a realizar un grupo de 6 PERSONAS, POR PAREJAS, en TRES PUESTOS DE TRABAJO. Es decir, cada mes una pareja estará trabajando en cada uno de los tres puestos de trabajo.
Deben cumplirse las siguientes condiciones:
- Todos tienen que cambiar de puesto de trabajo cada mes
- Todos tienen que cambiar de pareja cada mes.
- Al cabo de un tiempo, las seis personas habrán tenido que trabajar el mismo número de veces en cada uno de los tres puestos de trabajo.
- Al cabo de un tiempo las parejas deberán haberse repetido el mismo número de veces. No puede haber parejas que se formen mas veces que otras.
Saludos!


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola buen dia , solo ocupo que alguien me de una idea de como utilizar las derivadas en el sig problema por que no veo como se relaciona :) gracias
Tienes que llevar agua por una loma con una manguera de 1´´ y las especificaciones de la bomba dicen que su capacidad es para 4 metros en vertical y la loma que sube es semejante a la funcion x2+5x+4 donde primero cae 2 metros y luego sube 6 metros - ¿tiene capacidad la bomba?


Breaking Vlad
el 10/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Me pueden a ayudar con esto? entiendo que este centrada en el (0, 0) pero no entiendo como llega a que sea raiz de k-1. Lo he intentado por mi cuenta y bueno he llegado a la opción D, pero no es correcta, gracias.
Las curvas de nivel k ≥ 1de la funcion
son:
Circunferencia de radio ... centradas en ...


Jose Ramos
el 7/2/20La respuesta es la C. Para obtener las curvas de nivel para k≥1, hay que resolver x2 + y2 +1 = k, de donde x2 +y2 = k -1 (Como k≥1, k -1 ≥0) y x2+y2 = k-1 es la ecuación de una circunferencia de centro (0,0) y radio √k-1 (La ecuación de una circunferencia de centro (a, b) y radio r es: (x-a)2 + (y-b)2 = r2)
-
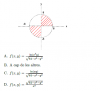
Alguien me puede ayudar a entender estas funciones, dudo entre la A y la C, no entiendo como diferenciarlas... Gracias.
Dada la siguiente representación gráfica del dominio de f, a que función corresponde?


Jose Ramos
el 7/2/20Es la C. puesto que ln(x2.y) no comprende el tercer cuadrante ya que en dicho cuadrante y es negativa y por tanto x2y < 0, con lo cual no estaría definido el logaritmo.
Por tanto la respuesta correcta es la C donde xy >0 tanto en el primero (x>0 e y>0, xy>0), como en el tercer cuadrante (x<0 e y <0, xy>0)
Si haces que lo que hay dentro de la raíz en el denominador sea mayor que cero, obtienes los puntos del círculo de centro (0,0) y radio 8 (x2+y2-64≤0, implica x2 +y2 ≤ 64)
-
Buen día a todos, estoy realizando un trabajo de investigación acerca de logística urbana en mi ciudad y el tipo de muestreo que se ha manejando es POR CONVENIENCIA. Mis preguntas son:
1. El muestreo por conveniencia debe ser específicamente debe ser de un enfoque?, o puede ser mixto? (cuantitativa y cualitativo)
2. Cómo se calcula el tamaño de muestra en una muestreo por conveniencia? o estos no se calculan?
3. En el muestro por conveniencia puedo usar herramientas de recolección de datos como encuestas y entrevistas o por métodos de observación?
-
Hola a todos. Tengo un problema y me gustaría ver si a ustedes se les ocurre una solución.
Mi problema es el siguiente: Tengo 3000 frases en una matriz y quiero que cada día me de una frase de esas 3000, que no haya salido antes y que no sea correlativa.
$frases = [1,2,3,4,5,6...3000];
$hoy = 20200207; // Formato Año-Mes-Dia
Con estos dos datos, uno fijo que son la cantidad de frases y otro dinámico que es el día, me gustaría saber si a alguien se le ocurre alguna fórmula para que cada día me de una frase distinta (un numero de 1 a 3000) y que ese número
no sea correlativo. Es decir si ayer entregue la frase 302, hoy no entregue la frase 303. Por otro lado yo puedo tener un $frasesUsada = [2,542,3,654,24] donde guardaría los números de frases ya utilizados.
Muchas gracias !!
-

Sebastian Quintero
el 7/2/20se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)