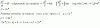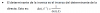-
Hallar la forma binomica de z= 3 ((cos (pi/5)+isin (pi/5))^15. En la forma trigonometrica al usar el teorema de moivre queda -1 la parte real y la imaginaria 0. Por lo tanto el resultado es z=-3. es correcto?.
Y como seria sin calculadora,el calculo del coseno y del seno?.
-


Antonio Silvio Palmitano
el 31/1/20Te mostramos formas alternativas, en las que "preparamos" las expresiones de las funciones, para luego derivar.
a)
Tienes la expresión de la función, cuyo dominio es: D = R:
y = (e2x + ex)/e-x, aplicas la propiedad de las potencias con exponente negativo, y queda:
y = (e2x + ex)*ex, distribuyes, y queda:
y = e2x*ex + ex*ex, resuelves las multiplicaciones de potencias con bases iguales en los términos, y queda:
y = e3x + e2x;
luego, derivas término a término (observa que debes aplicar la Regla de la Cadena, y queda:
y' = e3x*3 + e2x*2, ordenas factores en los términos, y queda:
y' = 3*e3x + 2*e2x,
y observa que la función derivada está definida en todo el dominio de la función.
b)
Tienes la expresión de la función, cuyo dominio es: D = (0;+∞):
y = Ln[√(x)], aplicas la propiedad de las potencias con exponentes fraccionarios, y queda:
y = Ln(x1/2), aplicas la propiedad del logaritmo de una potencia, y queda:
y = (1/2)*Ln(x);
luego, derivas, y queda:
y' = (1/2)*(1/x), resuelves la multiplicación de expresiones fraccionarias, y queda:
y' = 1/(2*x),
y observa que la función derivada está definida en todo el dominio de la función.
Espero haberte ayudado.
-
Determinar si el siguiente subconjunto es o no subespacio vectorial de Pn, es decir, del espacio des los polinomios de grado más pequeño o igual que n:
p(t) = a + t 2 , donde a ∈ R.