-
Decid a cuál de las diferentes interpretaciones de la probabilidad corresponde la afirmación siguiente:
Si lanzamos un dado muchas veces, por término medio, en uno de cada seis lanzamientos obtenemos un 4, y por eso la probabilidad de obtener 4 al lanzar un dado es de uno sexto. -
lím √2x+8 -(2)
x→-2 ∛4x +(2)
¡Hola chicos, buenas tardes! espero se encuentren bien, hoy necesito su ayuda con este ejercicio:( si pudieran ayudarme sería de mucha ayuda, gracias..
-
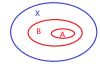
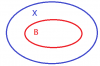
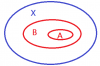
Sean A,B subconjuntos de X y sea F={x∈X:x∈A→x∈B}. Demuestra F=(X\A)∪B.
-
Hola, después de hallar los límites de integración, he calculado el área que comprenden estas dos funciones, pero me da un resultado muy raro y no se si está bien. Los límites de integración son de 0 a 1. Gracias por la ayuda
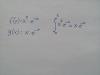


Antonio Silvio Palmitano
el 17/7/17Los límites de integración son correctos, pero si tienes que calcular el área de la región limitada por las gráficas de ambas funciones, observa que la función g toma valores mayores que los que toma la función f en el intervalo (0,1), por lo que el área queda expresada:
A = ∫ (x*e-x - x2*e-x)*dx = ∫ (x - x2)*e-x*dx, para evaluar con Regla de Barrow entre x = 0 y x = 1 (1).
Observa que la integral se resuelve con el método de integración por partes en dos pasos (planteamos la integral indefinida):
I = ∫ (x - x2)*e-x*dx,
u = x - x2, de donde tienes: du = (1 - 2x)*dx
dv = e-x*dx,de donde tienes: v = - e-x;
luego aplicas el método y la integral queda:
I = - (x - x2)*e-x + ∫ (1 - 2x)*e-x*dx;
luego, vuelves a aplicar el método para resolver la integral secundaria:
u = 1 - 2x, de donde tienes: du = - 2dx
dv = e-x, de donde tienes: v = - e-x;
I = - (x - x2)*e-x - (1 - 2x)*e-x - 2*∫ e-x*dx,
resuelves la última integral y queda:
I = - (x - x2)*e-x - (1 - 2x)*e-x + 2*e-x + C.
Luego, sustituyes en la ecuación señalada (1) y queda:
A = [ - (x - x2)*e-x - (1 - 2x)*e-x + 2*e-x ],
aplicas la Regla de Barrow y queda:
A = (0 + e-1 + 2*e-1) - (0 - 1 + 2) = 3*e-1 - 1 = 3*e-1 - 1 = 3/e - 1 = (3 - e)/e.
Espero haberte ayudado.
-
No entiendo la resolución del ejercicio 18 apartado b). No se porque se va la ec. de a.
http://calculo.cc/temas/temas_geometria_analitica/vectores_espacio/problemas/vectores_espacio.html


Antonius Benedictus
el 17/7/17Cuando sumas miembro a miembro la segunda y la tercera ecuación, te queda b+c=0, de donde c=-b.
La primer ecuación queda a= una combinación lineal de parámetros libres, o sea un valor libre.
Entonces, un vector que satisfaga lo pedido es cualquier vector de la forma (a, b, -b), donde la a y la b pueden tomar cualquier valor y la tercera coordenada es el valor opuesto de la 2ª.
La confirmación de que este vector depende linealmente de v_1 y v_2 nos la da el hecho de que el determinante formado por los tres vectores vale 0. Esto es, el rango de la correspondiente matriz cuadrad es <=2.