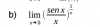-
Nando Hull
el 24/6/17Hola como analizar la continuidad de esta funcion Y=Ln(9-x^2) necesito ayuda su Dom=(-3;3)..
-
Maria Eugenia Maisano
el 24/6/17 -
Jose Castillo Lam
el 24/6/17
Hola, cómo están? Espero que me puedan ayudar resolviendo este proyecto de Matemáticas. Se los agradecería mucho. Saludos
Antonius Benedictus
el 24/6/17
Antonius Benedictus
el 24/6/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Nicolas Ramirez
el 24/6/17Holaa,espero que me puedan ayudar con este problema de optimizacion
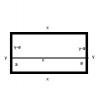
Se intenta cercar un campo rectangular con 4 hebras de alambre y despues subdividir el campo en dos partes con una cerca paralela a uno de los lados,utilizando 2 hebras de alambre.
se dispone de 600 mts de alambre,Determine las dimensiones del terreno de area maxima
Antonio Silvio Palmitano
el 24/6/17
Observa que debes emplear cuatro hebras de alambre para completar el perímetro (P = 2x + 2y),
por lo que la longitud de alambre necesaria es: C1 = 4*(2x + 2y) = 8x + 8y.
Observa que debes emplear dos hebras de alambre para completar la base intermedia (bi = x),
por lo que la cantidad de alambre necesaria es: C2 = 2x.
Luego, puedes plantear para la cantidad total de alambre:
C1 + C2 = 600 m, sustituyes expresiones y queda:
8x + 8y + 2x = 600, reduces términos semejantes y queda:
10x + 8y = 600, haces pasaje de término y queda:
8y = 600 - 10x, divides en todos los términos por 8 y queda:
y = 75 - (5/4)*x (1),
observa que y expresa una longitud, por lo que debe ser estrictamente positiva, por lo que puedes plantear:
75 - (5/4)*x > 0, multiplicas en todos los términos de la inecuación por 4 y queda:
300 - 5*x > 0, divides en todos los términos de la inecuación por - 5 (observa que cambia la desigualdad) y queda:
- 60 + x < 0, haces pasaje de término y queda:
x < 60, luego observa que x expresa una longitud, por lo que debe ser estrictamente positiva, por lo que tienes la condición:
0 < x < 60.
Luego, puedes plantear para el área total:
A(x,y) = x*y, sustituyes la expresión señalada (1) y queda:
A(x) = x*(75 - (5/4)*x, distribuyes y queda:
A(x) = 75*x - (5/4)*x2 (2)., que es la expresión de la función área, cuyo dominio es: D = (0,60).
Luego, plantea las expresiones de las derivadas primera y segunda:
A ' (x) = 75 - (5/2)*x,
A ' ' (x) = - 5/2.
Luego, plantea la condición de punto crítico (posible máximo o posible mínimo):
A ' (x) = 0, sustituyes en el primer miembro y queda:
75 - (5/2)*x = 0, multiplicas en todos los términos de la ecuación por 2/5 y queda:
30 - x = 0, haces pasaje de término y queda: 30 m = x,
y observa que la derivada segunda es negativa para este valor, por lo que la gráfica de la función presenta un máximo.
Luego reemplazas en las expresiones señaladas (1) (2) y queda:
y = 75 - (5/4)*30 = 75 - 75/2 = 75/2 m = 37,5 m;
A = 30*75/2 = 1125 m2.
Espero haberte ayudado.
-
Daniel Macchiavello
el 24/6/17 -
Martín Ramírez
el 24/6/17 -
Emanuel Ruiz
el 24/6/17 -
Heide Solorzano
el 24/6/17 -
Anderson Calet Ramriez
el 24/6/17si dos puntos colineales se encuentran separados por una cuerda de doce metros, si desde el punto medio elevamos la cuerda a una altura de 2 metros ¿cuanto de longitud agregariamos a la cuerda para que los puntos sigan separados por doce metros?
Antonio
el 24/6/17Haz el dibujo.
En un principio tienes un segmento de 12 m de longitud,
pero luego, tienes:
un triángulo con 12 m de base y 2 m de altura, la cual lo divide en dos triángulos rectángulos idénticos con catetos 6 y 2 metros.
halla la hipotenusa de uno de ellos, la multiplicas por dos y obtienes la longitud de la nueva cuerda
solo tienes que ver cuánto sobrepasa a 12
Sol: 0.65 m
-
Nico
el 24/6/17
