Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Álvaro
el 19/6/17

Dada una función, por ejemplo, y = 6/x, ¿sería posible hallar la expresión de todas sus rectas tangentes en función de x?

••0 voto/s
•
César
el 19/6/17
f(x)=6/x f´(x)=-6/x^2 Ec. tangente y-f(a)=-f´(a)(x-a)

•0 voto/s
•

Cancelar
Daniel
el 19/6/17

Buenas tardes me podéis ayudar con este ejercicio
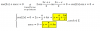
√50 -3/2 √27+√64 -2/5 √ 12+√98.
creo que se hace sacando factor común pero no estoy seguro
gracias tengo recuperación mañana

••0 voto/s
•
César
el 19/6/17
Usa parentesis Daniel asi nos resulta imposible.

•1 voto/s
•
Juan Lladó
el 19/6/17
teniendo en cuenta que:
50 = 2*5*5
64 = 2*2*2*2*2
12 = 2*2*3
27 = 3*3*3
98 = 2*7*7
entonces:
5√2 -9/2 √3 + 4√2 - 4/5√3 + 7√2
16√2 -53/10√3

•1 voto/s
•

Cancelar
Paula Sánchez
el 19/6/17

Hola! No encuentro el fallo pero tampoco se seguir, podrían ayudarme?

••0 voto/s
•
César
el 19/6/17
será valida siempre que cos(2a)≠0

•0 voto/s
•
Paula Sánchez
el 19/6/17
No entiendo el paso que has realizado, el ejercicio se supone que tiene que dar 1

•0 voto/s
•

Cancelar
stefany
el 19/6/17

Podéis Ayudarme a resolver esta derivada, gracias
e^x-2+1

••0 voto/s
•
Antonio Silvio Palmitano
el 19/6/17
Observa que puedes separar en términos, y que en el primer término debes aplicar la regla de la cadena, luego la expresión de la función derivada queda:
f ' (x) = e^x-2* (1 - 0) + 0 = e^x-2.
Espero haberte ayudado.

•0 voto/s
•

Cancelar
Paula Sánchez
el 19/6/17

como se resuelve esta ecuación?
cos 3x + cosx = 0

••0 voto/s
•
Guillem De La Calle Vicente
el 19/6/17

•0 voto/s
•
Antonius Benedictus
el 19/6/17
Mejor así:

•0 voto/s
•

Cancelar
Paula Sánchez
el 19/6/17

como se resuelve esta ecuación?
senx - √3 x cosx = 0

he visto todos los videos y en ninguno viene de ese tipo

••0 voto/s
•
Antonio Silvio Palmitano
el 19/6/17
Observa que no se trata de una ecuación trigonométrica, ya que el primer factor del segundo término es polinómico.
En este tipo de ecuaciones se emplean otros métodos, que son para aproximar soluciones.
De todas formas, observa que x = 0 es una solución de esta ecuación, ya que reemplazas y queda:
sen0 - √(3)*0*cos0 = 0 - 0 = 0.
Espero haberte ayudado.

•0 voto/s
•
Antonius Benedictus
el 19/6/17
Pon foto del enunciado original, Paula.

•0 voto/s
•
Paula Sánchez
el 19/6/17
Es la única foto que puedo poner ya que está sacada de un examen de unicoos

•0 voto/s
•
Guillem De La Calle Vicente
el 19/6/17

•0 voto/s
•

Cancelar
Facu Imfeld
el 19/6/17

Hola, algún unicoo universitario me podría indicar cuál es mi error en este ejercicio?
Dada la función g(x,y) = x ² + y ² + 1
Calcular mediante el gradiente, la derivada direccional en el punto P(1,2) con dirección del punto Q(2,3)
Derivo parcialmente la función respecto a x y obtengo:
ag/ax = 2x
Derivo parcialmente la función respecto a y y obtengo:
ag/ay = 2y
Evalúo P en las derivadas parciales y obtengo el gradiente
grad = (2,4)
Para obtener la derivada direccional en el punto dado, debo saber el módulo del vector PQ
PQ = (2-1;3-2) = (1,1)
|PQ| = √(1)^2+(1)^2 = √2
En definitiva, la derivada direccional en el punto es el producto del gradiente evaluado en P por el vector unitario de PQ (denotado como U)
U = (1/ √2; 1/ √2)
Du(x,y) = (2,4).(1/ √2; 1/ √2) = (2/√2) + (4/√2) = 6/√2
Tengo la duda de si 6/√2 es el resultado correcto, porque el solucionario del libro tiene 3/√2 como respuesta, y la verdad es que no encuentro en todo lo que hice, algún posible error. Muchas gracias de antemano!

••0 voto/s
•
Antonio Silvio Palmitano
el 19/6/17
Has planteado y resuelto correctamente el ejercicio, solo te faltó indicar que la función g es diferenciable en R², por lo que es diferenciable en un entorno del punto P.
Luego, observa tu resultado:
6/√(2) = 6*√(2) / ( √(2) )² = 6*√(2) / 2 = 3*√(2), que es una expresión equivalente.
Es probable que se trate de un error de impresión en tu solucionario.
Espero haberte ayudado.

•0 voto/s
•
Facu Imfeld
el 19/6/17
Muchas gracias Antonio!

•0 voto/s
•

Cancelar
María José
el 19/6/17

Buenos días, acabo de registrarme como usuaria PRO, ¿cúal es el material adicional a parte de los videos? Muchas gracias y un saludo a tod@s.

••0 voto/s
•
Antonius Benedictus
el 19/6/17
Lo tienes debajo de cada vídeo en el icono "material adicional".

•1 voto/s
•
María José
el 19/6/17
Muchas gracias por responder con tanta rapidez. Un saludo.

•0 voto/s
•

Cancelar
Carlos Gallego Madrigal
el 19/6/17

Alguien sabe cual es la falsa?
La b y la d creo que son verdaderas. Un saludo.

••0 voto/s
•
Antonius Benedictus
el 19/6/17
La c es la falsa, pues si las funciones son continuas , se cumple la igualdad.

•1 voto/s
•

Cancelar
Steven Buzón Ávila
el 19/6/17

a) Calcular la masa de un rombo de vértices (0,0), (1,0), (1,1) y (2,1) sabiendo que su densidad en cada punto (x,y) viene dada por la función d(x,y)= x^2 + y + 1
b) Calcular el centro geométrico del rombo.

••0 voto/s
•
Antonius Benedictus
el 19/6/17
¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

•0 voto/s
•
Antonio Silvio Palmitano
el 19/6/17
Vamos con una orientación.
a)
Puedes trazar las gráficas de la recta paralela al eje OY cuya ecuación es x = 1,
y tendrás que ésta divide al paralelogramo en dos triángulos:
R₁: limitado por las rectas cuyas ecuaciones son y = 0, y = x, x = 1;
R₂ limitado por las rectas cuyas ecuaciones son: y = 1, y = x-1, x = 1.
Luego, puedes plantear:
M = M₁ + M₂,
donde tienes:
M₁ = ∫∫ (x² + y + 1)*dy*dx, con 0 ≤ y ≤ x, 0 ≤ x ≤ 1;
M₂ = ∫∫ (x² + y + 1)*dy*dx, con x-1 ≤ y ≤ 1, 1 ≤ x ≤ 2;
y queda que hagas los cálculos y termines la tarea.
b)
Recuerda que el punto de intersección entre las diagonales de un paralelogramo es su centro geométrico.
Tienes para las diagonales:
d₁, que pasa por los puntos (1,0) y (1,1), que está incluida en la recta de ecuación x = 1,
d₂, que pasa por los puntos (0,0) y (2,1), que está incluida en la recta de ecuación y = (1/2)x.
Luego, queda que resuelvas el sistema de ecuaciones, y tendrás que su solución es C(1,1/2).
Espero haberte ayudado.

•0 voto/s
•
Guillem De La Calle Vicente
el 19/6/17
a) Adjunto un esquema
Por definición la masa de un elemento infinitesimal del rombo: dm=d dx dy
La masa del rombo será:
m=∫∫d dx dy                      (con límite inferior de la primera integral "rombo")
Integrando primero respecto a x y luego respecto a y se tiene:
m=∫dy∫(x²+y+1)dx              (primera integral definida de 0 a 1 y segunda de y a y+1)
b) Hay que precisar si se desea conocer el centro de masa o el centro geométrico, son puntos diferentes por lo general y únicamente coinciden cuando la densidad es uniforme.
Para el centro de masa (x_c,y_c) se tendrá:
Momento estático respecto al eje y=m y_c
Momento estático respecto al eje x=m x_c
Entonces por definición de momento estático se tiene:
∫∫yd dx dy=my_c          (limite inferior de la primera integral "rombo")
∫∫xd dx dy=mx_c          (límite inferior de la primera integral "rombo")
Ambos integrales se pueden calcular de forma semejante a como se obtuvo la masa, es decir con los mismos límites de integración. Luego despejas y_c,x_c..
$y_{c}, x_{c}$
Para el caso del centro geométrico lo mejor es tomar d(x,y)=1 en lugar de m tendrás el área

•0 voto/s
•

Cancelar