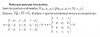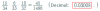-
Marta
el 13/6/17 -
Marta
el 13/6/17
Alguien puede ayudarme con el 2?
Jordan Chillo
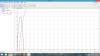
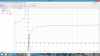
el 13/6/17
b) (90t-240)(/t+4) debido a que t=24 tomas la segunda función por el dominio, y reemplazas
(90*24-240)/(24+4)=68,57142857
c) 40= (90t-240)/(t+4)
40t+160=90t-240
-50t=-400
t=8
d) No debido a que la asíndota horizontal es 90 es decir 90% de ocupación, por lo que no nunca llegara a 100% con valores positivos
-
Mr Crakero
el 13/6/17Alguien puede ayudarme hacer a calcular la matriz hessiana de f(x,y)=x^y. Se que hay que hacerla primera derivada respecto a x y luego a y, y luego hacer la segunda derivada de xx, xy, yx e yy. Pero con esta matriz f(x,y)= x^y me esta siendo complicada resolverla. ¿Alguien podria echarme una mano?
Antonio Silvio Palmitano
el 13/6/17f(x,y) = xy = (elnx)y = eylnx, cuyo dominio es: D = { (x,y) ∈ R2 / x > 0 }.
Luego, las expresiones de las derivadas parciales primeras quedan:
fx = eylnx*y/x
fy = eylnx*lnx
Luego, las expresiones de las derivadas parciales segundas quedan.
fxx = eylnx*y2/x2 - eylnx*y/x2 = eylnx*y*(y - 1)/x2,
fxy = eylnx*lnx*y/x + eylnx/x = eylnx*(y*lnx + 1)/x,
fyx = eylnx*(y/x)*lnx + eylnx/x = eylnx*(y*lnx + 1),
fyy = eylnx*(lnx)2.
Luego, puedes plantear la condición de punto estacionario:
fx: eylnx*y/x = 0
fy: eylnx*lnx = 0
Haces pasajes de los factores exponenciales (observa que son estrictamente positivos) como divisores y queda:
y/x = 0
lnx = 0, aquí compones con la función inversa del logaritmo natural y queda:
x = e0 = 1,
luego reemplazas en la primera ecuación y queda: y/1 = 0, haces pasaje de divisor como factor y queda:
y = 0;
por lo que la gráfica de la función presenta un único punto estacionario: A(1,0).
Luego, reemplazas en las expresiones de las derivadas parciales segundas y queda (te dejo los cálculos):
fxx(1,0)= 0,
fxy(1,0) = 1,
fyx(1,0) = 1,
fyy(1,0) = 0.
Luego, la matriz Hessiana correspondiente al punto estacionario queda:
H(1,0) =
0 1
1 0
Luego, su determinante queda:
|H(1,0)| = 0*0 - 1*1 = - 1 < 0,
por lo que, según el criterio de las derivadas segundas, tienes que la gráfica de la función presenta:
ensilladura en A(1,0), y el valor de la función en dicho punto es: f(1,0) = 10 = 1.
Espero haberte ayudado.
-
Cristian Sanchez Garcia
el 13/6/17Buenos dias necesito ayuda con este ejercicio de ecuacion en el plano ya que no se que hago mal ya que el resultado no me da
Antonio
el 13/6/17Al estar la recta r contenida en el plano pedido los puntos de la misma están en el plano, por lo que el punto que tienes que coger para la ecuación del plano es un punto cualquiera de la recta r y no, como has hecho, un punto de la otra recta, la recta s.
Por otro lado necesitas dos vectores paralelos al plano pedido, como ambas rectas son paralelas al mismo, obtenemos un vector de cada una de ellas:
- el vector de r es (1,-1,-3) como está en la hoja de ejercicios y no el que estás usando
- el vector de s es (-2,3,-4) como está en la hoja pero no está en el determinante, ahí tienes (2,3,4)
Sería la opción b
-
Periko
el 13/6/17 -
Jaime Cuevas López
el 13/6/17Buenas tardes,
No se como solucionar un apartado que me dice que dé la variedad afín L que generan 3 puntos. Si alguien puede explicármelo con un ejemplo,se lo agradezco.
Gracias de antemano¡
Saludos
-
Carlos Gallego Madrigal
el 13/6/17 -
Carlos Gallego Madrigal
el 13/6/17Alguien que me diga si he resuelto bien el ejercicio? o si no como se haria? Gracias
Ángel
el 13/6/17
Carlos Gallego Madrigal
el 13/6/17
Ángel
el 13/6/17 -
David
el 13/6/17Buenos días, ¿podríais ayudarme con el siguiente ejercicio?, no se que razonamiento se sigue para llegar a la solución marcada en amarillo:
Me imagino que uno de los pasos es dividir la integral en dos integrales, una de [0,1] y la otra de [1,2], ya que el valor del primer intervalo nos lo dan, el segundo no se como obtenerlo.
Un saludo, gracias.
Antonio Silvio Palmitano
el 13/6/17Puedes plantear la sustitución (cambio de variable):
x = 2w, de donde tienes: dx = 2dw
y también tienes: x/2 = w, y observa que para x = 0 corresponde w = 0, y que para x = 2 corresponde w = 1.
Luego, pasas a la integral (para evaluar x entre 0 y 2):
I = ∫ f(x) dx = sustituyes = ∫ f(2w) 2dw = 2 ∫ f(2w) dw = aplicas la última ecuación el enunciado y queda:
= 2 ∫ (f(w) + 1) dw =
= 2 ∫ f(w) dw + 2 ∫ 1 dw = 2 ∫ f(w) dw + [ 2w ] =
observa que evaluamos para w entre 0 y 1, por lo que la integral del primer término es igual a 1,
luego reemplazas y queda:
= 2*1 + (2*1 - 2*0) = 2 + (2 - 0) = 2 + 2 = 4.
Espero haberte ayudado.
David
el 13/6/17Gracias por la ayuda, llevo un rato mirándolo, la verdad es que no termino de entender el razonamiento, me pierdo un poco con los límites de integración.
Si no es molestia, me gustaría consultarte otra duda , en la parte "= 2 ∫ f(w) dw + 2 ∫ 1 dw = 2 ∫ f(w) dw + [ 2w ] =" , ¿por qué evalúas entre 0 y 1?
Un saludo, gracias.
-
Ángel
el 13/6/17San Antonio de Padua nació en Lisboa el 1195 y murió en Padua el 1231. Quiso la Providencia que al emprender viaje para ir a las misiones, una tormenta lo llevase junto a San Francisco de Asís, que le destinó a estudiar primero, y luego a enseñar en la universidad y a predicar. Como dicen sus biógrafos, tuvo el mérito de saber hermanar la acción con la contemplación. Fue profesor, orador sagrado, fundador de hermandades y cofradías, enfermero solícito, teólogo eminente, hombre de gobierno y humilde cocinero, todo casi a un mismo tiempo. Se le atribuyen innumerables prodigios, por lo que se le llama también el Taumaturgo de Padua. Se le suele representar con el niño Jesús en brazos a causa de que se le apareció repetidamente. Dejó varios tratados de ascética y se han publicado también sus sermones. Una institución vinculada a él es la del Pan de los pobres. Su fiesta se celebra el 13 de junio.
¡¡ Feliz onomástica a los tres Antonios !! :D
