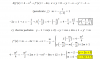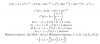logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • icon

    Luis Andrés Mariño
    el 2/6/17


    Antonio¿ hiciste primero determinantes 3x3 para la ampliada (todos dan cero)  antes del 2x2?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Te lo he explicado al final de tu entrada anterior. No hace falta hacer todos los menores de orden 3.



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Alvaro
    el 2/6/17

    Buenas unicoos el apartado b y c,¿como se harian?, se que habria que sacar un sistema de ecuaciones, pero no se por que no me salen correctamente, gracias de antemano

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Luis Andrés Mariño
    el 2/6/17

    Si el rango de una matriz 3x3 vale 1, y todos los determinantes 3x3 de la ampliada son = 0, el rango de la ampliada también vale 1,¿no?  

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Pon el enunciado original y te lo explicamos, Andrés.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonius Benedictus
    el 2/6/17

    Cuando sometemos a una matriz a transformaciones elementales, se obtienen matrices equivalentes, esto es, que tienen el mismo rango.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Alvaro
    el 2/6/17

    si el rango de una matriz 3x3 vale 1, entonces el R(A)= 3 y por tanto el R(A')=3 ya que la matriz (A) pertenece a la A'

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Luis Andrés Mariño
    el 2/6/17

    ¿Por qué hiciste un determinante 2x2 para el rango de la ampliada? ¿No se hace primero determinantes 3x3 con la columna de términos independientes y ver si alguno da distinto de cero? 

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
    icon

    Luis Andrés Mariño
    el 2/6/17

    No os entiendo perdonad. ¿No se hacen determinantes 3x3 con la ampliada hasta que uno de distinto de 0? En este caso dan todos 0. Luego, ¿haces determinantes 2x2?

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
    icon

    Luis Andrés Mariño
    el 2/6/17

    La ampliada vale 1 o 2, no 3. 

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    nada
    icon

    Antonius Benedictus
    el 2/6/17

    El rango de una matriz es también el máximo numero de filas (y de columnas) linealmente independientes. Al haber una fila de 0 en A', su rango ya no puede ser 3. 

    Si manejas bien los conceptos y las propiedades de matrices y de determinantes, excusas de hacer tantos cálculos.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
  • icon

    fernando
    el 2/6/17

    1/4 (4x+2) + 1/6 (3-6x)=1


    lo que se hace es por ejemplo en la primera fraccion multiplicar el 1 por el 4x y el 4 por el +2?  Es que lo hice asi, y no me dio bien el resultado.


    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Fernando: pon foto del enunciado original, pues me temo que la ecuación esté mal transcrita.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Ángel
    el 2/6/17

    Lo correcto es multiplicar TODO el numerador y TODO el denominador (si no tiene denominador, de manera implícita este va a valer uno, pero "no se pone")

    tienes que multiplicar el 1 por (4x+2)

    y el 4 por 1 (que aunque el 1 no se vea, está en el numerador dividiendo a (4x+2)


    O está mal transcrita o se obtiene un resultado raro, que nos confirme Fernando...

    1/4*(4x+2) + 1/6* (3-6x)=1

    (4x+2)/4 + (3-6x)/6 = 1

    (24x+12)/24 + (12-24x)/24 = 24/24

    (24x+12) + (12-24x) = 24

    24x+12+12-24x = 24

    24=24

    Por lo que podríamos concluir que x tiene infinitas soluciones (puede tomar cualquier valor en los números reales). 

    El resultado 24=24 nos muestra que el resultado de la ecuación es verdadero independientemente del valor de x (pues no aparece)


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    fernando
    el 2/6/17


    La foto me ha salido un poco borrosa, si hace falta hago otra, sorry

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Sara Tarjuelo
    el 2/6/17

    Buenos días, podríais ayudarme con este ejercicio? Gracias

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Crecimiento y curvatura

    Visiona estos vídeos e intenta hacer algo y nos lo muestras.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Adrian Alvarez Rodriguez
    el 2/6/17

    Buenas tardes, podrian ayudarme a resolver el ejercicio 1? Un saludo y gracias.  

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Revisa as operacións aritméticas, Adrián.

    Que teñas moita sorte na selectividade.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Cristina Iglesias
    el 2/6/17

    3. Halla el punto simétrico de P(0,2,1) respecto al plano π: x+y-z=2


    Me dan números altísimos

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17

    Muéstranos tus resultados, Cristina.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Antonio Silvio Palmitano
    el 2/6/17

    Llamemos Q(a,b,c) al punto buscado.

    Observa que el vector normal al plano es: n = < 1 ,1 , -1 >,

    y que él es el vector director de la recta perpendicular al plano (r), que pasa por el punto P(0,2,1),

    cuyas ecuaciones cartesianas paramétricas quedan:

    x = 0 + t

    y = 2 + t

    z = 1 - t

    t ∈ R

    Luego, planteamos la intersección entre la recta r y el plano, y para ello sustituimos las expresiones de las ecuaciones paramétricas de r en la ecuación del plano y queda:

    t + 2 + t - (1 - t) = 2, de donde despejamos: t = 1/3,

    luego reemplazamos en las ecuaciones cartesianas parmétricas y queda: x = 1/3, y = 7/3, z = 2/3,

    por lo que tenemos que la recta y el plano se cortan en el punto M(1/3,7/3,2/3).

    Por último, planteamos que el punto M es el punto medio entre los puntos P y Q, por lo que tenemos que las coordenadas del punto M son iguales a los promedios entre las coordenadas de los puntos P y Q:

    (a + 0)/2 = 1/3, de donde despejamos: a = 2/3,

    (b + 2)/2 = 7/3, de donde despejamos: b = 8/3,

    (c + 1)/2 = 2/3, de donde despejamos: c = 1/3,

    por lo que tenemos que el punto buscado tiene coordenadas: Q(2/3,8/3,1/3),

    y observa que el punto Q pertenece a la recta perpendicular al plano que pasa por los punto P y M.

    Espero haberte ayudado.

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
  • icon

    Cristina Iglesias
    el 2/6/17

    3. Halla el punto simétrico de P(0,2,1) respecto al plano π: x+y-z=2

    4.determina la ecuación de un plano π paralelo al plano de ecuación 2x-y+z+4=0 que dista 10 unidades del punto (2,0,1)

    Estos dos necesito saber si los hice bien porque no me deja subir la foto

    reply•thumb_up•0 voto/s•flag
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Antonius Benedictus
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    suficiente
    icon

    Cristina Iglesias
    el 2/6/17

    Muchas gracias Antonio Benito tenia mal la ecuación

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Heide Solorzano
    el 2/6/17

    Heyyy Chicos, buenas noches

    Quisiera que me ayuden con el dominio y el rango de estas 3 funciones, he intentado realizaras 

    f(x)=e^x-1 ----- en esta lo que hice fue pasar e a un logaritmo natural y simplificar para que me de uno pero no se que mas hacer

    f(x)= x+sen(x)----Esta no tengo ni idea de como realizar intente con métodos algebraicos pero no logro dar con el dominio

    f(x)= ln(x)-2 ------ intente pasarla a euler pero no se si estará bien por que me sale la respuesta 1 (cosa que no se cual es mi dominio si ese fuera el resultado)


    Les agradezco mucho, espero y puedan ayudarme, puesto que he estado practicando mucho para una lección que tengo de calculo mañana por la mañana.

    Muchas gracias 

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 2/6/17

    Dominio.

    f(x)=e^x-1 ℛ

    f(x)= ln(x)-2  ]0,∞[


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Heide Solorzano
    el 2/6/17

       Muchas gracias

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    Ángel
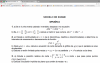
    el 2/6/17

    f(x)=e^(x-1)    

    -------

    Dom=ℛ -----------> La función tiene un valor para todas y cada una de las x pertenecientes a los reales desde -inf a inf

    -------

    Para hallar el rango tenemos que obtener x de f(x)=y sustituir después las y por x (obtendremos la función inversa)

    El rango es el dominio de esa función inversa

    ln(y)= lne^(x-1)  

    lny=(x-1)*lne

    lny=x-1

    x=lny+1

    f-1(x)= lnx+1

    Dom f-1(x)= Rango f(x)= (0,inf)        

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Ángel
    el 2/6/17

    f(x)= x+sen(x)

    --------

    Dom=ℛ ----------->  Esta función no da ningún problema de dominio para ningún valor, pues es una suma de funciones polinómica y trigonométrica (por definición su dominio es (-inf,inf). Observa que cualquier valor que demos a x tiene una imagen en I

    El rango es desde [-1,1]

    -----------------------------------------------------------------------

    f(x)= ln(x)-2


    Dominio= (0,inf)

    Rango=ℛ


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Pablo Molina
    el 2/6/17


    Ayuda con la integral

    reply•thumb_up•0 voto/s•flag
    icon

    Axel Morales Piñón.
    el 2/6/17


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante