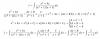-
Marta
el 17/5/17Hola, alguien me podria hacer estas derivadas porfavor, yo ya las hice pero creo q las tengo mal. Gracias de antemano ❤
Axel Morales Piñón.
el 17/5/17 -
Guillem De La Calle Vicente
el 17/5/17
Existencia de solución de EDO en toda la línea real.
Considera la EDO
y'=f(t,y), y(a)=b
Quiero saber las condiciones en f o en la solución para que la solución existe en toda la línea real ℛ. Sólo sé que son los siguientes
- Si la solución es monótona y limitada entonces la solución existe en toda la línea real.
- Si f es globalmente Lipschitz en ℛ × ℛ entonces la solución existe en toda la línea real.
Por favor, sugerir en otro tipo de propiedades o dar algunas referencias. Muchas gracias .
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Guillem De La Calle Vicente
el 17/5/17Demuestra por reducción al absurdo que para todo n∈ℕ, si n es senar entonces (n+1)² es par.
Rubén
el 17/5/17Hola, Guillem
Por reducción al absurdo, supongamos que n es impar y que (n+1)2 es impar. Al ser impares, para ciertos m y l enteros, n = 2l - 1 y (n+1)2 = 2·m - 1. Por lo tanto, tenemos que ( 2l - 1 + 1 )2 = 2m - 1 -> ( 2l )2 = 2m - 1 -> 4l2= 2m - 1 con lo que llegamos a una contradicción ya que a un lado tenemos un número par y al otro lado un número impar. De aquí se extrae que si n es impar, (n+1)2 es necesariamente par.
Espero haber ayudado!
-
Dana Darchuk
el 17/5/17Una pelota de golf sigue un movimiento uniformemente acelerado y su altura viene dada por la formula h=2/5t-1/250t^2 Sabiendo que el tiempo esta dado en segundos y la altura en metros: a)Dibuja la grafica b)que altura maxima alcanza? c)A que longitud llega?
-
MARI JOSE
el 17/5/17 -
Jair Bruzzone
el 17/5/17
Para poder responder el enunciado debería graficar la funcion, pero me encuentro trabado en la primera.
Si mal no entiendo debo obtener las asintotas V y H, pero al momento de igual a 0 la funcion nose como manejar el -3x. Disculpen las molestias y muchas gracias
Isaac Naveira Comesaña
el 17/5/17Hola Jair , para que esas funciones de tipo racional sean continuas basta con saber en que puntos se anula el denominador de la funcion :
Por ejemplo
a) x-2=0 ---> x=2 no está en el dominio de la funcion puesto que te quedaria 1/0 - 3*2
b) x+2=0 -----> x=-2 no esta en el dominio ya que se anula el denominador
c) x^2-4x+3=0 -----> lo resolvemos con la formula de las ecuaciones de segundo grado y nos queda que x=3 o x=1
Espero haberte ayudado ! un saludo
César
el 17/5/17 -
Eli
el 17/5/17 -
Guillem De La Calle Vicente
el 17/5/17Sean m, n, r números naturales estrictamente positivos. Demuestra por reducción al absurdo que si tenemos m · n + r objetos y los distribuimos entre m cajas, entonces por fuerza hay al menos una caja que tiene más de n objetos.
Rubén
el 17/5/17Hola, Guillem
Por reducción al absurdo, supongamos que no existe ninguna caja que tenga más de n objetos. Por lo tanto entre todas las m cajas podrán haber, a lo sumo, m·n objetos. Lo cual es una contradicción ya que tenemos m·n + r donde r es natural >0. La contradicción viene de suponer, evidentemente, que todas las cajas tienen como mucho n objetos ( Esto no deja de ser el principio del palomar ).
Espero haber ayudado!
-
Guillem De La Calle Vicente
el 17/5/17Los dos riegos de abajo tienen áreas de base iguales. Sus chorros están abiertos. ¿Cuál de las dos latas puede contener un mayor volumen de agua en las posiciones verticales?
Isaac Naveira Comesaña
el 17/5/17Guillem De La Calle Vicente
el 18/5/17 -
Alex
el 17/5/17Hola, ¿Cómo se resuelve este límite?
lim x2 + x/(x3 -2x2 +x)
x->0
Gracias.
Guillem De La Calle Vicente
el 17/5/17
Axel Morales Piñón.
el 17/5/17
Guillem Figols
el 17/5/17
