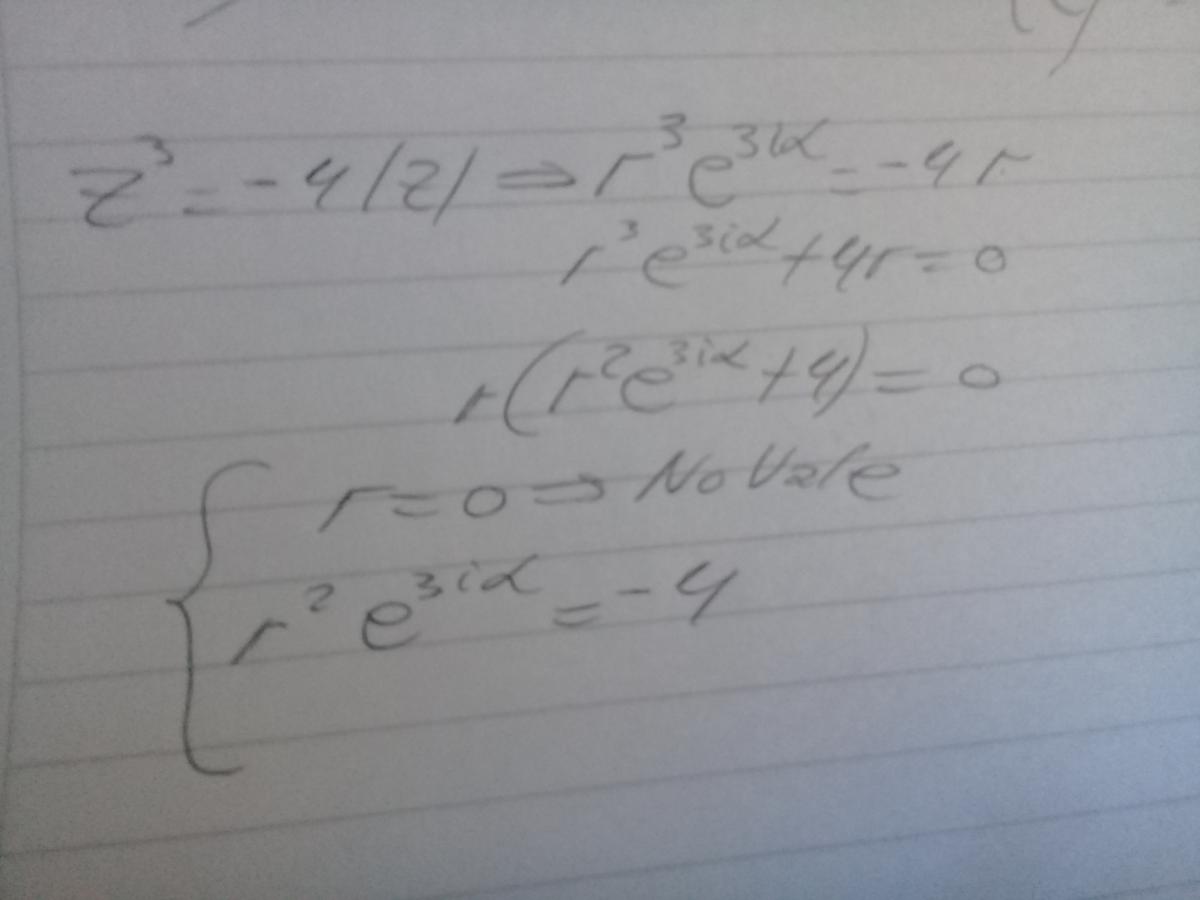-
Para Jose Ramos.
Buenos días Jose. Repito mi pregunta sobre tu contestación a mi duda. Decías: "Si quieres puedes abreviar diciendo los puntos de pentágono {(x,y) ∈ ℕxℕ, tales que "aquí escribes las desigualdades, incluyendo x e y ≥ 0”} “.
Yo comentaba: no sé si te refieres a esto:
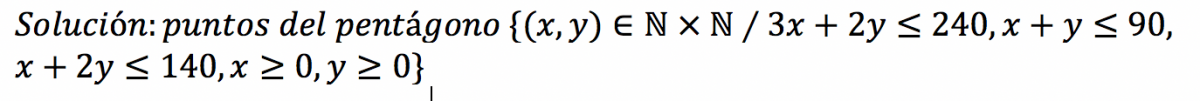
-

gonzalezlbl
el 28/1/20Como x representa el número de años transcurridos desde la fundación, entonces x = 0 es el año de fundación. Así, la cantidad de fundadores viene dado por:
N(0) = 03 - 12 • 02 + 36 • 0 + 20 = 20. Número de socios fundadores = 20.
Por ser un polinomio el dominio sería todos los reales, pero como la cantidad de años comienza a contarse desde x = 0, entonces el dominio = [0 ; +∞)
-


Antonio Silvio Palmitano
el 29/1/20Has hecho correctamente el planteo.
Luego, despejas en la ecuación del módulo, y queda:
r = 7√(4).
Has planteado correctamente la expresión del argumento:
α = (4/9)*π + (2/3)*k*π. y solo te faltó aclarar: k ∈ Z,
y te faltó plantear la condición de argumento principal:
0 ≤ α < 2π, sustituyes la expresión del argumento que has determinado en tu desarrollo, y queda:
0 ≤ (4/9)*π + (2/3)*k*π < 2π, multiplicas por 9 y divides por π en todos los términos de esta inecuación doble, y queda:
0 ≤ 4 + 6*k < 18, restas 4 en los tres miembros de esta inecuación doble, y queda:
-4 ≤ 6*k < 14, divides por 6 en los tres miembros de esta inecuación doble (observa que no cambian las desigualdades), y queda:
-2/3 ≤ k < 7/3,
por lo que tienes que los argumentos principales corresponden a los valores del parámetro
k: 0, 1 o 2.
Espero haberte ayudado.
-
Buenas, tengo una consulta respecto a escribir conjuntos por extensión.
Los conjuntos son:
F = {x / x ∈ Z; 3 ≤
|x| ≤ 5} no entiendo como es con el valor absolutoH =
{x / x ∈ Z; 1 + x2 = 17} EN ESTE PUSE QUE H ={8}NO se la verdad porque no tengo las rtas para comprobar alguien me explica como seria porfa? gracias
-
En geometría sagrada, el significado del símbolo Metatrón, el ángel de la vida controla el flujo de energía en una figura mística como lo es el Cubo de Metatron, que contiene todas las figuras geométricas de la creación y representa los patrones que componen todo lo que se ha creado.
El cubo de metatron está formado por 13 esferas unidas por líneas desde el centro de cada esfera.
Las esferas del cubo de metatron representan lo ‘Femenino’ y las líneas rectas representan lo ‘Masculino’. Por consiguiente, el Cubo de Metatron completo representa una red de polaridades masculina y femenina para crear el TODO.
La geometría sagrada, se refiere al estudio de formas y fórmulas matemáticas que aparecen en la naturaleza, para más información ir a la nota de geometria sagrada
-