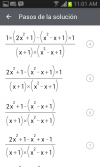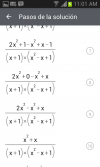Recuerda la expresión para las variaciones sin repetición, para este caso queda:

V(5,x) = 5! / (5 -x)!, luego sustituyes a partir de la ecuación del enunciado y queda:

20 = 5! / (5 -x)!, luego haces pasaje de divisor como factor, resuelves el numerador del segundo miembro y queda:

20*(5 - x)! = 120, divides por 20 en ambos miembros y queda:

(5 - x)! = 6, recuerda que 3! = 6, reemplazas y queda:

(5 - x)! = 3!, comparas argumentos y queda:

5 - x = 3, despejas y llega a:

2 = x.

Espero haberte ayudado.

No me quedo claro esto:

(5 - x)! = 6, recuerda que 3! = 6, reemplazas y queda:

(5 - x)! = 3!. ----------> Lo que hiciste fue reemplazar el 6 por 3!, ya que sabes que es lo mismo, pero si fuera un numero muy grande ¿como haces para aplicar el mismo razonamiento?
                                        -Si conoces un procedimiento que pueda aplicar siempre te lo agradecería.

Gracias por tu tiempo y respuesta.

Si tienes que lidiar con factoriales de números mayores que 10, los deberás dejar expresados. Esta clase de comparación como hemos hecho es viable solo cuando trabajas con factoriales de números naturales menores que 10.

Tienes que ordenar ocho elementos con condiciones:

1) A y H ocupan los extremos, por lo que tienes dos posibilidades: A - - - - - - H y H - - - - - - A, tienes en total: N₁ = 2 posibilidades.

2) B y C están siempre juntos, por lo que tienes diez posibilidades por cada una de las anteriores (recuerda que el primero y el último lugar ya están ocupados):

- B C - - - - -, - - B C - - - -, - - - B C - - -, - - - - B C - -, - - - - - - B C -, y también:

- C B - - - - -, - - C B - - - -, - - - C B - - -, - - - - C B - -, - - - - - - C B -, tienes en total: N₂ = 10 posibilidades.

3) Ordenamos a los demás elementos (D, E. F, G) en los cuatro lugares que todavía es´tan libres, por lo que tienes veinticuatro posibilidades por cada una de las anteriores, tienes en total: N3 = P(4) = 4! = 24 posibilidades.

4) Aplicas el principio de multiplicación y el total queda:

N = N₁*N₂*N₃ = 2*10*24 = 480 posibiidades (maneras) para ordenar a ocho personas con las condiciones que impone el enunciado.

Espero haberte ayudado.

Observa que para las sustituciones que has propuesto, el ángulo θ es el que tiene el vértice "más alto" en tu dibujo del triángulo.

x/2 = secθ, de donde despejaste correctamente: x = 2*secθ, y luego tienes: dx = 2*secθ*tanθ*dθ;

para el factor con la raíz tienes: √(x² - 4)/2 = tanθ, de donde despejas y queda: √(x² - 4) = 2*tanθ.

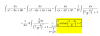
Luego sustituyes y la integral queda:

I = ∫ 8*sec³θ*2*tanθ*2*secθ*tanθ*dθ = 32*∫ tan²θ*sec⁴θ*dθ = 32*∫ tan²θ*sec²θ*sec²θ*dθ = 32*∫ tan²θ*(1 + tan²θ)*sec²θ*dθ,

luego aplicas el método de sustitución (cambio de variable):

w = tanθ, de donde tienes: dw = sec²θ*dθ,

luego sustituyes y la integral queda:

I = 32*∫ w²*(1 + w²)*dw = queda para que continúes con la tarea.

Espero haberte ayudado.

Jous aqui esta... espero a verte ayudado!!

Utiliza el método de Cramer

Te  van los autovalores:

Muchísimas Gracias!