logo_unicoos

Foro de preguntas y respuestas de Matemáticas

logo beUnicoos
Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.
Ir a beUnicoos

  • Usuario eliminado
    el 30/11/16

    Alguien me puede ayudar con este problema, muchas gracias.

    El planteamiento corresponde a una función que determina en un momento dado si una computadora está encendida o apagada, en caso de que esté encendida, la función en ese momento vale 1, y si está apagada toma el valor 0.

    ¿En qué puntos la función es continua y por qué?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 30/11/16

    Llamemos ti a los instantes en que se prende o se apaga la computadora, y observa que ti puede tomar valores reales positivos, ya que consideramos que contamos el tiempo desde t = 0.

    Luego, observa que tenemos intervalos de la forma:

    (0,t1), (t1,t2), (t2,t3),...

    Luego, si consideramos que en el primer intervalo la computadora estuvo apagada tenemos la función cuya expresión a trozos queda:

    f(t) =

    0         si t ∈ (0,t1)

    1         si t ∈ (0,t1)

    0         si t ∈ (t2,t3)

    etcétera

    Luego, observa que los límites laterales para x tendiendo a cada valor ti son distintos. Por ejemplo:

    para t1, el límite por la izquierda es igual a 0, y el límite por la derecha es igual a 1,

    para t2, el límite por la izquierda es igual a 1, y el límite por la derecha es igual a 0,

    y así sucesivamente,

    por lo que tenemos que la función presenta discontinuidades inevitables tipo salto en los puntos ti.

    Por último, tenemos que la función es continua en todos los puntos pertenecientes a los intervalos (que son "internos" en su intervalo correspondiente).

    Espero haberte ayudado.



    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante

    Usuario eliminado
    el 30/11/16

    Muchas gracias.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Franco
    el 30/11/16

    Buenas, quisiera saber como se resuelve esta ecuación diferencial detalladamente:

    xy' + y = x * e^x 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 30/11/16

    Puedes comenzar por dividir por x en todos los términos de la ecuación y queda:

    y ' + (1/x)y = ex,

    luego, observa que se trata de una ecuación diferencial lineal, de primer grado y de primer orden (te recomiendo mires los vídeos sobre este tema), cuya fórmula general es:

    y '+ p(x)y = q(x),

    y cuya solución general es:

    y = e-∫ p(x)dx ( ∫ e∫ p(x)dxq(x)dx + C ) (2).

    Luego, observa que en la ecuación señalada (1) tenemos:

    p(x) = 1/x, y q(x) = ex, luego planteamos:

    ∫ p(x)dx =∫ (1/x)dx = lnx, luego: - ∫ p(x)dx = - lnx = ln(1/x).

    Luego sustituimos en la expresión de la solución general y queda:

    y = eln(1/x) ( ∫ elnxexdx + C ), resolvemos composiciones entre funciones exponenciales y logarítmicas:

    y = (1/x) ( ∫ xexdx + C ), resolvemos la integral del agrupamiento "por partes" y queda:

    y = (1/x) ( xex - ex + C ), distribuimos y llegamos a:

    y = ex - ex/x + C/x.

    Vuelvo a recomendarte mires los vídeos, porque no hemos hecho nada diferente a lo que allí te explican.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Inés
    el 30/11/16

    Por favor alguien puede decirme cómo averiguo x si en una ecuación exponencial me da que 6^x = -1?

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 30/11/16

    Recuerda que las funciones exponenciales de variable real toman siempre valores estrictamente positivos, por lo que si estás trabajando con esta clase de funciones, tienes que la ecuación 6x = -1 no tiene solución:

    Pero si estás trabajando con funciones con variable compleja, allí puedes plantear la igualdad de Euler para el segundo miembro y queda:

    6x = eiπ/2

    tomamos logaritmos naturales en ambos miembros y queda (consideramos valores principales):

    xLn(6) = iπ/2, hacemos pasaje de factor como divisor y queda:

    x =  iπ / 2Ln(6).

    Espero haberte ayudado.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    JONFER
    el 30/11/16
    flagflag

    Hola compañeros, necesito que me ayuden a desarrollar este ejercicio de Ecuaciones Diferenciales, Por favor!




    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 2/12/16

    Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

    Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
  • icon

    Nuria Azores
    el 30/11/16

    Alguien me puede ayudar con este problema de trigonometria de 1ºbach? no se porque pero me lio. Gracias!

    reply•thumb_up•0 voto/s•flag
    icon

    César
    el 30/11/16

    Te dejo una parte , es fácil seguir

    thumb_up•1 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Nuria Azores
    el 30/11/16

    okey gracias! pero como calculo los angulos? no lo veo claro en tu explicacion

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    ¿Te ha ayudado?
    icon

    César
    el 30/11/16

    teorema del seno pues ya conoces los 3 lados y un angulo


    Trigonometria -Teorema del coseno


    Trigonometria- Teorema del seno

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Paula
    el 30/11/16

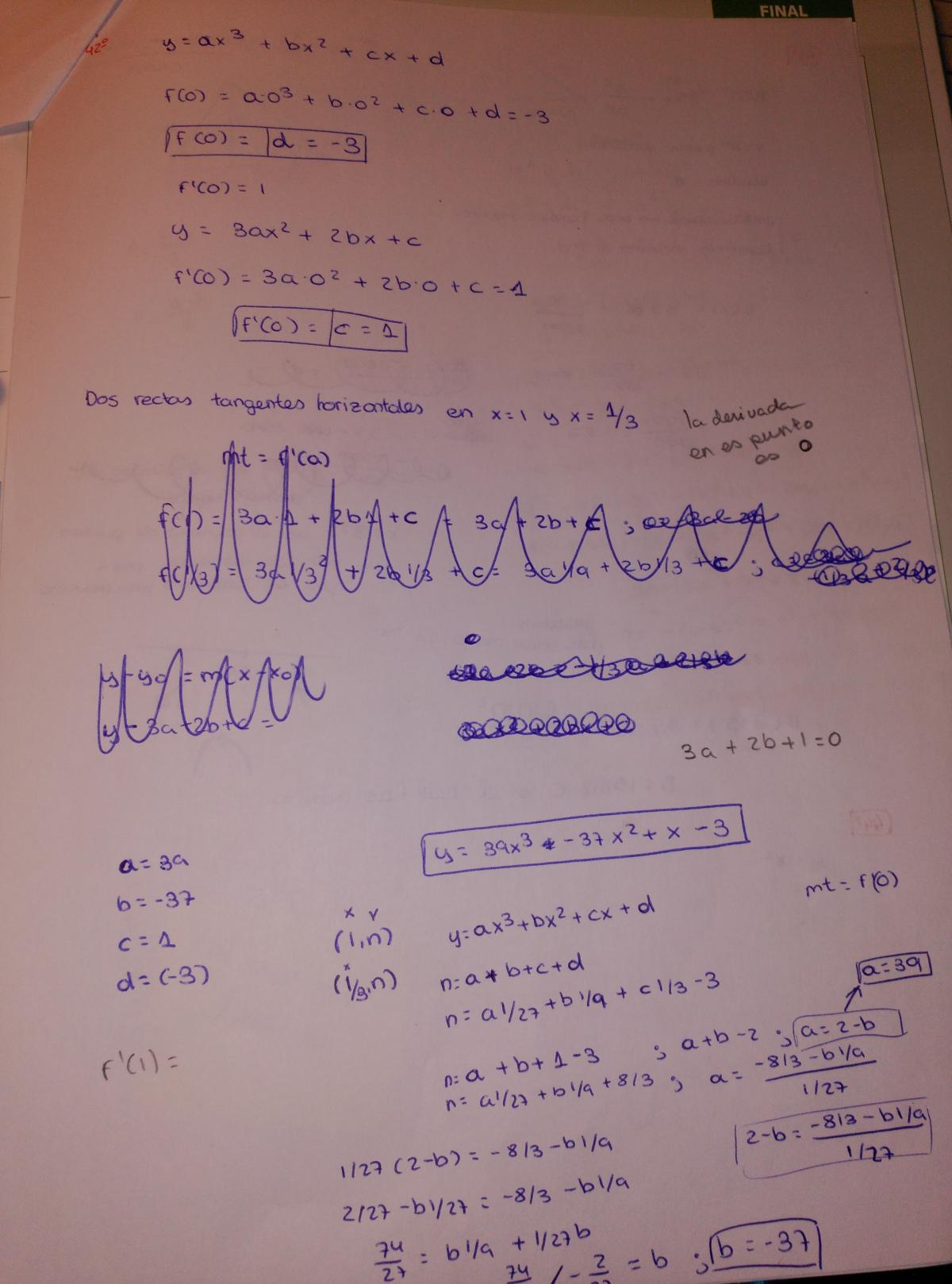
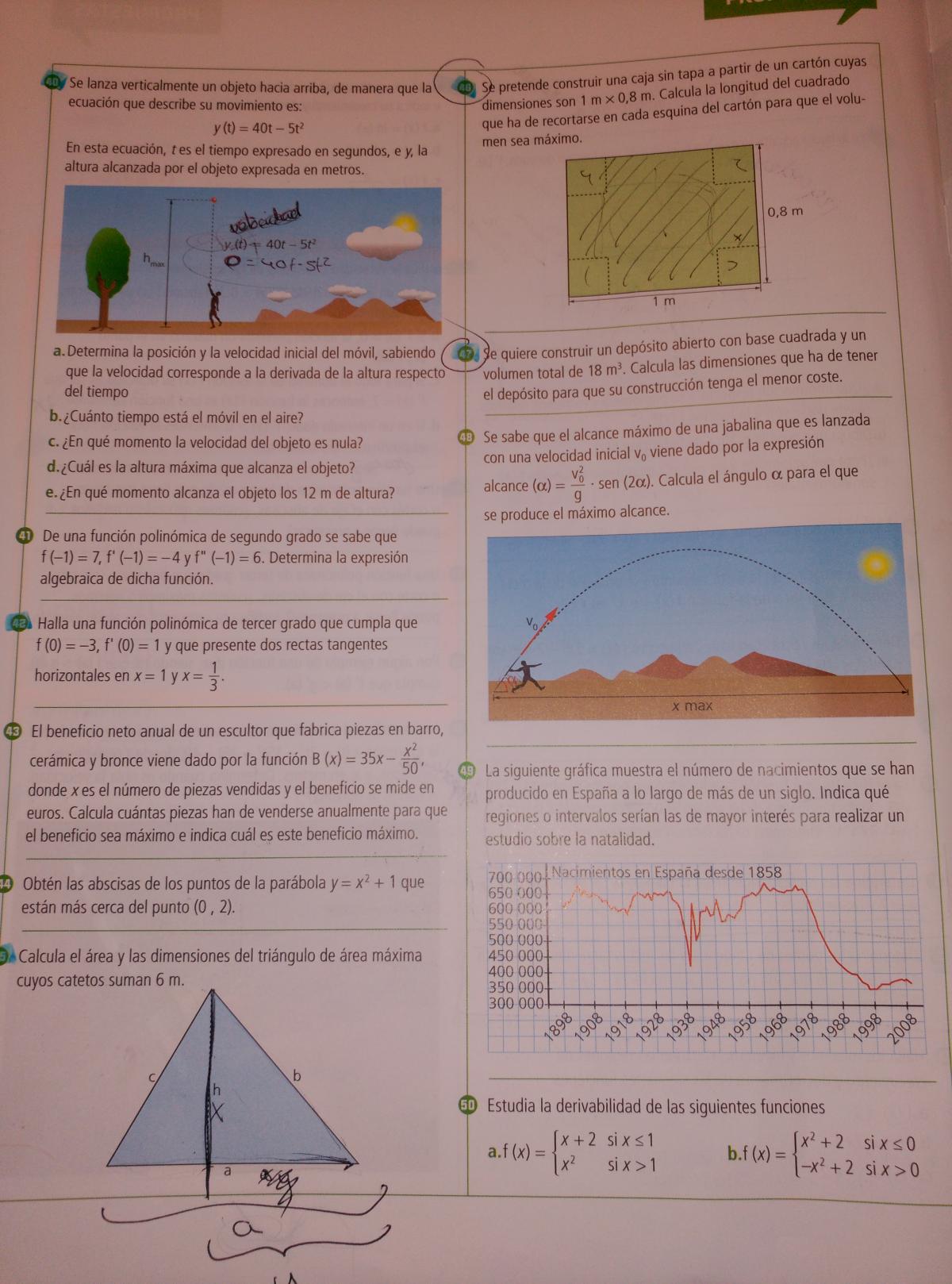
    Hola, tengo examen de problemas relacionados con las derivadas y la optimización no se si los ejercicios enviados están bien o mal y por ejemplo el 42, 44, 45, 46 son en los que mas duda tengo y aunque los he intentado hacer pero no se como seguir. Muchas gracias




    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 2/12/16

    Para la proxima vez, por favor.. Cada ejercicio un post diferente.. Y con fotos más pequeñas... Llevo media hora desplazandome por la pantalla buscando enunciado y solucion correspondiente
    optimiza
    Las abscisas son las coordenadas x de un punto (la x de toda la vida)...
    Para el 44), la distancia entre dos puntos A(a1,a2) y B(b1,b2) es √((a1-b1)²+(a2-b2)²). En tu caso un punto (x,y) perteneciente a la curva y=x²+1 tendrá una distancia al punto (0,2) igual a D=√((x-0)²+(y-2)²)= √(x²+(y-2)²).. Sustituye y por x²+1 en D.... Y deriva la distancia para hallar el máximo.. 

    Para el 45) el area es A=a.h/2... Pero solo tiene sentido hablar de catetos si el triangulo es rectangulo (y el del dibujo no lo es) 
    Para el 46) el volumen de la caja es ALTO x ANCHO x LARGO = V = (1-2x).(0,8-2x).x.. Desarrolla y halla el máximo de esa función...
    Para el 47), revisa este video que es casi identico... Optimización de la superficie de un cilindro (intentalo y nos cuentas)
    Deberías repasar los vídeos de OPTIMIZACION y CRECIMIENTO de UNA FUNCION POLINOMICA, Máximos y minimos de una función, etc...




    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Alberto Universidad
    el 30/11/16

    Buenas, estoy otra vez liado con otro problema de áreas que no me sale.
    Hallar el área encerrada entre y=raiz cuadrada de x, y= -x+6, y=0

    Gracias de antemano


    reply•thumb_up•0 voto/s•flag
    icon

    David
    el 30/11/16

    Echales un vistazo.. Area entre funciones 01

    A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    poco
    icon

    Antonio Silvio Palmitano
    el 30/11/16

    Observa que las dos curvas se cortan en el punto de coordenadas (4,2), que es el vértice superior de la región, cuyos otros dos vértices son los puntos de coordenadas (0,0) y (6,0).

    Luego, observa que si divides en elementos horizontales de área (los visualizas rayando la región con segmentos paralelos al eje OX), verás que por la izquierda tienes a la curva parabólica, cuya ecuación podemos escribir: x = y2, y por la derecha tienes a la recta, cuya ecuación podemos escribir: x = - y + 6.

    Luego, podemos integrar con respecto a y, y el área queda:

    A = ∫ ( (- y + 6) - y2 )dy = ∫ (- y2 - y + 6)dy, para evaluar entre 0 y 2.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Sara92
    el 30/11/16

    otra pregunta (es que las derivadas se me están atragantando) cuando derivo este polinomio  

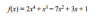
    me sale 8xal cubo - 3x al cuadrado - 14x -3 y ahora tngo que igualarlo a cero, ¿como lo hago?  porque factor común la x no puedo sacar por el tres que esta solo, que tengo que hacer ruffini? 

    reply•thumb_up•0 voto/s•flag
    icon

    Antonio Silvio Palmitano
    el 30/11/16

    Observa que x = 1 es raíz de la función polinómica. Luego su derivada queda:

    f ' (x) = 8x3 + 3x2 - 14x + 3,

    y observa que x = 1 también es raíz de la función derivada (lo que te indica que x = 1 es raíz doble de la función).

    Luego aplicas la Regla de Ruffini y puedes factorizar:

    f ' (x) = (x - 1)(8x2 + 11x - 3).

    Luego, por anulación de un producto, tienes dos opciones:

    a) x - 1 = 0, de donde despejas: x1 = 1;

    b) 8x2 + 11x - 3 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:

    x2 = ( - 11 + √(217 )/16, y también x3 = ( - 11 - √(217 )/16.

    Espero haberte ayudado.


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo
    icon

    Sara92
    el 30/11/16

    Si, me ayudaste muchísimo, porque una vez tenía la derivada no sabía seguir, muchas gracias.

    thumb_up•0 voto/s•flag
    1 2 3 4 5
    muchísimo
  • icon

    Sara92
    el 30/11/16

    Una ayuda con este problema por favor: 

    reply•thumb_up•0 voto/s•flag
    icon

    Fernando Cordoba Espada
    el 30/11/16

    Buenas,  primero simplifica la ecuacion(quita los parentesis) una vez lo tengas, tendras una ecuacion sencillita a la que tienes que hacerle la derivada y se te queda una ecuacion de 2grado que resuelves rapidamente, te dara dos resultados.


    Ahora haz la segunda derivada de la ecuacion principal y sustituyes por separado ambos valores, el maximo sera el que sea menor que 0, y ademas el que mas sentido tiene, sino me equivoco es 21°.


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Fernando Cordoba Espada
    el 30/11/16

    Para el apartado b simplemente sustituye la Temperatura en la primera ecuacion que tte dan y asi tienes la produccion de la hortaliza


    thumb_up•0 voto/s•flag
    1 2 3 4 5
    bastante
    icon

    Antonius Benedictus
    el 30/11/16


    thumb_up•1 voto/s•flag
    1 2 3 4 5
    muchísimo